甘肃省平凉市崆峒区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-09-11 类型:期末考试
一、单选题
-
1. 若代数式 有意义,则实数x的取值范围是( )A、 B、 C、 D、 且2. 下列各组数能作为直角三角形的三边长的是( )A、2,3,4 B、9, , C、 , , D、7, ,3. 下面计算正确的是( )A、 B、 C、 D、4. 下列图象不能表示函数关系的是( )A、
 B、
B、 C、
C、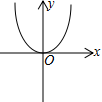 D、
D、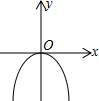 5. 将直线向下平移2个单位长度,所得直线的关系式为( )A、 B、 C、 D、6. 正比例函数的图象在第二、四象限,则一次函数的图象大致是( )A、
5. 将直线向下平移2个单位长度,所得直线的关系式为( )A、 B、 C、 D、6. 正比例函数的图象在第二、四象限,则一次函数的图象大致是( )A、 B、
B、 C、
C、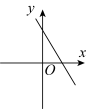 D、
D、 7. 在四边形中, , 分别添加下列条件:①; , 其中能使四边形成为平行四边形的条件有( )A、5个 B、4个 C、3个 D、2个8. 如图,在矩形中,点E在上,且平分 , , , 则的长为( )
7. 在四边形中, , 分别添加下列条件:①; , 其中能使四边形成为平行四边形的条件有( )A、5个 B、4个 C、3个 D、2个8. 如图,在矩形中,点E在上,且平分 , , , 则的长为( )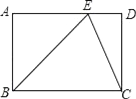 A、 B、 C、 D、9. 如图,函数和的图像交于点P , 根据图像可得不等式的解集是( )
A、 B、 C、 D、9. 如图,函数和的图像交于点P , 根据图像可得不等式的解集是( ) A、 B、 C、 D、10. 如图1,在菱形ABCD中,∠A=60°,动点P从点A出发,沿折线AD→DC→CB方向匀速运动,运动到点B停止.设点P的运动路程为x,△APB的面积为y,y与x的函数图象如图2所示,则AB的长为( )
A、 B、 C、 D、10. 如图1,在菱形ABCD中,∠A=60°,动点P从点A出发,沿折线AD→DC→CB方向匀速运动,运动到点B停止.设点P的运动路程为x,△APB的面积为y,y与x的函数图象如图2所示,则AB的长为( ) A、 B、2 C、3 D、4
A、 B、2 C、3 D、4二、填空题
-
11. 若函数 是正比例函数,则m=.12. 若1、2、、5、7五个数的平均数为4,则x的值是 .13. 在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= .14. 如果直线与两坐标轴所围成的三角形面积是 , 则的值为 .15. 如图,四边形是菱形, , , 于点 , 则 .
 16. 如图,一次函数y=kx1+b1的图象l1与y=kx2+b2的图象l2相交于点P,则方程组 的解是
16. 如图,一次函数y=kx1+b1的图象l1与y=kx2+b2的图象l2相交于点P,则方程组 的解是 17. 如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O , 过点O作OE垂直AC交AD于点E , 则DE的长是 .
17. 如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O , 过点O作OE垂直AC交AD于点E , 则DE的长是 . 18. 正方形 , , …按如图所示放置,点、、…在直线上,点、、…在x轴上,则的坐标是 .
18. 正方形 , , …按如图所示放置,点、、…在直线上,点、、…在x轴上,则的坐标是 .
三、解答题
-
19.(1)、(2)、20. 先化简在求值: ,其中21. 如图,DE是△ABC的中位线,延长DE至F , 使EF=DE , 连接BF .
 (1)、求证:四边形ABFD是平行四边形;(2)、求证:BF=DC .22. “珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次离家距离与所用的时间的关系示意图.
(1)、求证:四边形ABFD是平行四边形;(2)、求证:BF=DC .22. “珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次离家距离与所用的时间的关系示意图.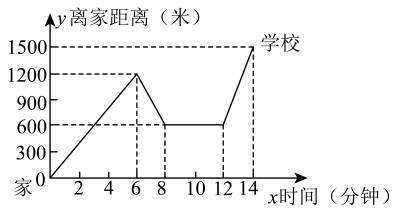
根据图中提供的信息回答下列问题:
(1)、小明家到学校的路程是米;他书店停留了分钟;(2)、本次上学途中,小明骑单车一共行驶了米;(3)、我们认为骑单车的速度超过300米/分钟就超越了安全限度.在整个上学的途中,请通过图像直接判断哪个时间段小明骑车速度最快?然后通过计算说明小明骑单车最快速度是否在安全限度内?23. 如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.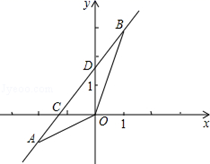 (1)、求一次函数的解析式;(2)、求点C和点D的坐标;(3)、求△AOB的面积.24. 为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2两幅尚不完整的统计图.
(1)、求一次函数的解析式;(2)、求点C和点D的坐标;(3)、求△AOB的面积.24. 为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2两幅尚不完整的统计图.
 (1)、本次抽测的男生有人,抽测成绩的众数是;(2)、请你将图2中的统计图补充完整;(3)、若规定引体向上5次以上(含5次)为体能达标,则该校350名九年级男生中估计有多少人体能达标?25. 在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.求:
(1)、本次抽测的男生有人,抽测成绩的众数是;(2)、请你将图2中的统计图补充完整;(3)、若规定引体向上5次以上(含5次)为体能达标,则该校350名九年级男生中估计有多少人体能达标?25. 在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.求: (1)、用含t的代数式表示Rt△CPQ的面积S;(2)、当t=3秒时,P、Q两点之间的距离是多少?26. “体育承载着国家强盛、民族振兴的梦想,体育强则中国强,国运兴则体育兴.”为引导学生在体育锻炼中享受乐趣、增强体质,某中学准备举办运动会并购进两种体育用品作为运动会奖品.已知购进种体育用品15件和种体育用品20件共需1025元;购进种体育用品10件和种体育用品40件共需1350元.(1)、求两种体育用品的单价;(2)、若购进两种体育用品共80件,且种体育用品的数量不少于种体育用品数量的4倍,请求出最省钱的购买方案.27. 如图1,平面直角坐标系中,直线与x轴交于点 , 与y轴交于点B , 与直线交于点 .
(1)、用含t的代数式表示Rt△CPQ的面积S;(2)、当t=3秒时,P、Q两点之间的距离是多少?26. “体育承载着国家强盛、民族振兴的梦想,体育强则中国强,国运兴则体育兴.”为引导学生在体育锻炼中享受乐趣、增强体质,某中学准备举办运动会并购进两种体育用品作为运动会奖品.已知购进种体育用品15件和种体育用品20件共需1025元;购进种体育用品10件和种体育用品40件共需1350元.(1)、求两种体育用品的单价;(2)、若购进两种体育用品共80件,且种体育用品的数量不少于种体育用品数量的4倍,请求出最省钱的购买方案.27. 如图1,平面直角坐标系中,直线与x轴交于点 , 与y轴交于点B , 与直线交于点 . (1)、求点C的坐标及直线的表达式;(2)、如图2,在(1)的条件下,过点E作直线轴于点E , 交直线于点F , 交直线于点G , 若点E的坐标是 .
(1)、求点C的坐标及直线的表达式;(2)、如图2,在(1)的条件下,过点E作直线轴于点E , 交直线于点F , 交直线于点G , 若点E的坐标是 .①求的面积;
②直线l上是否存在点P , 使的值最小?若存在,直接写出点P的坐标;若不存在,请说明理由.