贵州省黔东南州2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-09-11 类型：期末考试

进入出卷网下载

一、单选题

1. $\sqrt{4}$ 的值为（）

A、 $0$ B、 $1$ C、 $2$ D、 $4$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{8} - \sqrt{3} = \sqrt{5}$ B、 $3 \sqrt{2} - \sqrt{2} = 3$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{12} \div 2 = \sqrt{6}$

查看试题解析
3. 司机王师傅在加油站加油，如图是所用的加油机上的数据显示牌，则其中的常量是（）

A、金额 B、数量 C、单价 D、金额和数量

查看试题解析
4. 甲，乙，丙，丁四人进行射击测试，每人10次射击成绩的平均数都为8.5环，方差分别为 $S_{甲}^{2} = 0.71$ ， $S_{乙}^{2} = 0.68$ ， $S_{丙}^{2} = 0.72$ ， $S_{丁}^{2} = 0.67$ ，则四人中成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 点（a，﹣1）在一次函数y＝﹣2x+1的图象上，则a的值为（　　）

A、a＝﹣3 B、a＝﹣1 C、a＝1 D、a＝2

查看试题解析
6. 如图，在平坦的地面上，为测量位于水塘旁的两点A ， B间的距离，先确定一点O ，分别取 $O A ， O B$ 的中点C ， D ，量得 $C D = 40$ m，则A ， B之间的距离是（）

A、20m B、40m C、60m D、80m

查看试题解析
7. 一次函数y＝3x-2的图象经过的象限是（）

A、第一、二、四象限 B、第一、二、三象限 C、第一、三、四象限 D、第二、三、四象限

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ A C B = 90 ° ， A C = 3 ， B C = 1$ ， $A C$ 在数轴上，点 $A$ 所表示的数为1，以点 $A$ 为圆心， $A B$ 长为半径画弧，在点 $A$ 左侧交数轴于点 $D$ ，则点 $D$ 表示的数是（）

A、 $\sqrt{10}$ B、 $- \sqrt{10}$ C、 $1 - \sqrt{10}$ D、 $\sqrt{10} - 1$

查看试题解析
9. 下面的性质中，平行四边形、矩形、菱形、正方形都具有的是（）

A、四边相等 B、对角线相等 C、对角线互相垂直 D、对角线互相平分

查看试题解析
10. 如图，以 $R t △ A B C$ 的三边为直角边分别向外作等腰直角三角形．若 $A B = \sqrt{5}$ ，则图中阴影部分的面积为（）

A、 $\frac{5}{2}$ B、 $10$ C、 $\frac{25}{2}$ D、 $5$

查看试题解析
11. 如图，在 $▱ A B C D$ 中，将 $△ A D C$ 沿 $A C$ 折叠后，点D恰好落在 $D C$ 的延长线上的点E处．若 $∠ B = 60 °$ ， $A B = 2$ ，则 $△ A D E$ 的周长为（）

A、6 B、9 C、12 D、15

查看试题解析
12. 如图，有一种动画程序，屏幕上正方形 $A B C D$ 是黑色区域（含正方形边界），其中 $A (1 ， 1)$ ， $B (2 ， 1)$ ， $C (2 ， 2)$ ， $D (1 ， 2)$ ，用信号枪沿直线 $y = - 2 x + b$ 发射信号，当信号遇到黑色区域时，区域便由黑变白，则能够使黑色区域变白的 $b$ 的取值范围为（）

A、 $3 \leq b \leq 6$ B、 $3 < b < 6$ C、 $- 3 \leq b \leq 0$ D、 $- 3 < b < 0$

查看试题解析

二、填空题

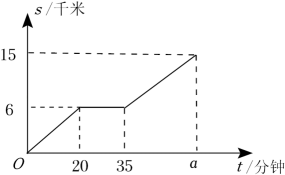
13. 若 $\sqrt{x - 1}$ 在实数范围内有意义，则实数x的取值范围是.

查看试题解析
14. 某校规定：学生的数学学期综合成绩是由平时、期中和期末三项成绩按3：3：4的比例计算所得．若某同学本学期数学的平时、期中和期末成绩分别是90分，90分和85分，则他本学期数学学期综合成绩是分．

查看试题解析
15. 周末时，达瓦在体育公园骑自行车锻炼身体，他匀速骑行了一段时间后停车休息，之后继续以原来的速度骑行．路程s（单位：千米）与时间t（单位：分钟）的关系如图所示，则图中的a＝．

查看试题解析
16. 如图，平行四边形 $A B C D$ 中， $A B ＝ 16 ， A D ＝ 12 ， ∠ A ＝ 60 °$ ， E是边 $A D$ 上一点，且 $A E ＝ 8 ， F$ 是边 $A B$ 上的一个动点，将线段 $E F$ 绕点E逆时针旋转 $60 °$ ，得到 $E G$ ，连接 $B G 、 C G$ ，则 $B G ＋ C G$ 的最小值是．

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{27} - \sqrt{8} + \sqrt{2} - \sqrt{12}$

(2)、 $\sqrt{3} \times \sqrt{18} \div \sqrt{6}$

查看试题解析
18. 如图，正方形网格的每个小方格边长均为1， $△ A B C$ 的顶点都在格点上．

(1)、 $A B =$ ， $B C =$ ， $A C =$ ；

(2)、判断 $△ A B C$ 的形状，并说明理由．

查看试题解析
19. 如图，在平行四边形ABCD中，E、F分别在AD、BC边上，且AE=CF．

求证：

(1)、△ABE≌△CDF；

(2)、四边形BFDE是平行四边形．

查看试题解析

20. 今年的4月15日是第七个全民国家安全教育日．今年的活动主题是“树牢总体国家安全观，感悟新时代国家安全成就，为迎接党的二十大胜利召开营造良好氛围”．某学校开展了国家安全知识竞赛．现从该校七、八年级中各随机抽取20名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分为整数，并用x表示），下面给出了部分信息：

七年级20名学生的竞赛成绩是：

95 80 85 100 85 95 90 65 85 75

90 90 70 90 100 80 80 90 95 75

八年级20名学生的竞赛成绩是：

80 80 60 95 65 100 90 80 85 85

95 75 80 90 70 80 95 75 100 90

【整理数据】

成绩x（分）	$60 \leq x \leq 70$	$70 < x \leq 80$	$80 < x \leq 90$	$90 < x \leq 100$
七年级	2	5	a	5
八年级	3	7	5	5

【分析数据】

统计量	平均数	中位数	众数
七年级	85.75	b	c
八年级	83.5	82.5	80

【应用数据】

(1)、直接写出：

a =

，

b =

，

c =

；

(2)、根据图表中的数据，判断七、八年级中哪个年级学生的竞赛成绩更好？请说明理由；

(3)、若七年级有1000人，八年级有800人参与竞赛，请估计七年级和八年级成绩大于80分的总人数．

查看试题解析

21. 如图，直线 $l_{1} ： y_{1} = - 3 x + 3$ 与 $x$ 轴交于点 $D$ ，与经过 $A (4 ， 0)$ 、 $B (3 ， - \frac{3}{2})$ 两点的直线 $l_{2} ： y_{2} = k x + b$ 交于点 $C$ ．

(1)、求直线 $l_{2}$ 的表达式；

(2)、求点 $C$ 的坐标；

(3)、根据图像直接写出：当 $y_{1} > y_{2}$ 时， $x$ 的取值范围．

查看试题解析
22. 台风是一种自然灾害，它以台风中心为圆心在周围上百千米范围内形成极端气候，有极强的破坏力．如图，有一台风中心沿东西方向 $A B$ 由 $A$ 向 $B$ 移动，已知点 $C$ 为海港， $A C = 300 k m$ ， $B C = 400 k m$ ， $∠ A C B = 90 °$ ，以台风中心为圆心周围 $260 k m$ 以内为受影响区域．

(1)、求海港 $C$ 到直线 $A B$ 的距离；

(2)、台风中心由 $A$ 向 $B$ 移动的过程中，海港 $C$ 受台风影响吗？为什么？

查看试题解析
23. 如图，在四边形 $A B C D$ 中， $A B ∥ C D$ ，过点D作 $∠ A D C$ 的角平分线交 $A B$ 于点E，连接 $A C$ 交 $D E$ 于点O， $A D ∥ C E$ ．

(1)、求证：四边形 $A E C D$ 是菱形；

(2)、若 $A D = 10$ ， $△ A C D$ 的周长为36，求菱形 $A E C D$ 的面积．

查看试题解析
24. 2022年世界杯期间，某商店购进A、B两种品牌的足球进行销售．销售5个A品牌和10个B品牌足球的利润和为700元，销售10个A品牌和5个B品牌足球的利润和为800元．

(1)、每个A品牌和B品牌足球的销售利润分别是多少元？

(2)、商店计划购进两种品牌足球共100个，设购进A品牌足球x个，两种品牌的足球全部销售完共获利y元．
①求y与x之间的函数关系式；
②若购进A品牌足球的个数不超过B品牌足球个数的4倍，应怎样进货销售利润最大，最大利润为多少？

查看试题解析
25.

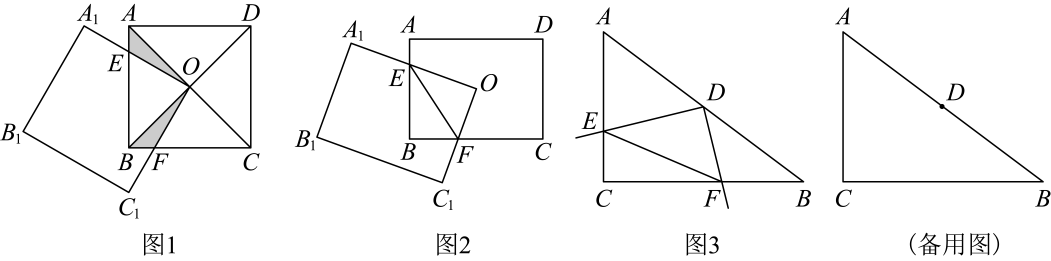(1)、【课本再现】如图1，正方形 $A B C D$ 的对角线相交于点 $O$ ，点 $O$ 又是正方形 $A_{1} B_{1} C_{1} O$ 的一个顶点，而且这两个正方形的边长都为1，四边形 $O E B F$ 为两个正方形重叠部分．正方形 $A_{1} B_{1} C_{1} O$ 可绕点 $O$ 转动．则下列结论正确的是（填序号即可）．

① $△ A E O ≌ △ B F O$ ；② $O E = O F$ ；③四边形 $O E B F$ 的面积总等于 $\frac{1}{4} S_{正方形 A B C D}$ ；④连接 $E F$ ，总有 $A E^{2} + C F^{2} = E F^{2}$ ．

(2)、【类比迁移】
如图2，矩形 $A B C D$ 的中心 $O$ 是矩形 $A_{1} B_{1} C_{1} O$ 的一个顶点， $A_{1} O$ 与边 $A B$ 相交于点 $E$ ， $C_{1} O$ 与边 $C B$ 相交于点 $F$ ，连接 $E F$ ，矩形 $A_{1} B_{1} C_{1} O$ 可绕着点 $O$ 旋转，猜想 $A E ， C F ， E F$ 之间的数量关系，并进行证明；

(3)、【拓展应用】
如图3，在 $R t △ A C B$ 中， $∠ C = 90 °$ ， $A C = 3 c m ， B C = 4 c m$ ，直角 $∠ E D F$ 的顶点 $D$ 在边 $A B$ 的中点处，它的两条边 $D E$ 和 $D F$ 分别与直线 $A C$ ， $B C$ 相交于点 $E ， F$ ， $∠ E D F$ 可绕着点 $D$ 旋转，当 $A E = 2 c m$ 时，求线段 $E F$ 的长度．

查看试题解析