(A卷)第三章 投影与三视图-浙教版数学九年级下册单元测试
试卷更新日期:2023-09-10 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列光线所形成的投影不是中心投影的是( )A、太阳光线 B、台灯的光线 C、手电筒的光线 D、路灯的光线3. 如图所示,该几何体从上面看所得到的平面图形是( )
2. 下列光线所形成的投影不是中心投影的是( )A、太阳光线 B、台灯的光线 C、手电筒的光线 D、路灯的光线3. 如图所示,该几何体从上面看所得到的平面图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 我国古代数学家利用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵、横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图所示的几何体是可以形成“牟合方盖”的一种模型,它从正面看是( )
4. 我国古代数学家利用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵、横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图所示的几何体是可以形成“牟合方盖”的一种模型,它从正面看是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图是由5个高度相等大小相同的圆柱搭成的几何体,从左边看是( )
5. 如图是由5个高度相等大小相同的圆柱搭成的几何体,从左边看是( )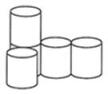 A、
A、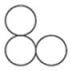 B、
B、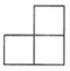 C、
C、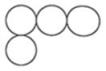 D、
D、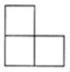 6. 如图是某个几何体的三视图,该几何体是( ).
6. 如图是某个几何体的三视图,该几何体是( ).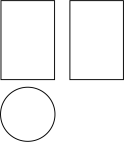 A、圆柱 B、圆锥 C、四棱柱 D、四棱锥7. 如图是某几何体的三视图,这个几何体可以是( )
A、圆柱 B、圆锥 C、四棱柱 D、四棱锥7. 如图是某几何体的三视图,这个几何体可以是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 一个正方体的平面展开图如图所示,将它折成正方体后,与汉字“冬”相对面上的汉字是( )
8. 一个正方体的平面展开图如图所示,将它折成正方体后,与汉字“冬”相对面上的汉字是( ) A、奥 B、林 C、匹 D、克9. 已知圆锥的底面半径为4,母线长为5,则圆锥的侧面积为( )A、 B、 C、 D、10. 如图,一圆柱体的底面周长为3πcm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,爬行的最短路程是( ).
A、奥 B、林 C、匹 D、克9. 已知圆锥的底面半径为4,母线长为5,则圆锥的侧面积为( )A、 B、 C、 D、10. 如图,一圆柱体的底面周长为3πcm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,爬行的最短路程是( ). A、3πcm B、5cm C、 cm D、 cm
A、3πcm B、5cm C、 cm D、 cm二、填空题(每空4分,共24分)
-
11. 已知同一时刻物体的高与影子的长成正比例.身高的小明的影子长为 , 这时测得一棵树的影长为 , 则这棵树的高为.12. 如图,物体在灯泡发出的光照射下形成的影子是投影.(填“平行”或“中心”).
 13. 写出一个几何体,使它的三视图都相同.(写出一个即可)14. 如图是由五个棱长均为1的正方体搭成的几何体,则它的左视图的面积为 .
13. 写出一个几何体,使它的三视图都相同.(写出一个即可)14. 如图是由五个棱长均为1的正方体搭成的几何体,则它的左视图的面积为 . 15. 小颖同学到学校领来n盒粉笔,整齐地摞在讲桌上,其三视图如图,则n的值是
15. 小颖同学到学校领来n盒粉笔,整齐地摞在讲桌上,其三视图如图,则n的值是 16. 圆柱的底面半径为 , 母线长为 , 则该圆柱的侧面积为.
16. 圆柱的底面半径为 , 母线长为 , 则该圆柱的侧面积为.三、解答题(共9题,共66分)
-
17. 如图,小明和小丽分别站在路灯OA的两侧点和点的位置,已知BD为小明在路灯下的影子,请你画出小丽在路灯下的影子CE.
 18. 如图,是由几个大小完全相同的小正方体垒成的几何体,请分别画出你所看到的几何体的三视图.
18. 如图,是由几个大小完全相同的小正方体垒成的几何体,请分别画出你所看到的几何体的三视图.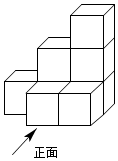 19. 下图是由一些大小相同的小正方体搭成的几何体的从上面看到的几何体的形状图,其中小正方形中的数字表示在该位置上的小立方体的个数,请你画出从正面、左面看到的几何体的形状图.
19. 下图是由一些大小相同的小正方体搭成的几何体的从上面看到的几何体的形状图,其中小正方形中的数字表示在该位置上的小立方体的个数,请你画出从正面、左面看到的几何体的形状图. 20. 如图,左面立体图形中四边形APQC表示平面截正方体的截面,请在右面展开图中画出四边形APQC的四条边.
20. 如图,左面立体图形中四边形APQC表示平面截正方体的截面,请在右面展开图中画出四边形APQC的四条边.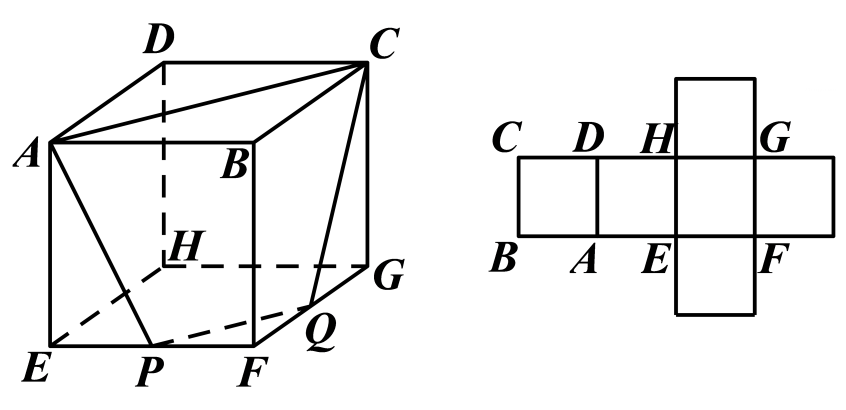 21. 在数学探究活动中,李明同学想利用影子测量旗杆的高度,他在某一时刻测得1m长的标杆影长为 , 同时当他测量教学楼前的旗杆的影长时,因旗杆靠近教学楼,有一部分影子在墙上,他测得旗杆到教学楼的距离 , 旗杆在教学楼墙上的影长 , 求旗杆的高.
21. 在数学探究活动中,李明同学想利用影子测量旗杆的高度,他在某一时刻测得1m长的标杆影长为 , 同时当他测量教学楼前的旗杆的影长时,因旗杆靠近教学楼,有一部分影子在墙上,他测得旗杆到教学楼的距离 , 旗杆在教学楼墙上的影长 , 求旗杆的高.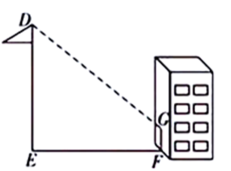 22. 如图是一个几何体的三视图,求该几何体的表面积.
22. 如图是一个几何体的三视图,求该几何体的表面积.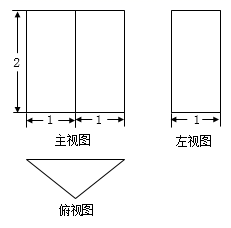 23. 如图是小明用10块棱长都为3cm的正方体搭成的几何体.
23. 如图是小明用10块棱长都为3cm的正方体搭成的几何体. (1)、分别画出从正面、从左面、从上面看到的所搭几何体的形状图;(2)、小明所搭几何体的表面积(包括与桌面接触的部分)是 .
(1)、分别画出从正面、从左面、从上面看到的所搭几何体的形状图;(2)、小明所搭几何体的表面积(包括与桌面接触的部分)是 .