（提升卷）3.4简单几何体的表面展开图-2023-2024年浙教版数学九年级下册同步测试

试卷更新日期：2023-09-10 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列各图形中，经过折叠能围成一个立方体的为（）

A、 B、 C、 D、

查看试题解析
2. 下面图形中，是直棱柱的表面展开图的是（）

A、 B、 C、 D、

查看试题解析
3. 如图所示，该正方体的展开图为（）

A、 B、 C、 D、

查看试题解析
4. 如图是每个面都标注了字母的立方体表面展开图.在展开前，与标注字母 $c$ 的面相对的面上的字母为（）

A、 $f$ B、 $e$ C、 $d$ D、 $a$

查看试题解析
5. 已知图1的小正方形和图2中所有的小正方形都全等，将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置，放置后所组成的图形是不能围成一个正方体的.那么安放的位置是（）

A、① B、② C、③ D、④

查看试题解析
6. 如图，从一块半径是 2 的圆形铁片上剪出一个圆心角为90°的扇形，将剪下来的扇形围成一个圆锥.那么这个圆锥的底面圆的半径是（）

A、 $\frac{π}{4}$ B、 $\frac{\sqrt{2}}{4}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{π}{2}$

查看试题解析
7. 如图，从一个边长是10的正五边形纸片上剪出一个扇形（阴影部分），将剪下来的扇形围成一个圆锥，这个圆锥的底面半径为（）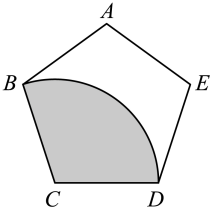

A、1 B、3 C、 $\frac{3}{2}$ D、2

查看试题解析
8. 已知圆锥底面半径为1，母线长为4，地面圆周上有一点A，一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B，则蚂蚁爬行的最短路程为（）

A、 $π$ B、 $\sqrt{5} π$ C、 $2 \sqrt{5}$ D、 $2 π$

查看试题解析
9. 如图，在四边形ABCD中，BC=CD=4，AB=7，AB⊥BC，CD⊥BC。把四边形ABCD绕AB旋转一周，则该几何体的表面积为（）

A、48π B、56π C、68π D、72π

查看试题解析
10.
如图1所示，一只封闭的圆柱形容器内盛了一半水（容器的厚度忽略不计），圆柱形容器底面直径为高的2倍，现将该容器竖起后如图2所示，设图1、图2中水所形成的几何体的表面积分别为S₁、S₂ ，则S₁与S₂的大小关系是（　　）

A、S₁≤S₂ B、S₁＜S₂ C、S₁＞S₂ D、S₁=S₂

查看试题解析

二、填空题（每空4分，共24分）

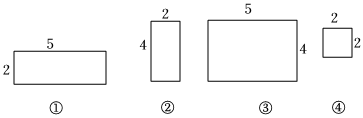
11. 仓库里有如图四种规格数量足够多的长方形、正方形的铁片 $($ 尺寸单位：分米 $)$ ；从中选5块铁片，焊接成一个无盖的长方体 $($ 或立方体 $)$ 铁盒 $($ 不浪费材料 $) .$ 甲型盒是由3种规格铁片焊接而成的表面积最大的铁盒，乙型盒是由2种规格铁片焊接而成的容积最小的铁盒.现在要分别做上述两种铁盒各100个，则至少需要 $②$ 号铁片块.

查看试题解析
12. 将一个容积为360cm³的包装盒剪开铺平，纸样如图所示．利用容积列出图中x（cm）满足的一元二次方程：（不必化简）．

查看试题解析
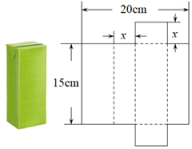13. 如图，硬纸片沿虛线折起来便可成一个正方体，与3号面相对的是号面。

查看试题解析
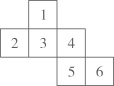14. 已知圆锥的底面半径和母线的长分别是一元二次方程 $x^{2} - 7 x + 12 = 0$ 的两个根，则圆锥的侧面积为．

查看试题解析
15. 已知一个直角三角形的两条直角边长分别为3和4，把它绕着其中一条直角边旋转一周，其余各边所成的面围成的几何体的表面积为.

查看试题解析
16. 已知 $R t Δ A B C$ ， $∠ C = 90 °$ ， $A B = 5 c m$ ， $A C = 4 c m$ ，将此三角形绕 $A C$ 旋转一周所形成的圆锥的侧面积是.

查看试题解析

三、解答题（共9题，共66分）

17. 在数学活动课中，同学们准备了一些等腰直角三角形纸片，从每张纸片中剪出一个扇形制作圆锥玩具模型.如图，已知△ABC是腰长为16cm的等腰直角三角形.

(1)、在等腰直角三角形ABC纸片中，以C为圆心，剪出一个面积最大的扇形(要求：尺规作图，保留作图痕迹，不写作法)；

(2)、请求出所制作圆锥底面的半径长.

查看试题解析
18. 有一个顶部是圆锥，底部是圆柱的粮囤模型，如图是它的主视图.

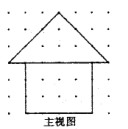(1)、画出该粮囤模型的俯视图；

(2)、若每相邻两个格点之间的距离均表示1米，请计算：
①在粮囤顶部铺上油毡，需要多少平方米油毡（油毡接缝重合部分不计）？

②若粮食最多只能装至与圆柱同样高，则最多可以存放多少立方米粮食？（结果保留 $π$ 和根号）

查看试题解析
19. 如图，已知圆柱底面的直径 $B C = 8$ ，圆柱的高 $A B = 10$ ，在圆柱的侧面上，过点 $A$ ， $C$ 嵌有一圈长度最短的金属丝.

(1)、现将圆柱侧面沿 $A B$ 剪开，所得的圆柱侧面展开图是______.

A、； B、； C、； D、

(2)、求该长度最短的金属丝的长.

查看试题解析
20. 如图，在正方形网格图中建立平面直角坐标系，一条圆弧经过格点A（0，4）、B（-4，4）、C（-6，2），若该圆弧所在圆的圆心为D点，请你利用网格图回答下列问题：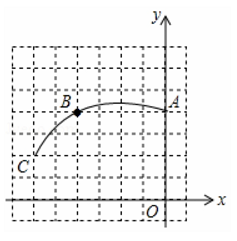

(1)、圆心D的坐标为；

(2)、若扇形ADC是一个圆锥的侧面展开图，求该圆锥底面圆的半径长（结果保留根号）.

查看试题解析
21. 如图，在边长为120cm的正方形铁皮ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体工艺盒（A，B，C，D四个顶点正好重合于上底面一点）.已知点M，N在CD边上，且是被剪去的一个等腰直角三角形斜边的两个端点，设CM＝DN＝x（cm）.

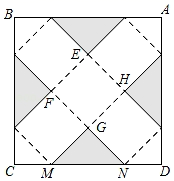(1)、若折成的包装盒恰好是个正方体，求这个工艺盒的体积；

(2)、当x取何值时，工艺盒的四个侧面面积和S最大，最大值为多少？

查看试题解析
22. 如图1，小明用一张边长为6 dm的正三角形硬纸板设计一个无盖的正三棱柱糖果盒，从三个角处分别剪去一个形状大小相同的四边形，其一边长记为x dm，再折成如图2所示的无盖糖果盒，它的容积记为y dm³.

(1)、y关于x的函数关系式是，自变量x的取值范围是.

(2)、为探究y随x的变化规律，小明类比二次函数进行了如下探究：
①列表：请你补充表格中的数据；

x

0

0.5

1

1.5

2

2.5

3

y

0

3.125

3.375

0.625

0

②描点：请你把上表中各组对应值作为点的坐标，在平面直角坐标系中描出相应的点；

③连线：请你用光滑的曲线顺次连接各点.

(3)、利用函数图象解决：
①该糖果盒的最大容积是；

②若该糖果盒的容积超过2 dm³ ，请估计糖果盒的底边长a的取值范围.（保留一位小数）

查看试题解析
23. 将立方体纸盒沿某些棱剪开，且使六个面连在一起，然后铺平，可以得到其表面展开图的平面图形.

(1)、以下两个方格图中的阴影部分能表示立方体表面展开图的是（填A或B）.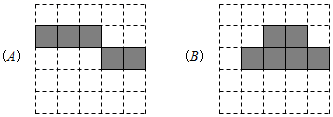

(2)、在以下方格图中，画一个与（1）中呈现的阴影部分不相似（包括不全等）的立方体表面展开图.（用阴影表示）

(3)、如图中的实线是立方体纸盒的剪裁线，请将其表面展开图画在右图的方格图中.（用阴影表示）

查看试题解析

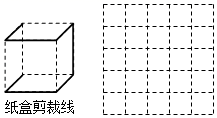
24. 根据以下素材，探索完成任务。

圆柱体外包装的材料损耗率问题研究
素材1	厂商在生产产品时，对产品外包装的材料，通常要考虑尽可能地合理利用，减少浪费。圆柱体形状的物品，它的外包装盒通常都是长方体，且上下底面为正方形。
素材2	设计产品外包装时，我们把裁剪掉的废料部分的面积与原图形的面积之比称为材料的损耗率。一种材料利用率较高的裁剪方式如图所示，采用正方形纸板裁剪，只需剪掉四条边上的四个小三角形。按这种方式包装一个底面直径为2，高为1的圆柱体(接缝处的材料损耗不计)，损耗率只有 $\frac{2}{18}$ ≈11.1%．
	问题解决
任务1	现采用一张边长为4 $\sqrt{2}$ cm的正方形纸，按如图所示的裁剪方式剪掉各边上的四个三角形后，可恰好无缝地做成一个圆柱体的外包装盒，设圆柱体的底面半径为r，则它的高h= ▲ (用r的代数式表示)
任务2	在上图中，若已知该圆柱体外包装盒的材料损耗率为16%，求这个圆柱体的底面半径r
任务3	现利用两块同样大小的正方形纸板，按如图方式裁剪后，可包装两个高分别为4和2的圆柱体，发现这两个圆柱体的体积恰好相等．求第一个圆柱体的底面半径．(圆柱体的体积=底面积×高)

查看试题解析

25. 图1、图2为同一长方体房间的示意图，图3为该长方体的表面展开图．

(1)、蜘蛛在顶点A′处．
①苍蝇在顶点B处时，试在图1中画出蜘蛛为捉住苍蝇，沿墙面爬行的最近路线．
②苍蝇在顶点C处时，图2中画出了蜘蛛捉住苍蝇的两条路线，往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC，试通过计算判断哪条路线更近．

(2)、在图3中，半径为10dm的⊙M与D′C′相切，圆心M到边CC′的距离为15dm，蜘蛛P在线段AB上，苍蝇Q在⊙M的圆周上，线段PQ为蜘蛛爬行路线，若PQ与⊙M相切，试求PQ长度的范围．

查看试题解析

x	0	0.5	1	1.5	2	2.5	3
y	0	3.125		3.375		0.625	0