(培优卷)3.4简单几何体的表面展开图-2023-2024年浙教版数学九年级下册同步测试
试卷更新日期:2023-09-10 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,折成正方体后,如果相对面所对应的值相等,那么x的平方与y的立方根之和为( )
 A、2 B、3 C、4 D、52. 如图,一个正方体骰子的六个面上分别标有1至6共六个数字,且相对面数字之和相同,将骰子按如图所示方式放置并按箭头方向无滑动翻转后停止在M处,则停止后骰子朝上面的数字为( )
A、2 B、3 C、4 D、52. 如图,一个正方体骰子的六个面上分别标有1至6共六个数字,且相对面数字之和相同,将骰子按如图所示方式放置并按箭头方向无滑动翻转后停止在M处,则停止后骰子朝上面的数字为( ) A、3 B、4 C、5 D、63. 如图,在矩形中,以点A为圆心,以长为半径画弧交于点E,将扇形剪下来做成圆锥,若 , 则该圆锥底面半径为( )
A、3 B、4 C、5 D、63. 如图,在矩形中,以点A为圆心,以长为半径画弧交于点E,将扇形剪下来做成圆锥,若 , 则该圆锥底面半径为( )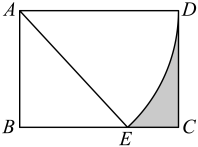 A、 B、 C、3 D、4. 有一个装有某种液体的圆柱体容器,底面半径为4cm,高为12cm.小强不小心碰倒容器,当容器水平静置时其截面如图所示,其中圆心O到液面AB的距离为2cm,若将该容器扶正竖直放置,则容器内液体的高度为( )
A、 B、 C、3 D、4. 有一个装有某种液体的圆柱体容器,底面半径为4cm,高为12cm.小强不小心碰倒容器,当容器水平静置时其截面如图所示,其中圆心O到液面AB的距离为2cm,若将该容器扶正竖直放置,则容器内液体的高度为( ) A、 B、 C、 D、5. 有一个不完整圆柱形玻璃密封容器如图①,测得其底面半径为a , 高为h , 其内装蓝色液体若干.若如图②放置时,测得液面高为 ;若如图③放置时,测得液面高为 则该玻璃密封容器的容积 圆柱体容积 底面积 高 是 . (结果保留 )
A、 B、 C、 D、5. 有一个不完整圆柱形玻璃密封容器如图①,测得其底面半径为a , 高为h , 其内装蓝色液体若干.若如图②放置时,测得液面高为 ;若如图③放置时,测得液面高为 则该玻璃密封容器的容积 圆柱体容积 底面积 高 是 . (结果保留 ) 6. 在正方体的表面上画有如图1中所示的粗线,图2是其展开图的示意图,但只在A面上画有粗线,那么将图1中剩余两个面中的粗线画入图2中,画法正确的是( )
6. 在正方体的表面上画有如图1中所示的粗线,图2是其展开图的示意图,但只在A面上画有粗线,那么将图1中剩余两个面中的粗线画入图2中,画法正确的是( )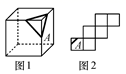 A、
A、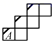 B、
B、 C、
C、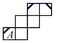 D、
D、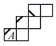 7. 有一种正方体如图所示,下列图形是该方体的展开图的是( )
7. 有一种正方体如图所示,下列图形是该方体的展开图的是( )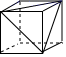 A、
A、 B、
B、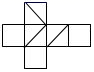 C、
C、 D、
D、 8. 如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出5cm,宽留出1cm,则该六棱柱的侧面积是( )
8. 如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出5cm,宽留出1cm,则该六棱柱的侧面积是( )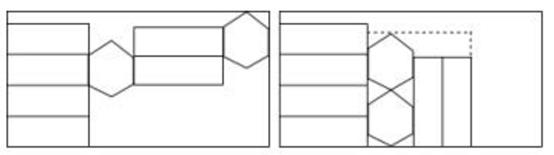 A、(108- )cm2 B、(108- )cm2 C、(54- )cm2 D、(54- )cm29. 如图,线段AB和CD是正方体表面两正方形的对角线,将此正方体沿部分棱剪开,展成一个平面图形后,AB和CD可能出现下列关系中的哪几种? 、B、C、D四点在同一直线上 正确的结论是( )
A、(108- )cm2 B、(108- )cm2 C、(54- )cm2 D、(54- )cm29. 如图,线段AB和CD是正方体表面两正方形的对角线,将此正方体沿部分棱剪开,展成一个平面图形后,AB和CD可能出现下列关系中的哪几种? 、B、C、D四点在同一直线上 正确的结论是( )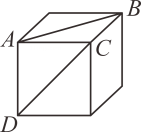 A、 B、 C、 D、10. 正如我们小学学过的圆锥体积公式V= πr2h(π表示圆周率,r表示圆锥的底面半径,h表示圆锥的高)一样,许多几何量的计算都要用到π.祖冲之是世界上第一个把π计算到小数点后7位的中国古代科学家,创造了当时世界上的最高水平,差不多过了1000年,才有人把π计算得更精确.在辉煌成就的背后,我们来看看祖冲之付出了多少.现在的研究表明,仅仅就计算来讲,他至少要对9位数字反复进行130次以上的各种运算,包括开方在内.即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力,值得我们学习.
A、 B、 C、 D、10. 正如我们小学学过的圆锥体积公式V= πr2h(π表示圆周率,r表示圆锥的底面半径,h表示圆锥的高)一样,许多几何量的计算都要用到π.祖冲之是世界上第一个把π计算到小数点后7位的中国古代科学家,创造了当时世界上的最高水平,差不多过了1000年,才有人把π计算得更精确.在辉煌成就的背后,我们来看看祖冲之付出了多少.现在的研究表明,仅仅就计算来讲,他至少要对9位数字反复进行130次以上的各种运算,包括开方在内.即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力,值得我们学习.下面我们就来通过计算解决问题:已知圆锥的侧面展开图是个半圆,若该圆锥的体积等于9 π,则这个圆锥的高等于( )
A、 B、 C、 D、二、填空题(每空4分,共20分)
-
11. 在一个长为5 米, 宽为3米的长方形草地 上, 如图堆放着一根正三棱柱的木块,它的侧棱长平行且大于场地宽 , 木块的主视图是边长为1 米的正三角形, 一只蚂蚁从 点处到处需要走的最短路程是米.
 12. 如图1是三个直立于水面上的形状完全相同的几何体(下底面为圆面,单位:厘米),将它们拼成如图2的新几何体,求该新几何体的体积(结果保留);
12. 如图1是三个直立于水面上的形状完全相同的几何体(下底面为圆面,单位:厘米),将它们拼成如图2的新几何体,求该新几何体的体积(结果保留); 13. 一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为cm3.14. 如图,长方体的棱AB长为4,棱BC长为3,棱BF长为2,P为HG的中点,一只蚂蚁从点A出发,沿长方体的表面爬行到点 处吃食物,那么它爬行的最短路程是.
13. 一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为cm3.14. 如图,长方体的棱AB长为4,棱BC长为3,棱BF长为2,P为HG的中点,一只蚂蚁从点A出发,沿长方体的表面爬行到点 处吃食物,那么它爬行的最短路程是. 15. 如图,圆锥的母线长OA为8,底面圆的半径为4.若一只蚂蚁在底面上点A处,在相对母线OC的中点B处有一只小虫,蚂蚁要捉小虫,需要爬行的最短路程为.
15. 如图,圆锥的母线长OA为8,底面圆的半径为4.若一只蚂蚁在底面上点A处,在相对母线OC的中点B处有一只小虫,蚂蚁要捉小虫,需要爬行的最短路程为.
三、解答题(共9题,共70分)
-
16. 图(1)是一个棱长为2的正方体空盒子ABCD﹣EFGH.图(2)是取AB,BC,BF边上的中点M,N,P,截去一个角后剩下的几何体.图(3)的8×8的网格中每一小格的边长都是1,请在这个网格中画出它的一种展开图.(要求所有的顶点都在格点上,且AM,CN,PF这三条棱中最多只能剪开一条棱)
 17. 在平面直角坐标系中,△ABC的位置如图所示(每个小正方形的边长为1).
17. 在平面直角坐标系中,△ABC的位置如图所示(每个小正方形的边长为1). (1)、△ABC与△A1B1C1是以点P为位似中心的位似图形,且他们的顶点均在格点上,则点P的坐标为;(2)、将△ABC绕点A逆时针方向旋转135°,
(1)、△ABC与△A1B1C1是以点P为位似中心的位似图形,且他们的顶点均在格点上,则点P的坐标为;(2)、将△ABC绕点A逆时针方向旋转135°,①画出旋转后的△AB2C2;
②用线段AB旋转到线段AB2 , 所扫过的图形面积做一个圆锥的侧面(接缝忽略不计),求这个圆锥的底面圆半径.(保留精确值)
18. 如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.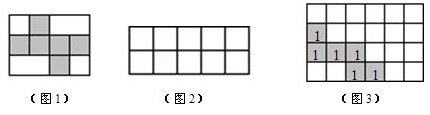 (1)、计算图1长方形的面积;(2)、小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);(3)、如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.19. 综合实践
(1)、计算图1长方形的面积;(2)、小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);(3)、如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.19. 综合实践问题情景:某综合实践小组进行废物再利用的环保小卫士行动. 他们准备用废弃的宣传单制作装垃圾的无盖纸盒.
操作探究:
(1)、若准备制作一个无盖的正方体形纸盒,如图1,下面的哪个图形经过折叠能围成无盖正方体形纸盒?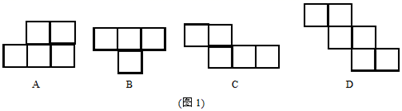 (2)、如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的是哪个字?
(2)、如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的是哪个字?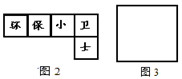 (3)、如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体形纸盒.
(3)、如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体形纸盒.①请你在图3中画出示意图,用实线表示剪切线,虚线表示折痕.
②若四角各剪去了一个边长为xcm的小正方形,用含x的代数式表示这个纸盒的高以及底面积,当小正方形边长为4cm时,求纸盒的容积.
20. 综合与实践问题情境:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l,圆心角为的扇形.工人在制作圆锥形物品时,通常要先确定扇形圆心角度数,再度量裁剪材料.
 (1)、探索尝试:图1中,圆锥底面周长与其侧面展开图的弧长;(填“相等”或“不相等”)若 , , 则n=.(2)、解决问题:为操作简便,工人希望能简洁求n的值,请用含r,l的式子表示n;(3)、拓展延伸:图2是一种纸质圆锥形生日帽, , , C是中点,现要从点A到点C再到点A之间拉一装饰彩带,求彩带长度的最小值.21. 【问题情境】
(1)、探索尝试:图1中,圆锥底面周长与其侧面展开图的弧长;(填“相等”或“不相等”)若 , , 则n=.(2)、解决问题:为操作简便,工人希望能简洁求n的值,请用含r,l的式子表示n;(3)、拓展延伸:图2是一种纸质圆锥形生日帽, , , C是中点,现要从点A到点C再到点A之间拉一装饰彩带,求彩带长度的最小值.21. 【问题情境】小圣所在的综合实践小组准备制作一些无盖纸盒收纳班级讲台上的粉笔.

【操作探究】
(1)、图1中的哪些图形经过折叠能围成无盖正方体纸盒?(填序号).(2)、小圣所在的综合实践小组把折叠成6个棱长都为的无盖正方体纸盒摆成如图2所示的几何体.①请计算出这个几何体的体积;
②如果在这个几何体上再添加一些相同的正方体纸盒,并保持从上面看到的形状和从左面看到的形状不变,最多可以再添加 个正方体纸盒.
22. 如图1是边长为 的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计). (1)、设剪去的小正方形的边长为 ,折成的长方体盒子的容积为 ,直接写出用只含字母 的式子表示这个盒子的高为 ,底面积为 ,盒子的容积 为 ,(2)、为探究盒子的体积与剪去的小正方形的边长 之间的关系,小明列表分析:
(1)、设剪去的小正方形的边长为 ,折成的长方体盒子的容积为 ,直接写出用只含字母 的式子表示这个盒子的高为 ,底面积为 ,盒子的容积 为 ,(2)、为探究盒子的体积与剪去的小正方形的边长 之间的关系,小明列表分析:1
2
3
4
5
6
7
8
324
588
576
500
252
128
填空:① , ;
②由表格中的数据观察可知当 的值逐渐增大时, 的值.(从“逐渐增大”,“逐渐减小”“先增大后减小”,“先减小后增大”中选一个进行填空)
23. 如图所示,D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连结AB,AC,AD,E为AD上一点,连结BE,CE.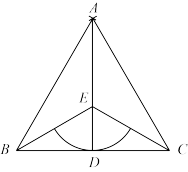 (1)、求证:BE = CE.(2)、以点E为圆心作与BC相切,分别交BE,CE于点F,G.若BC = 4,∠EBD = 30°,求扇形FEG的面积(3)、若用扇形FEG围成一个圆锥的侧面,求这个圆锥的底面圆的半径.24. 用如图所示的甲、乙、丙木板做一个长、宽、高分别为a厘米,b厘米,h厘米的长方体有盖木箱(a>b),其中甲刚好能做成箱底和一个长侧面,乙刚好能做成一个长侧面和一个短侧面,丙刚好能做成箱盖和一个短侧面。
(1)、求证:BE = CE.(2)、以点E为圆心作与BC相切,分别交BE,CE于点F,G.若BC = 4,∠EBD = 30°,求扇形FEG的面积(3)、若用扇形FEG围成一个圆锥的侧面,求这个圆锥的底面圆的半径.24. 用如图所示的甲、乙、丙木板做一个长、宽、高分别为a厘米,b厘米,h厘米的长方体有盖木箱(a>b),其中甲刚好能做成箱底和一个长侧面,乙刚好能做成一个长侧面和一个短侧面,丙刚好能做成箱盖和一个短侧面。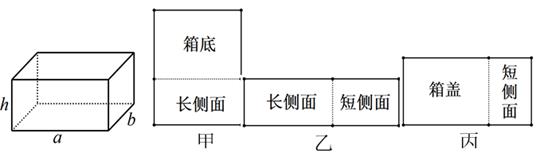 (1)、填空:用含a、b、h的代数式表示以下面积:
(1)、填空:用含a、b、h的代数式表示以下面积:甲的面积;乙的面积;丙的面积.
(2)、当h=20cm时,若甲的面积比丙的面积大200cm2 , 乙的面积为1400cm2 , 求a和b的值;(3)、现将一张长、宽分别为a厘米、b厘米的长方形纸板(如图①)分割成两个小长方形。左侧部分刚好分割成两个最大的等圆,和右侧剩下部分刚好做成一个圆柱体模型(如图②),且这样的圆柱体模型的高刚好与木箱的高相等。问:一个上述长方体木箱中最多可以放个这样的圆柱体模型。