(基础卷)3.4简单几何体的表面展开图-2023-2024年浙教版数学九年级下册同步测试
试卷更新日期:2023-09-10 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如下图,不是正方体展开图的是( )A、
 B、
B、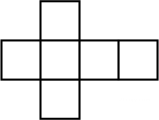 C、
C、 D、
D、 2. “争创全国文明典范城市,让文明成为宜昌人民的内在气质和城市的亮丽名片”.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是( ).
2. “争创全国文明典范城市,让文明成为宜昌人民的内在气质和城市的亮丽名片”.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是( ). A、文 B、明 C、典 D、范3. 下列图形中是棱锥的侧面展开图的是( )A、
A、文 B、明 C、典 D、范3. 下列图形中是棱锥的侧面展开图的是( )A、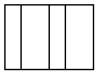 B、
B、 C、
C、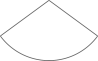 D、
D、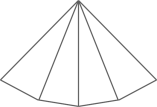 4. 如图,将一个无盖正方体盒子展开成平面图形的过程中,需要剪开的棱的条数是( )
4. 如图,将一个无盖正方体盒子展开成平面图形的过程中,需要剪开的棱的条数是( ) A、2条 B、3条 C、4条 D、5条5. 如果圆锥侧面展开图的面积是 , 母线长是 , 则这个圆锥的底面半径是( )A、3 B、4 C、5 D、66. 如图,冰淇淋蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积(接缝忽略不计)是( )
A、2条 B、3条 C、4条 D、5条5. 如果圆锥侧面展开图的面积是 , 母线长是 , 则这个圆锥的底面半径是( )A、3 B、4 C、5 D、66. 如图,冰淇淋蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积(接缝忽略不计)是( )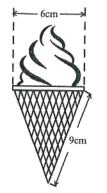 A、 B、 C、 D、7. 如图,在纸上剪一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径 , 扇形的圆心角等于 , 则围成的圆锥的母线长R的值为( )
A、 B、 C、 D、7. 如图,在纸上剪一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径 , 扇形的圆心角等于 , 则围成的圆锥的母线长R的值为( )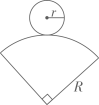 A、2 B、4 C、8 D、108. 张芳家有一个圆柱形的塑料桶,体积是 , 底面半径为x,则这个塑料桶的高为( )A、 B、 C、 D、9. 已知矩形两边长为2cm与3cm,绕长边旋转一周所得几何体的体积为( )A、3πcm3 B、4πcm3 C、12πcm3 D、18πcm310. 已知圆柱体的底面半径为 ,高为 ,则圆柱体的侧面积为( ).A、 B、 C、 D、
A、2 B、4 C、8 D、108. 张芳家有一个圆柱形的塑料桶,体积是 , 底面半径为x,则这个塑料桶的高为( )A、 B、 C、 D、9. 已知矩形两边长为2cm与3cm,绕长边旋转一周所得几何体的体积为( )A、3πcm3 B、4πcm3 C、12πcm3 D、18πcm310. 已知圆柱体的底面半径为 ,高为 ,则圆柱体的侧面积为( ).A、 B、 C、 D、二、填空题(每空4分,共24分)
-
11. 如图,是一个正方体的展开图,那么写有“青”字面的对面上的字是 .
 12. 某种无盖的长方体包装盒的展开图如图所示.根据图中数据计算,这种药品包装盒的体积是.
12. 某种无盖的长方体包装盒的展开图如图所示.根据图中数据计算,这种药品包装盒的体积是. 13. 若圆锥的底面半径是2,侧面展开图是一个圆心角为120的扇形,则该圆锥的母线长是 .14. 已知圆锥的底面半径是3cm,母线长为6cm,侧面积为 .15. 已知圆柱的底面半径是 , 圆柱的体积随着高的变化而变化,那么与之间的关系式为.16. 如图是某圆柱体果罐,它的主视图是边长为 的正方形,该果罐侧面积为 .
13. 若圆锥的底面半径是2,侧面展开图是一个圆心角为120的扇形,则该圆锥的母线长是 .14. 已知圆锥的底面半径是3cm,母线长为6cm,侧面积为 .15. 已知圆柱的底面半径是 , 圆柱的体积随着高的变化而变化,那么与之间的关系式为.16. 如图是某圆柱体果罐,它的主视图是边长为 的正方形,该果罐侧面积为 .
三、解答题(共8题,共66分)
-
17. 如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
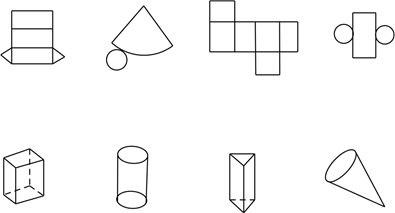 18. 如图,将弧长为 ,圆心角为120°的扇形纸片 围成圆锥形纸帽,使扇形的两条半径 与 重合(接缝粘连部分忽略不计),求圆锥的底面圆半径及圆锥的侧面积.
18. 如图,将弧长为 ,圆心角为120°的扇形纸片 围成圆锥形纸帽,使扇形的两条半径 与 重合(接缝粘连部分忽略不计),求圆锥的底面圆半径及圆锥的侧面积. 19. 将一根底面半径是5厘米的圆柱体木料锯成三段(每段都是圆柱体),其表面积增加了多少平方厘米?(取3.14)20. 将一个底面直径是20厘米,高为9厘米的“矮胖”形圆柱,锻压成底面直径是10厘米的“痩长”形圆柱,高变成了多少?
19. 将一根底面半径是5厘米的圆柱体木料锯成三段(每段都是圆柱体),其表面积增加了多少平方厘米?(取3.14)20. 将一个底面直径是20厘米,高为9厘米的“矮胖”形圆柱,锻压成底面直径是10厘米的“痩长”形圆柱,高变成了多少? 21. 如图,由5个相连的正方形可以折成一个无盖的正方体盒子.请你再画出3种不同的由5个正方形相连组成的图形,使它可以折成一个无盖的正方体盒子.
21. 如图,由5个相连的正方形可以折成一个无盖的正方体盒子.请你再画出3种不同的由5个正方形相连组成的图形,使它可以折成一个无盖的正方体盒子.