（提升卷）3.1投影-2023-2024年浙教版数学九年级下册同步测试

试卷更新日期：2023-09-10 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 太阳发出的光照在物体上是，路灯发出的光照在物体上是（）

A、平行投影，中心投影 B、中心投影，平行投影 C、平行投影，平行投影 D、中心投影，中心投影

查看试题解析
2. 一个矩形木框在太阳光的照射下，在地面上的投影不可能是（）

A、 B、 C、 D、

查看试题解析
3. 如图，正方形纸板的一条对角线重直于地面，纸板上方的灯（看作一个点）与这条对角线所确定的平面垂直于纸板，在灯光照射下，正方形纸板在地面上形成的影子的形状可以是（）

A、 B、 C、 D、

查看试题解析
4. 如图是一根电线杆在一天中不同时刻的影长图，试按其 $-$ 天中发生的先后顺序排列，正确的是（）

A、①②③④ B、④①③② C、④②③① D、④③②①

查看试题解析
5. 如图，AB表示一个窗户的高，AM和BN表示射入室内的光线，窗户的下端到地面距离BC＝1米，已知某一时刻BC在地面的影长CN＝1.5米，AC在地面的影长CM＝4.5米，则AB高为（）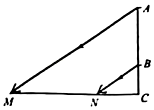

A、3.5 B、2 C、1.5 D、2.5

查看试题解析
6. 如图，为测量楼高 $A B$ ，在适当位置竖立一根高 $2 m$ 的标杆 $M N$ ，并在同一时刻分别测得其落在地面上的影长 $A C = 20 m ， M P = 2.5 m$ ，则楼高 $A B$ 为（）

A、 $15 m$ B、 $16 m$ C、 $18 m$ D、 $20 m$

查看试题解析
7. 大约在两千四五百年前，墨子和他的学生做了世界上第1个小孔成倒像的实验．并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图所示的小孔成像实验中，若物距为 $10 c m$ ，像距为 $15 c m$ ，蜡烛火焰倒立的像的高度是 $8 c m$ ，则蜡烛火焰的高度是（）

A、 $\frac{9}{2}$ B、6 C、 $\frac{16}{3}$ D、8

查看试题解析
8. 如图，在直角坐标系中，点P(2，2)是一个光源．木杆AB两端的坐标分别为(0，1)，(3，1)．则木杆AB在x轴上的投影长为（）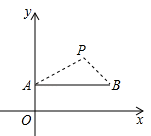

A、3 B、4 C、5 D、6

查看试题解析
9. 如图，小明居住的小区内有一条笔直的小路，有一盏路灯位于小路上 $M 、 N$ 两点的正中间，晚上，小明由点 $M$ 处径直走到点 $N$ 处，他在灯光照射下的影长 $y$ 与行走路程 $x$ 之间的变化关系用图象表示大致是（）

A、 B、 C、 D、

查看试题解析
10. 如图，某剧院舞台上的照明灯P射出的光线成“锥体”，其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6 m的正方形，要使灯光能照射到整个舞台，则灯P的悬挂高度是（）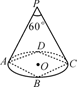

A、 m B、 3 m C、 3 m D、 4 m

查看试题解析

二、填空题（每空4分，共24分）

11. 在阳光下，一名同学测得一根长为1米的竹竿的影长为0.8米．同时另一名同学测量一棵树的高度时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上，其影长为0.6米，落在地面上的影长为3.6米，则树高为米．

查看试题解析
12. 如图，小树AB在路灯O的照射下形成树影BC．若树高AB=2m，树影BC=3m，树与路灯的水平距离BP=5m，则路灯的高度OP为 m．

查看试题解析
13. 如图，电线杆上的路灯距离地面 $8 m$ ，身高 $1.6 m$ 的小明（ $A B$ ）站在距离电线杆的底部（点O） $20 m$ 的A处，则小明的影子 $A M$ 长为m.

查看试题解析
14. 如图，在平面直角坐标系中，△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形，点B、B′的坐标分别为（3，1）、（6，2）若点A的坐标为（ $\frac{5}{2}$ ，3），则点A′的坐标为．

查看试题解析
15. 《孙子算经》是中国古代重要的数学著作，其中有首歌谣：“今有竿不知其长，量得影长一百五十寸，立一标杆，长一十五寸，影长五寸，问竿长几何？”．其意思是：“如图，有一根竹竿 $A B$ 不知道有多长，量出它在太阳下的影子 $B C$ 长150寸，同时立一根15寸的小标杆 $D E$ ，它的影子 $E F$ 长5寸，则竹竿 $A B$ 的长为多少？”．答：竹竿 $A B$ 的长为寸．

查看试题解析
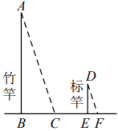16. 公元前6世纪，古希腊学者泰勒斯用图1的方法巧测金字塔的高度.如图2，小明仿照这个方法，测量圆锥形小山包的高度，已知圆锥底面周长为62.8 m. 先在小山包旁边立起一根木棒，当木棒影子长度等于木棒高度时，测得小山包影子AB长为23 m（直线AB过底面圆心），则小山包的高为m（π取3.14）.

查看试题解析

三、解答题（共8题，共66分）

17. 如图

(1)、如图①，在8×6的网格图中，每个小正方形边长均为1，原点O和△ABC的顶点均为格点．点C坐标为（2，4），以O为位似中心，在网格图中作△A′B'C′，使△A′B'C′与△ABC位似，且位似比为1∶2，（保留作图痕迹），则点C'的坐标为，周长比C_△A_'B_'C_′∶C_△ABC＝．

(2)、如图②，AB和DE是直立在地面上的两根立柱．AB＝6m，某一时刻AB在阳光下的投影BC＝4m，DE在阳光下的投影长为6cm．请你在图中②画出此时DE在阳光下的投影EF．根据题中信息，求得立柱DE的长为 ▲ m．

查看试题解析
18. 某小组的项目式学习活动内容是测量某棵古树的高度 $A B$ ，如图，在阳光下，某一时刻，古树 $A B$ 的影子落在了地上和围墙上，落在地上的长度 $B D = 21$ 米，落在墙上的长度 $D E = 1$ 米，在古树的附近有一棵小树 $M N$ ，同一时刻，小树的影长 $P N = 1.8$ 米，小树的高 $M N = 1.2$ 米．已知点N，P，B，D在一条水平线上， $M N ⊥ N D$ ， $A B ⊥ N D$ ， $E D ⊥ N D$ ，请求出该古树的高度 $A B$ ．

查看试题解析
19. 如图，河对岸有一路灯杆 $A B$ ，在灯光下，小明在点D处，自己的影长 $D F = 4 m$ ，沿 $B D$ 方向到达点F处再测自己的影长 $F G = 5 m$ ，如果小明的身高为 $1.6 m$ ，求路灯杆 $A B$ 的高度.

查看试题解析
20. 如图，一路灯 $A B$ 与墙 $O P$ 相距20米，当身高 $C D = 1.6$ 米的小亮在离墙17米的D处时，影长 $D G$ 为1米．

(1)、求路灯B的高度；

(2)、若点P为路灯，请画出小亮位于N处时，在路灯P下的影子NF（用粗线段表示出来）

查看试题解析
21. 如图，某墙壁左侧有一木杆 $D P$ 和一棵松树 $A B$ .某一时刻在太阳光下，木杆 $D P$ 的影子刚好不落在墙壁上，已知 $A B ⊥ B P$ ， $D P ⊥ B P$ .

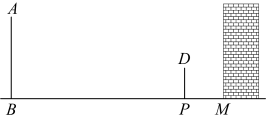(1)、请画出在同一时刻下松树AB在阳光下的投影 $B C$ ；

(2)、若木杆 $D P = 2 m$ ，木杆DP的投影 $P M = 2.5 m$ ，同一时刻松树AB在阳光下的投影 $B C = 10 m$ ，求松树 $A B$ 的高度.

查看试题解析
22. 某校数学社团开展“探索生活中的数学”研学活动，准备测量秦始皇雕塑 $A B$ 的高度.如图所示，首先，在阳光下，某一时刻，小玉在雕塑影子顶端 $D$ 处竖立一根高2米的标杆 $C D$ ，此时测得标杆 $C D$ 的影子 $D E$ 为2米；然后，在 $H$ 处竖立一根高2.5米的标杆 $G H$ ，小婷从 $H$ 处沿 $B H$ 后退0.8米到 $N$ 处恰好看到点 $G$ 、 $A$ 在一条直线上，小婷的眼睛到地面的距离 $M N = 1.5$ 米， $D N = 24$ 米，已知 $C D ⊥ E N$ ， $A B ⊥ E N$ ， $G H ⊥ E N$ ， $M N ⊥ E N$ ，点 $E$ 、 $D$ 、 $B$ 、 $H$ 、 $N$ 在同一水平直线上，请根据以上数据求出秦始皇雕塑 $A B$ 的高度.

查看试题解析
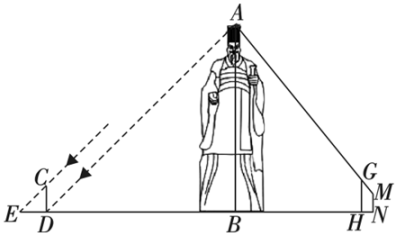23. 如图，一根灯杆 $A B$ 上有一盏路灯A，路灯A离水平地面的高度为9米，在距离路灯正下方B点15.5米处有一坡度为 $i = 1 ： \frac{4}{3}$ 的斜坡 $C D$ ，如果高为3米的标尺 $E F$ 竖立地面 $B C$ 上，垂足为F，它的影子的长度为4米．

(1)、当影子全在水平地面 $B C$ 上（图1），求标尺与路灯间的距离；

(2)、当影子一部分在水平地面 $B C$ 上，一部分在斜坡 $C D$ 上（图2），求此时标尺与路灯间的距离为多少米？

查看试题解析

24. 为了测量学校旗杆（垂直于水平地面）的高度，班里三个兴趣小组设计了三种不同的测量方案，如下表所示.

课题	测量校园旗杆的高度
测量工具	测角仪（测量角度的仪器），卷尺，平面镜等
测量小组	A组	B组	C组
测量方案示意图
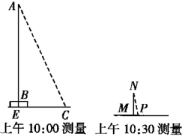
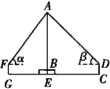
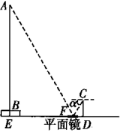
说明	线段AB表示旗杆的高度，线段BE表示旗杆底座高度，点A，B，E共线，线段CD，FG表示测角仪的高度，点A，B，C，D，E，F，G在同一竖直平面内，CG表示两次测角仪摆放位置的距离，测角仪可测得旗杆顶端A的仰角	线段AB表示旗杆的高度，线段BE表示旗杆底座高度，点A，B，E共线，线段CD表示测角仪的高度，DE表示测角仪到旗杆的距离，点F表示平面镜的中心，点E，F，D共线，眼睛在C处，移动平面镜，看向中心F，恰好看到旗杆顶端A，此时用测角仪测得平面镜的俯角，A，B，C，D，E，F六点在同一竖直平面内	线段AB表示旗杆的高度，线段BE表示旗杆底座高度，点A，B，E共线，EC为旗杆与底座某一时刻下的影长，A，B，C，E四点在同一竖直平面内，标杆NM垂直于水平地面，PM为标杆NM在某一时刻的影长
测量数据	$α$ 为 $53 °$ ， $β$ 为 $45 °$ ， $C D = F G = 1.5$ 米， $B E = 0.5$ 米， $C G = 14.79$ 米	$D E = 6.61$ 米， $C D = 1.5$ 米， $B E = 0.5$ 米， $α$ 为 $60 °$	$C E = 4.66$ 米， $M N = 1$ 米， $M P = 0.21$ 米， $B E = 0.5$ 米

(1)、上述A，B，C三个小组中，用哪个小组测量的数据计算出的旗杆高度不是旗杆的真实高度，为什么？

(2)、请结合所学知识，利用A组测量的数据计算出旗杆的高度AB.（结果保留两位小数.参考数据：

t a n 53 ° \approx \frac{4}{3}

，

\sqrt{3} \approx 1.732

）

查看试题解析