(B卷)第二章 直线与圆的位置关系-浙教版数学九年级下册单元测试
试卷更新日期:2023-09-10 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC,BD分别与⊙O切于点C,D,延长AC,BD交于点P.若 , ⊙O的半径为6cm,则图中的长为( )

 A、π cm B、2π cm C、3π cm D、4π cm2. 如图,已知AB是半圆O的直径,点C,D将分成相等的三段弧,点M在的延长线上,连接 . 对于下列两个结论,判断正确的是( )
A、π cm B、2π cm C、3π cm D、4π cm2. 如图,已知AB是半圆O的直径,点C,D将分成相等的三段弧,点M在的延长线上,连接 . 对于下列两个结论,判断正确的是( )
结论I:若 , 则为半圆O的切线;
结论II:连接 , 则
A、I和II都对 B、I对II错 C、I错II对 D、I和II都错3. 如图,矩形ABCD中,G是BC的中点,过A、D、G三点的⊙O与边AB、CD分别交于点E、点F,给出下列判断:(1)AC与BD的交点是⊙O的圆心;(2)AF与DE的交点是⊙O的圆心;(3)AE=DF;(4)BC与⊙O相切,其中正确判断的个数是( ) A、4 B、3 C、2 D、14. 如图,分别与⊙O相切于E、F、G三点,且 , cm,cm,则的长等于( )
A、4 B、3 C、2 D、14. 如图,分别与⊙O相切于E、F、G三点,且 , cm,cm,则的长等于( ) A、7cm B、6cm C、5cm D、11cm5. 《数书九章》是我国南宋时期杰出数学家秦九韶的著作,书中提出了已知三角形三边a,b,c求面积的公式.若三角形的三边a,b,c分别为7,6,3,则这个三角形内切圆的半径是( )A、 B、 C、 D、6. 如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )
A、7cm B、6cm C、5cm D、11cm5. 《数书九章》是我国南宋时期杰出数学家秦九韶的著作,书中提出了已知三角形三边a,b,c求面积的公式.若三角形的三边a,b,c分别为7,6,3,则这个三角形内切圆的半径是( )A、 B、 C、 D、6. 如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )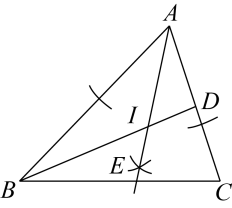 A、I到AB,AC边的距离相等 B、CI平分∠ACB C、I是△ABC的内心 D、I到A,B,C三点的距离相等7. 如图,直线 与x轴、y 轴分别相交于点A、B两点,圆心P的坐标为(2,0).⊙P与y轴相切于点O,若将⊙P沿x轴向左移动,当⊙P与该直线相交时,横坐标为整数的点P的个数是( )
A、I到AB,AC边的距离相等 B、CI平分∠ACB C、I是△ABC的内心 D、I到A,B,C三点的距离相等7. 如图,直线 与x轴、y 轴分别相交于点A、B两点,圆心P的坐标为(2,0).⊙P与y轴相切于点O,若将⊙P沿x轴向左移动,当⊙P与该直线相交时,横坐标为整数的点P的个数是( )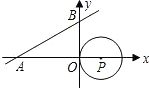 A、5 B、6 C、7 D、88. 如图所示,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(﹣3,0),B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
A、5 B、6 C、7 D、88. 如图所示,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(﹣3,0),B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )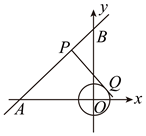 A、 B、2.4 C、 D、39. 如图所示,在Rt 中, , , ,点 为 上的点, 的半径 ,点 是 边上的动点,过点 作⊙ 的一条切线 (点 为切点),则线段 的最小值为( )
A、 B、2.4 C、 D、39. 如图所示,在Rt 中, , , ,点 为 上的点, 的半径 ,点 是 边上的动点,过点 作⊙ 的一条切线 (点 为切点),则线段 的最小值为( ) A、
A、 B、
C、
D、4
10. 如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10=( )
B、
C、
D、4
10. 如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10=( ) A、4π B、3π C、2π D、π
A、4π B、3π C、2π D、π二、填空题(每空3分,共18分)
-
11. 如图,将正方形 绕点 按逆时针方向旋转30°得到正方形 ,已知 交 于点 , ,则四边形 的内切圆半径为 .
 12. 如图,在△ABC中,AC:BC:AB=5:12:13,⊙O在△ABC内自由移动,若⊙O的半径为1,且圆心O在△ABC内所能到达的区域的面积为 ,则△ABC的周长为.
12. 如图,在△ABC中,AC:BC:AB=5:12:13,⊙O在△ABC内自由移动,若⊙O的半径为1,且圆心O在△ABC内所能到达的区域的面积为 ,则△ABC的周长为.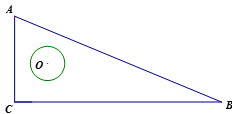 13. 如图, 是 的直径, 直线 与 相切于点 ,且 在直线 上取一点 ,连结 交 于点 若 ,则 的长是.
13. 如图, 是 的直径, 直线 与 相切于点 ,且 在直线 上取一点 ,连结 交 于点 若 ,则 的长是. 14. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AC=5,BC=12,点P是线段CD上一动点,当半径为4的⊙P与△ABC的一边相切时,CP的长为.
14. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AC=5,BC=12,点P是线段CD上一动点,当半径为4的⊙P与△ABC的一边相切时,CP的长为.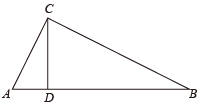 15. 如图,在△ABC中,I是△ABC的内心,O是AB边上一点,⊙O经过点B且与AI相切于点I,若tan∠BAC= , 则sin∠ACB的值为 .
15. 如图,在△ABC中,I是△ABC的内心,O是AB边上一点,⊙O经过点B且与AI相切于点I,若tan∠BAC= , 则sin∠ACB的值为 . 16. 如图,点I为△ABC的内心,连AI交△ABC的外接圆于点D,若 , 点E为弦AC的中点,连接EI,IC,若 , , 则IE的长为 .
16. 如图,点I为△ABC的内心,连AI交△ABC的外接圆于点D,若 , 点E为弦AC的中点,连接EI,IC,若 , , 则IE的长为 .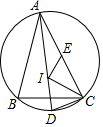
三、解答题(共9题,共72分)
-
17. 如图,是的直径,是上异于的点.外的点在射线上,直线与垂直,垂足为 , 且 . 设的面积为的面积为 .
 (1)、判断直线与的位置关系,并证明你的结论;(2)、若 , 求常数的值.18. 如图,在菱形中,对角线相交于点经过两点,交对角线于点 , 连接交于点 , 且 .
(1)、判断直线与的位置关系,并证明你的结论;(2)、若 , 求常数的值.18. 如图,在菱形中,对角线相交于点经过两点,交对角线于点 , 连接交于点 , 且 . (1)、求证:是的切线;(2)、已知的半径与菱形的边长之比为 , 求的值.19. 已知开口向上的抛物线 与直线:y=ax+c,y=cx+a中的每一条都至多有一个公共点.(1)、求 的最大值;(2)、当 取最大值时,设直线 交抛物线 于A,B两点,C为抛物线的顶点,若△ABC内切圆的半径为1,求a的值.20. 如图,已知点D在⊙O的直径延长线上,点C为⊙O上,过D作 , 与的延长线相交于E,为⊙O的切线,.
(1)、求证:是的切线;(2)、已知的半径与菱形的边长之比为 , 求的值.19. 已知开口向上的抛物线 与直线:y=ax+c,y=cx+a中的每一条都至多有一个公共点.(1)、求 的最大值;(2)、当 取最大值时,设直线 交抛物线 于A,B两点,C为抛物线的顶点,若△ABC内切圆的半径为1,求a的值.20. 如图,已知点D在⊙O的直径延长线上,点C为⊙O上,过D作 , 与的延长线相交于E,为⊙O的切线,. (1)、求证:;(2)、求的长;(3)、若的平分线与⊙O交于点F,P为的内心,求的长.21. 如图,、是的切线,、是切点,是的直径,连接 , 交于点 , 交于点 .
(1)、求证:;(2)、求的长;(3)、若的平分线与⊙O交于点F,P为的内心,求的长.21. 如图,、是的切线,、是切点,是的直径,连接 , 交于点 , 交于点 . (1)、求证:;(2)、若恰好是的中点,且四边形的面积是 , 求阴影部分的面积;(3)、若 , 且 , 求切线的长.22. CA、CB为⊙O的切线,切点分别为点A、B,延长AO交⊙O于点D,连接AB、CO,AB与CO交于点M,
(1)、求证:;(2)、若恰好是的中点,且四边形的面积是 , 求阴影部分的面积;(3)、若 , 且 , 求切线的长.22. CA、CB为⊙O的切线,切点分别为点A、B,延长AO交⊙O于点D,连接AB、CO,AB与CO交于点M, (1)、如图1,求证:∠ACB=2∠BAO;(2)、如图2,连接BD,求证:BD=2OM;(3)、如图3,在(2)的条件下,F为OD上一点,连接FM并延长交AC于点H,连接BH,若DF=2OF,HM=3,tan∠ACB= ,求线段BH的长。23. 如图,点A,B,C在上运动,满足 , 延长至点D,使得 , 点E是弦上一动点(不与点A,C重合),过点E作弦的垂线,交于点F,交的延长线于点N,交于点M(点M在劣弧上).
(1)、如图1,求证:∠ACB=2∠BAO;(2)、如图2,连接BD,求证:BD=2OM;(3)、如图3,在(2)的条件下,F为OD上一点,连接FM并延长交AC于点H,连接BH,若DF=2OF,HM=3,tan∠ACB= ,求线段BH的长。23. 如图,点A,B,C在上运动,满足 , 延长至点D,使得 , 点E是弦上一动点(不与点A,C重合),过点E作弦的垂线,交于点F,交的延长线于点N,交于点M(点M在劣弧上).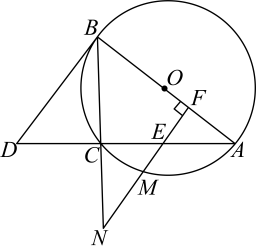 (1)、是的切线吗?请作出你的判断并给出证明;(2)、记的面积分别为 , 若 , 求的值;(3)、若的半径为1,设 , , 试求y关于x的函数解析式,并写出自变量x的取值范围.24. 请阅读以下材料,并完成相应的任务
(1)、是的切线吗?请作出你的判断并给出证明;(2)、记的面积分别为 , 若 , 求的值;(3)、若的半径为1,设 , , 试求y关于x的函数解析式,并写出自变量x的取值范围.24. 请阅读以下材料,并完成相应的任务【阅读材料】在《阿基米德全集》中的《引理集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的六个有关圆的引理,其中第二个引理是:
如图1,点P是弧的任意一点,于点C,点D在弦上且 , 在弧上取一点Q,使弧=弧 , 连接 , 则有.
 (1)、如图2,小明同学尝试说明“”,于是他连接了 , , , , 请根据小明的思路完成后续证明过程;(2)、如图3,以为直径的半圆上有一点P, , 直线l与相切于点P,过点于点E,交于点Q,求出的长.25. 阅读材料:
(1)、如图2,小明同学尝试说明“”,于是他连接了 , , , , 请根据小明的思路完成后续证明过程;(2)、如图3,以为直径的半圆上有一点P, , 直线l与相切于点P,过点于点E,交于点Q,求出的长.25. 阅读材料:在平面直角坐标系xOy中,点P(x0,y0)到直线Ax+By+C=0的距离公式为: .
例如:求点P0(0,0)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知,A=4,B=3,C=﹣3,∴点P0(0,0)到直线4x+3y﹣3=0的距离为 = .
根据以上材料,解决下列问题:
(1)、问题1:点P1(3,4)到直线 的距离为 ;(2)、问题2:已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线 相切,求实数b的值;(3)、问题3:如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出S△ABP的最大值和最小值.