（提升卷）2.3三角形的内切圆-2023-2024年浙教版数学九年级下册同步测试

试卷更新日期：2023-09-10 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图所示，已知⊙I是△ABC的内切圆，点I是内心，若∠A＝35°，则∠BIC等于（）

A、35° B、70° C、145° D、107.5°

查看试题解析
2. 如图，点 $I$ 为 $△ A B C$ 的内心，连接 $A I$ 并延长交 $△ A B C$ 的外接圆于点 $D$ ，交 $B C$ 于点 $E$ ，若 $A I = 2 C D$ ，则 $\frac{A E}{E D}$ 的值为（）

A、5 B、6 C、7 D、8

查看试题解析
3. 如图，点 $I$ 为 $△ A B C$ 的内心，连接 $A I$ 并延长，交 $△ A B C$ 的外接圆于点 $D$ ，点 $E$ 为弦 $A C$ 的中点，连接 $C D$ ， $E I$ ， $I C$ ，当 $A I = 2 C D$ ， $I C = 6$ ， $I D = 5$ 时， $I E$ 的长为（）

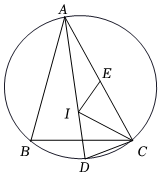A、5 B、4.5 C、4 D、3.5

查看试题解析
4. 直角三角形的外接圆半径为3，内切圆半径为1，则该直角三角形的周长是（）

A、12 B、14 C、16 D、18

查看试题解析
5. 点 $O$ 是 $△ A B C$ 的外心，也是 $△ B C D$ 的内心，若 $∠ A = 70 °$ ，则 $∠ B D C$ 的度数是（）

A、80° B、90° C、100° D、110°

查看试题解析
6. 已知在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $M$ 是 $B C$ 的中点， $B C$ 的延长线上的点 $N$ 满足 $A M ⊥ A N$ . $△ A B C$ 的内切圆与边 $A B$ ， $A C$ 的切点分别为 $E$ ， $F$ ，延长 $E F$ 分别与 $A N$ ， $B C$ 的延长线交于 $P$ ， $Q$ ，则 $\frac{P N}{Q N} =$ （）

A、0.5 B、1 C、1.5 D、2

查看试题解析
7. 以下命题：
①三角形的内心是三角形三边中垂线的垂点；②任意三角形都有且只有一个外接圆；③圆周角相等，则弧相等.④经过两点有且只有一个圆，其中真命题的个数为（）个.

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，已知矩形 $A B C D$ 的周长为 $16$ ， $⊙ E$ 和 $⊙ F$ 分别为 $Δ A B C$ 和 $Δ A D C$ 的内切圆，连接 $A E$ ， $C E$ ， $A F$ ， $C F$ ， $E F$ ，若 $\frac{S_{四边形 A E C F}}{S_{矩形 A B C D}} = \frac{3}{7}$ ，则 $E F$ 的长为（）

A、 $3 \sqrt{2}$ B、 $2 \sqrt{3}$ C、 $2 \sqrt{7}$ D、 $4 \sqrt{3}$

查看试题解析
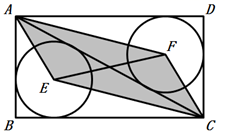9. 《九章算术》中有这样一个问题：“今有勾八步，股十五步，问勾中容圆径几何?”其意思是：“直角三角形中，勾(短直角边)长为8步，股(长直角边)长为15步，求直角三角形能容纳的圆形(内切圆)直径”。则该圆的直径为（）

A、3步 B、5步 C、6步 D、8步

查看试题解析
10. 若四边形A鱿O的对角线AC，BD相交于O，△AOB，△BOC，△COD，△DOA的周长相等，且△AOB，△BOC，△COD的内切圆半径分别为3，4，6，则△DOA的内切圆半径是（ )

A、 $\frac{9}{2}$ B、 $\frac{3}{2}$ C、 $\frac{7}{2}$ D、以上答案均不正确

查看试题解析

二、填空题（每空4分，共24分）

11. 如图，在Rt△ABC中，∠A=90°，⊙O是它的内切圆，分别切AB，BC，CA于点D， E，F．若∠ACB=40°，则∠DOE=度．

查看试题解析
12. 若三角形的面积是24cm² ，周长是24cm，则这个三角形内切圆的半径是 cm．

查看试题解析
13. 如图，已知⊙O为△ABC的内切圆，∠C=90°，BO的延长线交AC于点D，若BC=3，CD=1，则△ABC的周长为.

查看试题解析
14. 如图所示，三角形ABC中，AC＝6cm，BC＝8cm，AB＝10cm，则它的内切圆半径为 cm.

查看试题解析
15. 如图， $△ A B C$ 中， $∠ B A C = 90^{°} ， ∠ B = 40^{°}$ ， $B C$ 边上有一点P（不与点 $B ， C$ 重合），I为 $△ A P C$ 的内心，若 $∠ A I C$ 的取值范围为 $m^{°} < ∠ A I C < n^{°}$ ，则 $m + n =$ .

查看试题解析
16. 如图，点O是△ABC的内心，AO的延长线交△ABC的外接圆于点D，交BC于点E，设 $\frac{A B + A C}{B C}$ ＝a，则 $\frac{O E}{D E}$ ＝.（用含a的代数式表示）

查看试题解析

三、解答题（共8题，共66分）

17. 如图，在 $6 \times 6$ 的正方形网格中，有部分网格线被擦去.点 $A$ ， $B$ ， $C$ 在格点（正方形网格的交点）上.

(1)、请用无刻度的直尺在图1中找到三角形 $A B C$ 的外心 $P$ ；

(2)、请用无刻度的直尺在图2中找到三角形 $A B C$ 的内心 $Q$ .

查看试题解析
18. 图，在 $△ A B C$ 中，AB＝AC，⊙O是 $△ A B C$ 的外接圆，点D在⊙O上且∠BCD＝∠ACB，连接AD交BC于点E，延长DC至点F，使CF＝AC，连接AF.

(1)、求证：AF是⊙O的切线；

(2)、若点G是 $△ A C D$ 的内心， $B C \cdot B E = 25$ ，求BG的长.

查看试题解析
19. 如图，在△ABC中，E是内心，AE的延长线和△ABC的外接圆相交于点D.

(1)、求证：DB=DC；

(2)、若AB=AC，∠BAC=80°，AD=3.求 $\overset{⌢}{A B}$ 的长.

查看试题解析
20. 在平面直角坐标系中，边长为1的正方形OABC的两个顶点A，C分别在y轴、x轴的正半轴上，点O是原点.现在将正方形OABC绕原点O顺时针旋转，当点A第一次落在直线y=x上时停止.旋转过程中，AB边交直线y=x于点M，BC边交x轴于点Ｎ。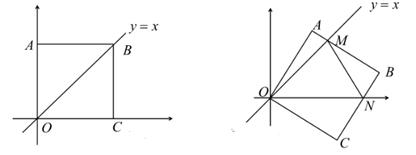

(1)、若点A（ $\frac{1}{2}$ ，b），求此时点C的坐标及b的值

(2)、若△MNB的周长是p，在旋转过程中，p值是否会发生变化？若不变，请求出这个定值，若有变化，请说明理由；

(3)、设MN=m，当m为何值时△OMN的面积最小，最小值是多少？并直接写出此时△MNB内切圆半径。

查看试题解析
21. 如图

(1)、如图1， $Δ A B C$ 的内切圆与边 $A B$ ， $A C$ ， $B C$ 分别相切于点 $D ， E ， F$ ，若 $∠ A C B = 90 °$ ， $A D = 3$ ， $B D = 4$ ，求 $Δ A B C$ 的面积 $S$ ；

(2)、观察（1）中所得结论中 $S$ 与 $A D$ ， $B D$ 之间的数量关系，猜测：若（1）中 $A D = m$ ， $B D = n$ ，其余条件不变，则 $Δ A B C$ 的面积为多少？并证明你的结论；

(3)、如图2，锐角 $Δ A B C$ 的内切圆与边 $A B ， A C ， B C$ 分别相切于点 $D ， E ， F$ ，若 $∠ A C B = 60^{\circ}$ ， $A D = m$ ， $B D = n$ ，求 $Δ A B C$ 的面积.（结果用含 $m ， n$ 的式子表示）

查看试题解析
22. 已知：△ABC内接于⊙O，∠BAC的角平分线AD交⊙O于点D.

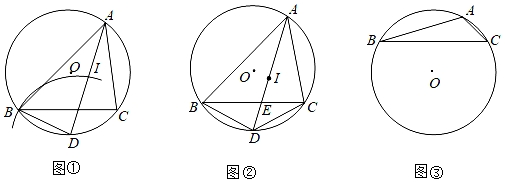(1)、如图①，以点D为圆心，DB长为半径作弧，交AD于点I.求证：点I是△ABC的内心；

(2)、如图②，在（1）的条件下，若AD与BC交于点E.求证： $\frac{D I}{D E} = \frac{C A}{C E}$ ；

(3)、探究：如图③，△ABC内接于⊙O，若BC＝8，∠BAC＝120°，求△ABC内切圆半径的最大值.

查看试题解析
23. 我们引入如下概念，
定义；到三角形的两条边的距离相等的点，叫做此三角形的准内心，举例：如图1，PE⊥BC，若PE＝PD则P为△ABC的准内心

(1)、填空；根据准内心的概念，图1中的点P在∠BAC的上．

(2)、应用；如图2，△ABC中，AC＝BC＝13，AB＝10，准内心P在AB上，求P到AC边的距离PD的长．

(3)、探究；已知△ABC为直角三角形，AC＝BC＝6，∠C＝90°，准内心P在△ABC的边上，试探究PC的长．

查看试题解析
24. 有一组邻边相等且对角互补的四边形叫做等邻边互补四边形.

(1)、如图1，在等邻边互补四边形ABCD中，AD=CD，且AD//BC， BC=2AD，求∠B的度数；

(2)、如图2，四边形ABCD内接于圆O，连结DO交AC于点E (不与点O重合)，若E是AC的中点，求证：四边形ABCD是等邻边互补四边形；

(3)、在(2) 的条件下，延长DO交BC于点F，交圆0于点G，若弧BG=弧AB， tan∠ABC= $\frac{24}{7}$ ，AC=12，求FG的长；

(4)、如图3，四边形ABCD内接于圆O，AB=BC， BD为圆0的直径，连结AO并延长交BC于点E，交圆0于点F，连结FC，设tan∠BAF=x， $\frac{E F}{A E} = y$ ，求y与x之间的函数关系式.

查看试题解析