(培优卷)2.3三角形的内切圆-2023-2024年浙教版数学九年级下册同步测试
试卷更新日期:2023-09-10 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,在 中, 其周长为20,⊙I是 的内切圆,其半径为 ,则 的外接圆半径为( )
 A、7 B、 C、 D、2. 在中, , 下列说法错误的是( )A、 B、 C、内切圆的半径 D、当时,是直角三角形3. 如图,在正中,D,E分别在边 , 上,连接 , 的平分线过的内心O,交于点F,连接 . 若要知道的周长,则只需要知道下列哪个三角形的周长?该三角形是( )
A、7 B、 C、 D、2. 在中, , 下列说法错误的是( )A、 B、 C、内切圆的半径 D、当时,是直角三角形3. 如图,在正中,D,E分别在边 , 上,连接 , 的平分线过的内心O,交于点F,连接 . 若要知道的周长,则只需要知道下列哪个三角形的周长?该三角形是( ) A、 B、 C、 D、4. 如图,是的内切圆, , 过点I作分别交 , 于N,M,若 , , 则的半径是( )
A、 B、 C、 D、4. 如图,是的内切圆, , 过点I作分别交 , 于N,M,若 , , 则的半径是( )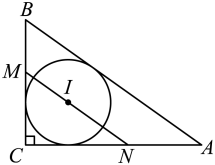 A、 B、 C、 D、5. 如图,不等边内接于 , I是其内心, , , , 内切圆半径为( )
A、 B、 C、 D、5. 如图,不等边内接于 , I是其内心, , , , 内切圆半径为( ) A、4 B、 C、 D、6. 如图, , 分别为的切线,切点为A,B,点C为弧上一动点,过点C作的切线,分别交 , 于点D,E,作的内切圆 , 若 , 的半径为R,的半径为r,则的面积是( )
A、4 B、 C、 D、6. 如图, , 分别为的切线,切点为A,B,点C为弧上一动点,过点C作的切线,分别交 , 于点D,E,作的内切圆 , 若 , 的半径为R,的半径为r,则的面积是( ) A、 B、 C、 D、7. 如图,点E为 的内心,过点 作 交 于点 ,交 于点 ,若 , , ,则MN的长为( )
A、 B、 C、 D、7. 如图,点E为 的内心,过点 作 交 于点 ,交 于点 ,若 , , ,则MN的长为( ) A、3.5 B、4 C、5 D、5.58. 如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H。设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为( )
A、3.5 B、4 C、5 D、5.58. 如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H。设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为( )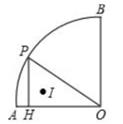 A、 B、 C、 D、π9. 如图, 中, , , ,点 在 内,且 平分 , 平分 ,过点D作直线 ,分别交 、 于点P、Q,若 与 相似,则线段 的长为( )
A、 B、 C、 D、π9. 如图, 中, , , ,点 在 内,且 平分 , 平分 ,过点D作直线 ,分别交 、 于点P、Q,若 与 相似,则线段 的长为( ) A、5 B、 C、5或 D、610. 课本中有这样一句话:“利用勾股定理,可以作出 , , , …的线段(如图).”记 , , …,的内切圆的半径分别为 , , …, , 若 , 则n的值是( )
A、5 B、 C、5或 D、610. 课本中有这样一句话:“利用勾股定理,可以作出 , , , …的线段(如图).”记 , , …,的内切圆的半径分别为 , , …, , 若 , 则n的值是( ) A、24 B、25 C、26 D、27
A、24 B、25 C、26 D、27二、填空题(每空4分,共24分)
-
11. 已知内接于⊙O,I是的内心,若 , 则的度数是.12. 如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接 , , , 当时,.
 13. 如题图所示,在中存在一面积为的内切圆,其圆心为点 , 连接 , 若满足 , , , 则实数的值为 .
13. 如题图所示,在中存在一面积为的内切圆,其圆心为点 , 连接 , 若满足 , , , 则实数的值为 . 14. 如图上,O为内心,过点O的直线分别与AC、AB相交于D、E,若DE=CD+BE,则线段CD的长为.
14. 如图上,O为内心,过点O的直线分别与AC、AB相交于D、E,若DE=CD+BE,则线段CD的长为. 15. 如图,已知 的半径为2,弦 ,点 为优弧 上动点,点 为 的内心,当点 从点 向点 运动时,点 移动的路径长为.
15. 如图,已知 的半径为2,弦 ,点 为优弧 上动点,点 为 的内心,当点 从点 向点 运动时,点 移动的路径长为. 16. 如图,扇形AOB,且OB=4,∠AOB=90°,C为弧AB上任意一点,过C点作CD⊥OB于点D,设△ODC的内心为E,连接OE、CE,当点C从点B运动到点A时,内心E所经过的路径长为 。
16. 如图,扇形AOB,且OB=4,∠AOB=90°,C为弧AB上任意一点,过C点作CD⊥OB于点D,设△ODC的内心为E,连接OE、CE,当点C从点B运动到点A时,内心E所经过的路径长为 。
三、解答题(共8题,共66分)
-
17. 如图,在平面直角坐标系中,一次函数的图象分别交x轴,y轴正半轴于点A,B,内切于 , 反比例函数的图象经过点P,交直线于点C,D(C在点D的左侧).
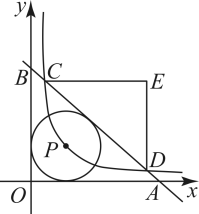 (1)、求反比例函数的解析式;(2)、过点C,D分别作x轴,y轴的平行线交于点E,求的面积.18. 如图,点E是的内心,的延长线和的外接圆相交于点D.
(1)、求反比例函数的解析式;(2)、过点C,D分别作x轴,y轴的平行线交于点E,求的面积.18. 如图,点E是的内心,的延长线和的外接圆相交于点D.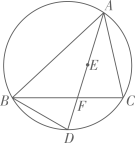 (1)、求证:;(2)、已知 , , 求该圆的半径的长度;(3)、在(2)的条件下,若 , 求的值.19. 如图,在矩形ABCD中, 为矩形 对角线, 于点 , 的延长线交AB于点E,已知 , .
(1)、求证:;(2)、已知 , , 求该圆的半径的长度;(3)、在(2)的条件下,若 , 求的值.19. 如图,在矩形ABCD中, 为矩形 对角线, 于点 , 的延长线交AB于点E,已知 , . (1)、求AE的长;(2)、 的角平分线CF交AD于点F,求 的值;(3)、若 、 分别是 、 的内心,求 、 两点间的距离.20. 如图,在△ABC中,∠ACB=90°,∠ABC=45°,BC=12cm,半圆O的直径DE=12cm.点E与点C重合,半圆O以2cm/s的速度从左向右移动,在运动过程中,点D、E始终在BC所在的直线上.设运动时间为x(s),半圆O与△ABC的重叠部分的面积为S(cm2).
(1)、求AE的长;(2)、 的角平分线CF交AD于点F,求 的值;(3)、若 、 分别是 、 的内心,求 、 两点间的距离.20. 如图,在△ABC中,∠ACB=90°,∠ABC=45°,BC=12cm,半圆O的直径DE=12cm.点E与点C重合,半圆O以2cm/s的速度从左向右移动,在运动过程中,点D、E始终在BC所在的直线上.设运动时间为x(s),半圆O与△ABC的重叠部分的面积为S(cm2). (1)、当x=0时,设点M是半圆O上一点,点N是线段AB上一点,则MN的最大值为 :MN的最小值为.(2)、在平移过程中,当点O与BC的中点重合时,求半圆O与△ABC重叠部分的面积S;(3)、当x为何值时,半圆O与△ABC的边所在的直线相切?21. 如图:
(1)、当x=0时,设点M是半圆O上一点,点N是线段AB上一点,则MN的最大值为 :MN的最小值为.(2)、在平移过程中,当点O与BC的中点重合时,求半圆O与△ABC重叠部分的面积S;(3)、当x为何值时,半圆O与△ABC的边所在的直线相切?21. 如图: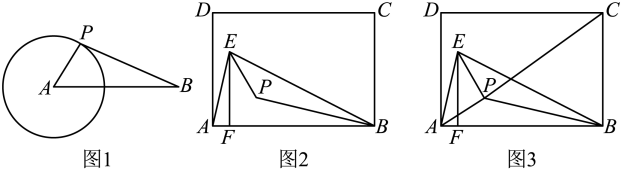 (1)、如图1,的半径为2, , 点为上任意一点,则的最小值为 .(2)、如图2,已知矩形 , 点为上方一点,连接 , , 作于点 , 点是的内心,求的度数.(3)、如图3,在(2)的条件下,连接 , , 若矩形的边长 , , , 求此时的最小值.22. 已知:△ABC内接于⊙O,∠BAC的角平分线AD交⊙O于点D.
(1)、如图1,的半径为2, , 点为上任意一点,则的最小值为 .(2)、如图2,已知矩形 , 点为上方一点,连接 , , 作于点 , 点是的内心,求的度数.(3)、如图3,在(2)的条件下,连接 , , 若矩形的边长 , , , 求此时的最小值.22. 已知:△ABC内接于⊙O,∠BAC的角平分线AD交⊙O于点D.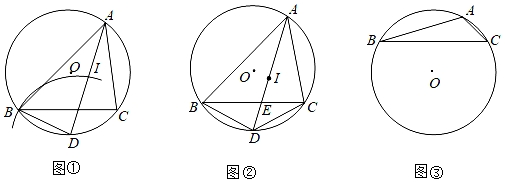 (1)、如图①,以点D为圆心,DB长为半径作弧,交AD于点I.求证:点I是△ABC的内心;(2)、如图②,在(1)的条件下,若AD与BC交于点E.求证:;(3)、探究:如图③,△ABC内接于⊙O,若BC=8,∠BAC=120°,求△ABC内切圆半径的最大值.23. 【阅读材料】已知,如图1,在面积为S的△ABC中,BC=a,AC=b,AB=c,内切圆O的半径为r,连接OA,OB,OC,△ABC被划分为三个小三角形.
(1)、如图①,以点D为圆心,DB长为半径作弧,交AD于点I.求证:点I是△ABC的内心;(2)、如图②,在(1)的条件下,若AD与BC交于点E.求证:;(3)、探究:如图③,△ABC内接于⊙O,若BC=8,∠BAC=120°,求△ABC内切圆半径的最大值.23. 【阅读材料】已知,如图1,在面积为S的△ABC中,BC=a,AC=b,AB=c,内切圆O的半径为r,连接OA,OB,OC,△ABC被划分为三个小三角形.∵S=S△OBC+S△OAC+S△OAB=BC•r+AC•r+AB•r=ar+br+cr=(a+b+c)r.
∴r= .
(1)【类比推理】如图2,若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
(2)【理解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC各边分别相切于D、E和F,已知AD=3,BD=2,求r的值.
 24. 我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设, ,为三角形三边, 为面积,则 ①
24. 我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设, ,为三角形三边, 为面积,则 ①这是中国古代数学的瑰宝之一.
而在文明古国古希腊,也有一个数学家海伦给出了求三角形面积的另一个公式,若设 (周长的一半),则 ②
(1)、尝试验证.这两个公式在表面上形式很不一致,请你用以5,7,8为三边构成的三角形,分别验证它们的面积值;(2)、问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从① ②或者② ① ;(3)、问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图, 的内切圆半径为,三角形三边长为, ,仍记 , 为三角形面积,则 .