(培优卷)2.2切线长定理-2023-2024年浙教版数学九年级下册同步测试
试卷更新日期:2023-09-10 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,在四边形中, , 以为圆心,为半径的弧恰好与相切,切点为 . 若 , 则的值是( )
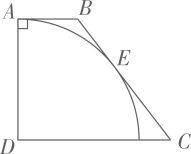 A、 B、 C、 D、2. 如图,将直尺、含的直角三角尺和量角器按如图摆放,角的顶点A在直尺上读数为4,量角器与直尺的接触点B在直尺上的读数为7,量角器与直角三角尺的接触点为点C,则该量角器的直径是( ).
A、 B、 C、 D、2. 如图,将直尺、含的直角三角尺和量角器按如图摆放,角的顶点A在直尺上读数为4,量角器与直尺的接触点B在直尺上的读数为7,量角器与直角三角尺的接触点为点C,则该量角器的直径是( ). A、3 B、 C、6 D、3. 如图是个一不倒的主视图,不倒翁的圆形脸恰好与帽子边沿 , 分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若 , 则的度数为( ).
A、3 B、 C、6 D、3. 如图是个一不倒的主视图,不倒翁的圆形脸恰好与帽子边沿 , 分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若 , 则的度数为( ). A、 B、 C、 D、4. 如图,的内切圆与、、分别相切于点、、 , 且 , , , 则阴影部分(即四边形)的面积是( )
A、 B、 C、 D、4. 如图,的内切圆与、、分别相切于点、、 , 且 , , , 则阴影部分(即四边形)的面积是( ) A、4 B、6.25 C、7.5 D、95. 如图,中, , , 以BC边上一点O为圆心作 , 分别与AB,AC相切于点D,E,则AD的长为( )
A、4 B、6.25 C、7.5 D、95. 如图,中, , , 以BC边上一点O为圆心作 , 分别与AB,AC相切于点D,E,则AD的长为( ) A、4.5 B、5 C、5.5 D、66. 如图,以正方形的边为直径作半圆O过点C作直线切半圆于点F,交边于点E,若的周长为12,则线段的长为( )
A、4.5 B、5 C、5.5 D、66. 如图,以正方形的边为直径作半圆O过点C作直线切半圆于点F,交边于点E,若的周长为12,则线段的长为( ) A、1 B、2 C、 D、7. 如图,、分别与相切于点、 , 连接并延长与交于点、 , 若 , , 则的值为( )
A、1 B、2 C、 D、7. 如图,、分别与相切于点、 , 连接并延长与交于点、 , 若 , , 则的值为( ) A、 B、 C、 D、8. 在直角坐标系中,一次函数 的图象记作G,以原点O为圆心,作半径为1的圆,有以下几种说法:
A、 B、 C、 D、8. 在直角坐标系中,一次函数 的图象记作G,以原点O为圆心,作半径为1的圆,有以下几种说法:①当G与⊙O相交时,y随x增大而增大;②当G与⊙O相切时, ③当G与⊙O相离时, 或 . 其中正确的说法是( )
A、① B、①② C、①③ D、②③9. 如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D。下列结论不一定成立的是( )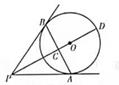 A、△BPA为等腰三角形 B、AB与PD相互垂直平分 C、点A,B都在以PO为直径的圆上 D、PC为△BPA的边AB上的中线10. 如图,⊙O内切于正方形ABCD,边AD,CD分别与⊙O切于点E,F,点M、N分别在线段DE,DF上,且MN与⊙O相切,若△MBN的面积为8,则⊙O的半径为( )
A、△BPA为等腰三角形 B、AB与PD相互垂直平分 C、点A,B都在以PO为直径的圆上 D、PC为△BPA的边AB上的中线10. 如图,⊙O内切于正方形ABCD,边AD,CD分别与⊙O切于点E,F,点M、N分别在线段DE,DF上,且MN与⊙O相切,若△MBN的面积为8,则⊙O的半径为( )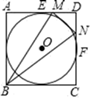 A、 B、2 C、 D、2
A、 B、2 C、 D、2二、填空题(每题3分,共18分)
-
11. 小明对《数书九章》中的“遥度圆城”问题进行了改编:如图,一座圆形城堡有正东、正南、正西和正北四个门,出南门向东走一段路程后刚好看到北门外的一颗大树,向树的方向走9里到达城堡边,再往前走6里到达树下.则该城堡的外围直径为里.
 12. 某款“不倒翁”(如图)的主视图是图 , 分别与所在圆相切于点A,B,若该圆半径是 , 则主视图的面积为 .
12. 某款“不倒翁”(如图)的主视图是图 , 分别与所在圆相切于点A,B,若该圆半径是 , 则主视图的面积为 .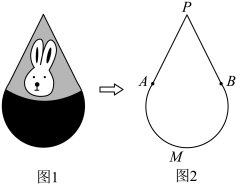 13. 如图, 在矩形 中 , 点 为 的中点, 点 为边 上的动点, 连结 . 将 沿着 翻折, 使点 的对应点 恰好落在线段 上. 若 三点共线, 则 的值为;若 , 且这样的点 有且只有一个时, 则 的长为.
13. 如图, 在矩形 中 , 点 为 的中点, 点 为边 上的动点, 连结 . 将 沿着 翻折, 使点 的对应点 恰好落在线段 上. 若 三点共线, 则 的值为;若 , 且这样的点 有且只有一个时, 则 的长为. 14. 如图,半径为2的⊙O与含有30°角的直角三角板ABC的AC边切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与⊙O相切时,该直角三角板平移的距离为.
14. 如图,半径为2的⊙O与含有30°角的直角三角板ABC的AC边切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与⊙O相切时,该直角三角板平移的距离为. 15. 如图,在△ABC中,AB=AC,在∠ABC的内部作∠ABE=45°,EC⊥BC点D在AB上,DE、AC相交点F,若以DE为直径的⊙O与AB、BC都相切,切点分别为点D和G,则 的值是.
15. 如图,在△ABC中,AB=AC,在∠ABC的内部作∠ABE=45°,EC⊥BC点D在AB上,DE、AC相交点F,若以DE为直径的⊙O与AB、BC都相切,切点分别为点D和G,则 的值是.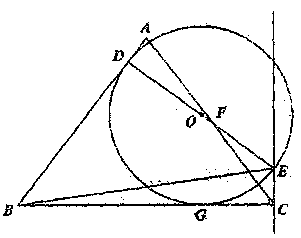 16. 如图,PA、PB分别切⊙O于A、B,点C、M是⊙O上的点,∠AMB=60°,过点C作的切线交PA、PB于E、F,△PEF的外心在PE上.已知PA=3,则AE的长为 .
16. 如图,PA、PB分别切⊙O于A、B,点C、M是⊙O上的点,∠AMB=60°,过点C作的切线交PA、PB于E、F,△PEF的外心在PE上.已知PA=3,则AE的长为 .
三、解答题(共8题,共72分)
-
17. 如图,在四边形中, , 以为直径作平分 , 动点P在左侧的半圆O上(P与点A,B均不重合).
 (1)、求证:是的切线;(2)、记(1)中的切点为E,若 , 求的值.18. 如图,已知是的直径, , 为圆上任意一点,过点作圆的切线,分别与过 , 两点的切线交于 , 两点.
(1)、求证:是的切线;(2)、记(1)中的切点为E,若 , 求的值.18. 如图,已知是的直径, , 为圆上任意一点,过点作圆的切线,分别与过 , 两点的切线交于 , 两点. (1)、求的值;(2)、如图,连接 , 交于点 , 证明直线 .
(1)、求的值;(2)、如图,连接 , 交于点 , 证明直线 . 19. 已知的半径为为的一条直径,P为外一点,且 , 过点P作的两条切线 , 连接与相交于点G.
19. 已知的半径为为的一条直径,P为外一点,且 , 过点P作的两条切线 , 连接与相交于点G. (1)、求证:;(2)、求点O到线段的距离;(3)、记线段与交于点F,连接 , 直接写出的值.20. 如图,已知是的直径, , 切于点 , 过点作交于点 , 若 .
(1)、求证:;(2)、求点O到线段的距离;(3)、记线段与交于点F,连接 , 直接写出的值.20. 如图,已知是的直径, , 切于点 , 过点作交于点 , 若 . (1)、如图1,连接 , 求证:;(2)、如图2,是上一点,在上取一点 , 使 , 连接 . 请问:三条线段有怎样的数量关系?并证明你的结论.21. 已知 的两边分别与⊙O相切于点A,B,⊙O的半径为r.
(1)、如图1,连接 , 求证:;(2)、如图2,是上一点,在上取一点 , 使 , 连接 . 请问:三条线段有怎样的数量关系?并证明你的结论.21. 已知 的两边分别与⊙O相切于点A,B,⊙O的半径为r. (1)、如图1,点C在点A,B之间的优弧上, ,则 ;(2)、如图2,点C在圆上运动,当 最大时(即连接 并延长交⊙O于点C),连接 , ,
(1)、如图1,点C在点A,B之间的优弧上, ,则 ;(2)、如图2,点C在圆上运动,当 最大时(即连接 并延长交⊙O于点C),连接 , ,①求证: ;
②若 交⊙O于另一点D, ,求图中对应的阴影部分的周长(用含r的式子表示).
22. 已知,AB是⊙O的直径,AB=16,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=10,PT为⊙O的切线,切点为T.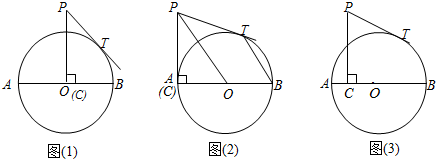 (1)、如图(1),当C点运动到O点时,求PT的长;(2)、如图(2),当C点运动到A点时,连接PO、BT,求证:PO∥BT;(3)、如图(3),设PT=y,AC=x,求y与x的解析式并求出y的最小值.23. 如图1,AC是⊙O的直径,PA是⊙O的切线,A为切点,点B在⊙O上,PA=PB,弦AB与PC交于点M
(1)、如图(1),当C点运动到O点时,求PT的长;(2)、如图(2),当C点运动到A点时,连接PO、BT,求证:PO∥BT;(3)、如图(3),设PT=y,AC=x,求y与x的解析式并求出y的最小值.23. 如图1,AC是⊙O的直径,PA是⊙O的切线,A为切点,点B在⊙O上,PA=PB,弦AB与PC交于点M (1)、求证:PB是⊙O的切线(2)、连接BC,若∠APB=4∠BPC,AP=6,求BC的长(3)、如图2,若AB=4BM,求 的值(4)、如图3,若AP=AC,PO与AB交于点D,PC与⊙O交于点N,连接DN,则 =24.
(1)、求证:PB是⊙O的切线(2)、连接BC,若∠APB=4∠BPC,AP=6,求BC的长(3)、如图2,若AB=4BM,求 的值(4)、如图3,若AP=AC,PO与AB交于点D,PC与⊙O交于点N,连接DN,则 =24. (1)、探究问题:如图1,PM、PN、EF分别切⊙O于点A、B、C,猜想△PEF的周长与切线长PA的数量关系,并证明你的结论.(2)、变式迁移:如果图1的条件不变,且PO=10厘米,△PEF的周长为16厘米,那么⊙O 的半径为厘米.(3)、拓展提高:如图2,点E是∠MPN的边PM上的点,EF⊥PN于点F,⊙O与边EF及射线PM、射线PN都相切.
(1)、探究问题:如图1,PM、PN、EF分别切⊙O于点A、B、C,猜想△PEF的周长与切线长PA的数量关系,并证明你的结论.(2)、变式迁移:如果图1的条件不变,且PO=10厘米,△PEF的周长为16厘米,那么⊙O 的半径为厘米.(3)、拓展提高:如图2,点E是∠MPN的边PM上的点,EF⊥PN于点F,⊙O与边EF及射线PM、射线PN都相切.①画出符合条件的⊙O;
②若EF=3,PF=4,求⊙O的半径.