（基础卷）2.2切线长定理-2023-2024年浙教版数学九年级下册同步测试
试卷更新日期：2023-09-10 类型：同步测试
一、选择题（每题4分，共40分）
-
1. 如图，P为⊙外一点，PA、PB分别切⊙于A、B两点，若 ， 则（ ）
A、2 B、3 C、4 D、52. 如图，AB、AC、BD是⊙O的切线，切点分别为P、C、D，若 ， ， 则BD的长是（ ）
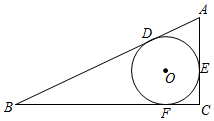
A、2.5 B、2 C、1.5 D、13. 如图，PA、PB切⊙O于点A、B，直线FG切⊙O于点E，交PA于F，交PB于点G，若PA＝8cm，则△PFG的周长是（ ）
A、8cm B、12cm C、16cm D、20cm4. 如图所示，⊙O内切于四边形ABCD，AB＝10，BC＝7，CD＝8，则AD的长度为（ ）
A、8 B、9 C、10 D、115. 如图，PA，PB是⊙O的切线，A，B是切点，点C为⊙O上一点，若∠ACB＝70°，则∠P的度数为（ ）
A、70° B、50° C、20° D、40°6. 如图，PA和PB是⊙O的切线，点A和B的切点，AC是⊙O的直径，已知∠P＝50°，则∠ACB的大小是（ ）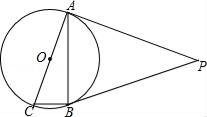
A、65° B、60° C、55° D、50°7. 如图， 分别切 与点 切 于点 ，分别交 于点 ，若 的周长 ，则 是（ ）
A、 B、 C、 D、8. 如图，AB、AC是圆O的两条切线，切点为B、C且∠BAC=50°，D是优弧BDC上一动点（不与B、C重合），则∠BDC的度数为（ ）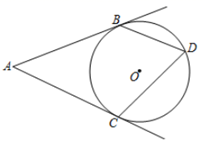
A、130° B、65° C、50°或130° D、65°或115°9. 如图PA，PB分别与 相切于A，B两点．若 ，则 的度数为（ ）
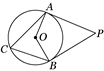A、 B、 C、 D、10. 如图，PA切⊙O于点A，PB切⊙O于点B，如果∠APB=60°，⊙O半径是3，则劣弧AB的长为（ ）
A、 B、π C、2π D、4π二、填空题（每题5分，共25分）
-
11. 如图，AB，AC，BD是⊙O的切线，P，C，D为切点，若AB=10，AC=7，则BD的长为 ．
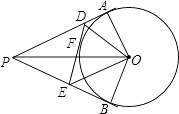
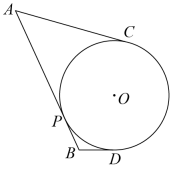12. 如图，分别过上、、三点作切线，切线两两交于、、 ， ， 则的周长为 ．
13. 如图，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径，∠BAC＝25°，则∠P的度数为 ．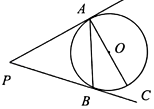
14. 如图，PA，PB分别切⊙O于点A，B，Q是优弧上一点，若∠P=40°，则∠Q的度数是 ．
15. 已知 分别切 于点 ， 为 上不同于 的一点， ，则 的度数是 ．三、解答题（共5题，共55分）
-
16. 如图，PA、PB是⊙O的两条切线，A、B是切点，AC是⊙O的直径，∠BAC＝35°，求∠P的度数．
17. 如图，AB，BC，CD分别与⊙O相切于E，F，G，且AB ∥ CD，BO=6cm，CO=8cm.求BC的长
