(提升卷)2.1 直线与圆的位置关系-2023-2024年浙教版数学九年级下册同步测试
试卷更新日期:2023-09-10 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 在平面直角坐标系中,点P的坐标为(3,m),若OP与y轴相切,那么⨀P与直线x=5的位置关系是( )A、相交 B、相切 C、相离 D、不能确定2. 如图,在平行四边形ABCD中, , , 以顶点C为圆心,BC为半径作圆,则AD边所在直线与的位置关系是( )
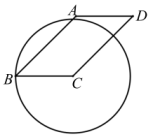 A、相交 B、相切 C、相离 D、以上三种都有可能3. 如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x , 0),若直线AB与半圆弧有公共点,则x值的范围是( )
A、相交 B、相切 C、相离 D、以上三种都有可能3. 如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x , 0),若直线AB与半圆弧有公共点,则x值的范围是( )
 A、﹣3≤x≤3 B、﹣3≤x≤3 C、﹣3 ≤x≤3 D、0≤x≤34. 如图,已知直线 与x轴、y轴分别交于B,C两点,点A是以D(0,2)为圆心,2为半径的⊙D上的一个动点,连接AC、AB,则△ABC面积的最小值是( )
A、﹣3≤x≤3 B、﹣3≤x≤3 C、﹣3 ≤x≤3 D、0≤x≤34. 如图,已知直线 与x轴、y轴分别交于B,C两点,点A是以D(0,2)为圆心,2为半径的⊙D上的一个动点,连接AC、AB,则△ABC面积的最小值是( ) A、30 B、29 C、28 D、275. 如图,在Rt△ABC中,∠C=90°,BC=4, . ⊙C的半径长为2,P是△ABC边上一动点(可以与顶点重合),并且点P到⊙C的切线长为m.若满足条件的点P有4个,则m的取值范围是( )
A、30 B、29 C、28 D、275. 如图,在Rt△ABC中,∠C=90°,BC=4, . ⊙C的半径长为2,P是△ABC边上一动点(可以与顶点重合),并且点P到⊙C的切线长为m.若满足条件的点P有4个,则m的取值范围是( ) A、 B、 C、 D、6. 如图是某款“不倒翁”的示意图, , 分别与所在圆相切于点 , . 若该圆半径是 , , 则的长是( )
A、 B、 C、 D、6. 如图是某款“不倒翁”的示意图, , 分别与所在圆相切于点 , . 若该圆半径是 , , 则的长是( )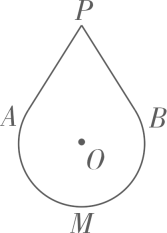 A、 B、 C、 D、7. 如图,AB是⊙O的直径,点C是AB延长线上的一点,CD与⊙O相切于点D,连接AD,BD.若∠C=30°,则( )
A、 B、 C、 D、7. 如图,AB是⊙O的直径,点C是AB延长线上的一点,CD与⊙O相切于点D,连接AD,BD.若∠C=30°,则( ) A、BC+BD=CD B、AB+BD=CD C、BC+CD=AB D、AD+AC=AB8. 如图,BC与⊙O相切于点B,CO连接并延长后交⊙O于点A,连接AB,若∠BAC=36°,则∠C的度数为( )
A、BC+BD=CD B、AB+BD=CD C、BC+CD=AB D、AD+AC=AB8. 如图,BC与⊙O相切于点B,CO连接并延长后交⊙O于点A,连接AB,若∠BAC=36°,则∠C的度数为( ) A、36° B、24° C、18° D、15°9. 如图所示,在直角坐标系中,A点坐标为 , 的半径为2,P为x轴上一动点,切于点B,则的最小值为( )
A、36° B、24° C、18° D、15°9. 如图所示,在直角坐标系中,A点坐标为 , 的半径为2,P为x轴上一动点,切于点B,则的最小值为( ) A、2 B、3 C、 D、410. 定义:在 , D,E分别是两边的中点,如果上的所有点都在的内部或边上,则称为的中内弧.如图1,是的一条中内弧,如图2,在中, , D,E分别是AB,AC的中点.则所有中内弧所组成的图形(图中阴影部分表示)为( )
A、2 B、3 C、 D、410. 定义:在 , D,E分别是两边的中点,如果上的所有点都在的内部或边上,则称为的中内弧.如图1,是的一条中内弧,如图2,在中, , D,E分别是AB,AC的中点.则所有中内弧所组成的图形(图中阴影部分表示)为( ) A、
A、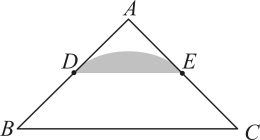 B、
B、 C、
C、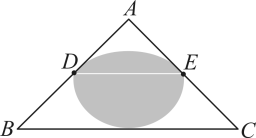 D、
D、
二、填空题(每题3分,共18分)
-
11. 已知的半径是一元二次方程的一个根,圆心O到直线l的距离 , 则直线l与的位置关系是.12. 如图,在 中, ,以C为圆心,r为半径作圆.若该圆与线段 只有一个交点,则r的取值范围为.
 13. 把量角器和含角的三角板按如图1方式摆放,将其抽象为图2:若与相切于点E, , . 则阴影部分的面积为 .
13. 把量角器和含角的三角板按如图1方式摆放,将其抽象为图2:若与相切于点E, , . 则阴影部分的面积为 . 14. 在矩形ABCD中, , , 点O在对角线AC上,圆O的半径为2,如果圆O与矩形ABCD只有一个公共点,那么线段AO的长是 .15. 如图,△ABC中,∠BAC=35° ,边BC与以AB为直径的⊙O相切于点B,将△ABC绕点A顺时针旋转,记旋转角度为a (0°<a<180),旋转过程中,△ABC 的边与⊙O相切时,a的值为.
14. 在矩形ABCD中, , , 点O在对角线AC上,圆O的半径为2,如果圆O与矩形ABCD只有一个公共点,那么线段AO的长是 .15. 如图,△ABC中,∠BAC=35° ,边BC与以AB为直径的⊙O相切于点B,将△ABC绕点A顺时针旋转,记旋转角度为a (0°<a<180),旋转过程中,△ABC 的边与⊙O相切时,a的值为. 16. 如图,点A (7 , 7),过A作AB⊥x轴于点B,C是反比例函数y=图像上一动点且在△AOB内部,以C为圆心为半径作⊙C,当⊙C与△AOB的边相切时,点C的纵坐标是 .
16. 如图,点A (7 , 7),过A作AB⊥x轴于点B,C是反比例函数y=图像上一动点且在△AOB内部,以C为圆心为半径作⊙C,当⊙C与△AOB的边相切时,点C的纵坐标是 .
三、解答题(共9题,共72分)
-
17. 如图,是由边长为1的小正方形构成的6×6网格,每个小正方形的顶点叫做格点,⊙O经过A、B、C、D四个格点,仅用无刻度的直尺在给定的网格中按要求画图(画图过程中起辅助作用的用虚线表示,画图结果用实线表示,并用黑色水笔描黑)
 (1)、如图1,判断圆心O▲ (填“是”或“不是”)在格点上,并在图1中标出格点O;(2)、在图1中画出⊙O的切线CG(G为格点);(3)、在图2中画出的中点E;18. 如图,⊙O是△ABC的外接圆,AE是⊙O的直径,点B的中点,过点B的切线与AC的延长线交于点D.
(1)、如图1,判断圆心O▲ (填“是”或“不是”)在格点上,并在图1中标出格点O;(2)、在图1中画出⊙O的切线CG(G为格点);(3)、在图2中画出的中点E;18. 如图,⊙O是△ABC的外接圆,AE是⊙O的直径,点B的中点,过点B的切线与AC的延长线交于点D.
①求证:BD⊥AD;
②若AC=9,tan∠ABC= , 求⊙O的半径.
19. 如图,公路MN和村路PQ在P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.假设拖拉机行驶时,周围100m以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,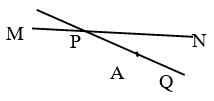 (1)、学校是否会受到噪声影响?请说明理由;(2)、如果受影响,已知拖拉机的速度为18km/h时,那么学校受影响的时间为多少秒?20. 如图在中, , 在其内部有一点 , 以为圆心,为半径的圆与相切于点交于点 , 连接交于点 .
(1)、学校是否会受到噪声影响?请说明理由;(2)、如果受影响,已知拖拉机的速度为18km/h时,那么学校受影响的时间为多少秒?20. 如图在中, , 在其内部有一点 , 以为圆心,为半径的圆与相切于点交于点 , 连接交于点 . (1)、求证: .(2)、连接 , 若 , 且 , 求的半径.21. 如图,以四边形的对角线为直径作圆,圆心为 , 过点作的延长线于点 , 已知平分 .
(1)、求证: .(2)、连接 , 若 , 且 , 求的半径.21. 如图,以四边形的对角线为直径作圆,圆心为 , 过点作的延长线于点 , 已知平分 . (1)、求证:是的切线;(2)、若 , , 求的半径和的长.22. 如图,为的直径,为弦,且于E,F为延长线上一点,恰好平分.
(1)、求证:是的切线;(2)、若 , , 求的半径和的长.22. 如图,为的直径,为弦,且于E,F为延长线上一点,恰好平分.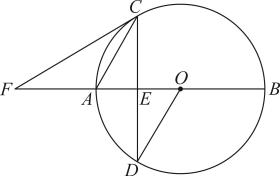 (1)、求证:与相切;(2)、连接 , 若 , 求的值.23. 如图,是的直径,是延长线上的一点,点在上, , 交的延长线于点 , 交于点 , 且是的中点.
(1)、求证:与相切;(2)、连接 , 若 , 求的值.23. 如图,是的直径,是延长线上的一点,点在上, , 交的延长线于点 , 交于点 , 且是的中点. (1)、求证:是的切线;(2)、若 , , 求的长.24. 如图,在△ABC中,∠BCA=90°,以BC为直径的⊙O交AB于点P,Q是AC的中点,连接QP并延长交CB的延长线于点D.
(1)、求证:是的切线;(2)、若 , , 求的长.24. 如图,在△ABC中,∠BCA=90°,以BC为直径的⊙O交AB于点P,Q是AC的中点,连接QP并延长交CB的延长线于点D.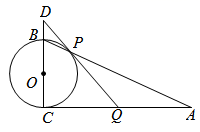 (1)、判断直线PQ与⊙O的位置关系,并说明理由:(2)、若AP=4,tanA= ,
(1)、判断直线PQ与⊙O的位置关系,并说明理由:(2)、若AP=4,tanA= ,①求⊙O的半径的长;
②求PD的长.
25. 阅读材料:
在平面直角坐标系xOy中,点P(x0 , y0)到直线Ax+By+C=0的距离公式为:d= .
例如:求点P0(0,0)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知,A=4,B=3,C=﹣3,
∴点P0(0,0)到直线4x+3y﹣3=0的距离为d= = .
根据以上材料,解决下列问题:
(1)、问题1:点P1(3,4)到直线y=﹣ x+ 的距离为;(2)、问题2:已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线y=﹣ x+b相切,求实数b的值;(3)、问题3:如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出S△ABP的最大值和最小值.