(培优卷)2.1 直线与圆的位置关系-2023-2024年浙教版数学九年级下册同步测试
试卷更新日期:2023-09-10 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 已知中, , 、 . 以C为圆心作 , 如果圆C与斜边有两个公共点,那么圆C的半径长R的取值范围是( )A、 B、 C、 D、 .2. 如图,点A的坐标是(−2,0),点C是以OA为直径的⊙B上的一动点,点A关于点C的对称点为点P.当点C在⊙B上运动时,所有这样的点P组成的图形与直线y=kx-3k(k>0)有且只有一个公共点,则k的值为( ).
 A、 B、 C、 D、3. 如图,在矩形中,对角线与相交于点 , , . 分别以点、为圆心画圆,如果与直线相交、与直线相离,且与内切,那么的半径长的取值范围是( )
A、 B、 C、 D、3. 如图,在矩形中,对角线与相交于点 , , . 分别以点、为圆心画圆,如果与直线相交、与直线相离,且与内切,那么的半径长的取值范围是( ) A、 B、 C、 D、4. 如图,在中, , 点在斜边上,以为直径的半圆与相切于点 , 与相交于点 , 连接 . 若 , , 则的长是( )
A、 B、 C、 D、4. 如图,在中, , 点在斜边上,以为直径的半圆与相切于点 , 与相交于点 , 连接 . 若 , , 则的长是( )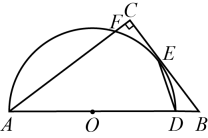 A、 B、 C、 D、5. 如图,在Rt△ABC中,∠C=90°,BC=18,AC=24,点O在边AB上,且BO=2OA . 以点O为圆心,r为半径作圆,如果⊙O与Rt△ABC的边有3个公共点,那么下列各值中,半径r不可以取的是( )
A、 B、 C、 D、5. 如图,在Rt△ABC中,∠C=90°,BC=18,AC=24,点O在边AB上,且BO=2OA . 以点O为圆心,r为半径作圆,如果⊙O与Rt△ABC的边有3个公共点,那么下列各值中,半径r不可以取的是( )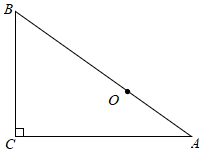 A、6 B、10 C、15 D、166. 在平面直角坐标系中,点A(﹣4,0),点B(2,0),若点C在一次函数y=﹣ 的图象上,且△ABC为直角三角形,则满足条件的点C有( )A、2个 B、3个 C、4个 D、5个7. 以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )A、0≤b<2 B、﹣2
A、6 B、10 C、15 D、166. 在平面直角坐标系中,点A(﹣4,0),点B(2,0),若点C在一次函数y=﹣ 的图象上,且△ABC为直角三角形,则满足条件的点C有( )A、2个 B、3个 C、4个 D、5个7. 以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )A、0≤b<2 B、﹣2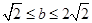 C、﹣2
C、﹣2 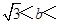 2
D、﹣2 <b<2
8. 如图,在等腰中, , BC= , 同时与边的延长线、射线相切,的半径为3.将绕点按顺时针方向旋转 , 、的对应点分别为、 , 在旋转的过程中边所在直线与相切的次数为( )
2
D、﹣2 <b<2
8. 如图,在等腰中, , BC= , 同时与边的延长线、射线相切,的半径为3.将绕点按顺时针方向旋转 , 、的对应点分别为、 , 在旋转的过程中边所在直线与相切的次数为( )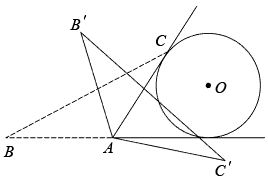 A、1 B、2 C、3 D、49. 如图,在中, , , , 点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
A、1 B、2 C、3 D、49. 如图,在中, , , , 点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )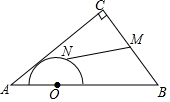 A、5 B、6 C、7 D、810. 已知在平面直角坐标系xOy中,点A的坐标为(3,4),M是抛物线(a≠0)对称轴上的一个动点,小明经探究发现:当的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定.当满足( )时,抛物线(a≠0)的对称轴上存在4个不同的点M,使△AOM为直角三角形.A、 B、 C、 D、
A、5 B、6 C、7 D、810. 已知在平面直角坐标系xOy中,点A的坐标为(3,4),M是抛物线(a≠0)对称轴上的一个动点,小明经探究发现:当的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定.当满足( )时,抛物线(a≠0)的对称轴上存在4个不同的点M,使△AOM为直角三角形.A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 在平面直角坐标系 中,以O为圆心,2个单位长度为半径画圆.若一次函数 (k为常数, )的图象与 有公共点,则k的取值范围是.12. 如图,已知射线 ,点 从B点出发,以每秒1个单位长度沿射线 向右运动;同时射线 绕点 顺时针旋转一周,当射线 停止运动时,点 随之停止运动.以 为圆心,1个单位长度为半径画圆,若运动两秒后,射线 与 恰好有且只有一个公共点,则射线 旋转的速度为每秒度.
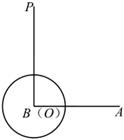 13. 如图,在四边形中, , , , 点在对角线上运动,为的外接圆,当与四边形的一边相切时,其半径为.
13. 如图,在四边形中, , , , 点在对角线上运动,为的外接圆,当与四边形的一边相切时,其半径为. 14. 如图,在矩形中, , , 点E是的中点,连接 , 点O是线段上一点,的半径为1,如果与矩形的各边都没有公共点,那么线段长的取值范围是 .
14. 如图,在矩形中, , , 点E是的中点,连接 , 点O是线段上一点,的半径为1,如果与矩形的各边都没有公共点,那么线段长的取值范围是 . 15. 图1是一款带毛刷的圆型扫地机器人,它的俯视图如图2所示,的直径为40cm,毛刷的一端为固定点 , 另一端为点 , , 毛刷绕着点旋转形成的圆弧交于点A, , 且A, , 三点在同一直线上.毛刷在旋转过程中,与交于点 , 则的最大长度为cm.扫地机器人在遇到障碍物时会自转,毛刷碰到障碍物时可弯曲.如图3,当扫地机器人在清扫角度为60°的墙角()时,不能清扫到的面积(图中阴影部分)为.
15. 图1是一款带毛刷的圆型扫地机器人,它的俯视图如图2所示,的直径为40cm,毛刷的一端为固定点 , 另一端为点 , , 毛刷绕着点旋转形成的圆弧交于点A, , 且A, , 三点在同一直线上.毛刷在旋转过程中,与交于点 , 则的最大长度为cm.扫地机器人在遇到障碍物时会自转,毛刷碰到障碍物时可弯曲.如图3,当扫地机器人在清扫角度为60°的墙角()时,不能清扫到的面积(图中阴影部分)为. 16. 如图1是一款便携式拉杆车,其侧面示意图如图2所示,前轮的直径为 , 拖盘与后轮相切于点N,手柄 . 侧面为矩形ABCD的货物置于拖盘上, , . 如图3所示,倾斜一定角度拉车时,货物绕点B旋转,点C落在上,若 , 则的长为 , 同一时刻,点C离地面高度 , 则点A离地面高度为 .
16. 如图1是一款便携式拉杆车,其侧面示意图如图2所示,前轮的直径为 , 拖盘与后轮相切于点N,手柄 . 侧面为矩形ABCD的货物置于拖盘上, , . 如图3所示,倾斜一定角度拉车时,货物绕点B旋转,点C落在上,若 , 则的长为 , 同一时刻,点C离地面高度 , 则点A离地面高度为 .

三、解答题(共8题,共72分)
-
17. 如图1,在中,为的直径,点为上一点,为的平分线交于点 , 连接交于点 .
 (1)、求的度数;(2)、如图2,过点作的切线交延长线于点 , 过点作交于点 . 若 , 求的长.18. 如图,以为直径的上有两点、 , , 过点作直线交的延长线于点 , 交的延长线于点 , 过作平分交于点 , 交于点 .
(1)、求的度数;(2)、如图2,过点作的切线交延长线于点 , 过点作交于点 . 若 , 求的长.18. 如图,以为直径的上有两点、 , , 过点作直线交的延长线于点 , 交的延长线于点 , 过作平分交于点 , 交于点 . (1)、求证:是的切线;(2)、求证:;(3)、如果是的中点,且 , 求的长.19. 如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)、求证:是的切线;(2)、求证:;(3)、如果是的中点,且 , 求的长.19. 如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. (1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若tan∠ADC= ,AC=2,求⊙O的半径;(3)、如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.20. 在平面直角坐标系xOy中,点P不在坐标轴上,点P关于x轴的对称点为P1 , 点P关于y轴的对称点为P2 , 称△P1PP2为点P的“关联三角形”.
(1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若tan∠ADC= ,AC=2,求⊙O的半径;(3)、如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.20. 在平面直角坐标系xOy中,点P不在坐标轴上,点P关于x轴的对称点为P1 , 点P关于y轴的对称点为P2 , 称△P1PP2为点P的“关联三角形”. (1)、已知点A(1,2),求点A的“关联三角形”的面积;(2)、如图,已知点B(m,n),⊙T的圆心为T(2,2),半径为2.若点B的“关联三角形”与⊙T有公共点,直接写出m的取值范围;(3)、已知⊙O的半径为r,OP=2r,若点P的“关联三角形”与⊙O有四个公共点,直接写出∠PP1P2的取值范围.21. 如图,菱形 中,对角线 、 相交于点 , , ,动点 从点 出发,沿线段 以 的速度向点 运动,同时动点 从点 出发,沿线段 以 支向点 运动,当其中一个动点停止时另一个动点也随之停止,设运动时间为 (单位: )( ),以点 为圆心, 长为半径的⊙M与射线 、线段 分别交于点 、 ,连接 .
(1)、已知点A(1,2),求点A的“关联三角形”的面积;(2)、如图,已知点B(m,n),⊙T的圆心为T(2,2),半径为2.若点B的“关联三角形”与⊙T有公共点,直接写出m的取值范围;(3)、已知⊙O的半径为r,OP=2r,若点P的“关联三角形”与⊙O有四个公共点,直接写出∠PP1P2的取值范围.21. 如图,菱形 中,对角线 、 相交于点 , , ,动点 从点 出发,沿线段 以 的速度向点 运动,同时动点 从点 出发,沿线段 以 支向点 运动,当其中一个动点停止时另一个动点也随之停止,设运动时间为 (单位: )( ),以点 为圆心, 长为半径的⊙M与射线 、线段 分别交于点 、 ,连接 . (1)、求 的长(用含有 的代数式表示),并求出 的取值范围;(2)、当 为何值时,线段 与⊙M相切?(3)、若⊙M与线段 只有一个公共点,求 的取值范围.22. 如图,在中, , 以为直径的与交于点D,点是的中点,连接 , .
(1)、求 的长(用含有 的代数式表示),并求出 的取值范围;(2)、当 为何值时,线段 与⊙M相切?(3)、若⊙M与线段 只有一个公共点,求 的取值范围.22. 如图,在中, , 以为直径的与交于点D,点是的中点,连接 , .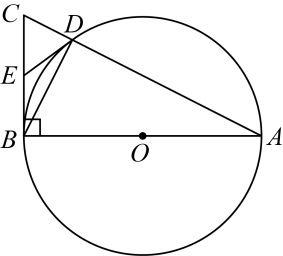 (1)、求证:是的切线;(2)、若 , , 求的长;(3)、在(2)的条件下,点P是上一动点,求的最大值.23. 旋转的图形带来结论的奥秘.已知 , 将绕点逆时针旋转得到.
(1)、求证:是的切线;(2)、若 , , 求的长;(3)、在(2)的条件下,点P是上一动点,求的最大值.23. 旋转的图形带来结论的奥秘.已知 , 将绕点逆时针旋转得到.初步探索
素材1:

如图①,连接对应点 , , 则.
素材2:

如图②,以为圆心,边上的高为半径作 , 则与相切.
问题解决
(1)(ⅰ)请证明素材1所发现的结论.
(ⅱ)如图2,过点作 , 垂足为.证明途径可以用下面的框图表示,请填写其中的空格.

深入研究
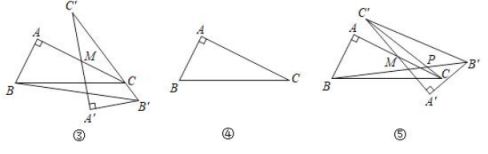
(2)在满足 , , 是的中点,绕点逆时针旋转得.
(ⅰ)如图③,当边恰好经过点时,连接 , 则的长为▲ .
(ⅱ)若一时边所在直线恰好经过点 , 于图④中利用无刻度的直尺和圆规作出直线.(只保留作图痕迹)
(3)在(2)的条件下,如图⑤,在旋转过程中,直线 , 交于点 , 求的最大值为▲ .
24. 【问题情景】含角的直角三角板中 . 将其绕直角顶点C顺时针旋转α角 , 得到 , 边与边AB交于点D.
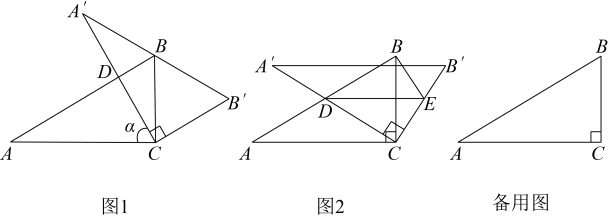 (1)、如图1,若边经过点B,则α的度数为°;(2)、【探究发现】
(1)、如图1,若边经过点B,则α的度数为°;(2)、【探究发现】如图2是旋转过程的一个位置,过点D作交边于点E,连接 , 小明发现在三角板旋转的过程中,度数是定值,求的度数;
(3)、【拓展延伸】在(2)的条件下,设 , 的面积为S,当时,
①求的长;
②以点E为圆心,为半径作 , 并判断此时直线与的位置关系.