(基础卷)2.1 直线与圆的位置关系-2023-2024年浙教版数学九年级下册同步测试
试卷更新日期:2023-09-10 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 的半径为5,圆心O到直线l的距离为3,则直线l与 的位置关系是A、相交 B、相切 C、相离 D、无法确定2. 已知的直径为12,点O到直线l上一点的距离为 , 则直线l与的位置关系( )A、相交 B、相切 C、相离 D、不确定3. 若 , , 则以点O为圆心,为半径的圆与直线的位置关系是( )A、相交 B、相切 C、相离 D、不能确定4. 已知⊙O的半径等于5,圆心O到直线l的距离为6,那么直线l与⊙O的公共点的个数是( )A、0 B、1 C、2 D、无法确定5. 面直角坐标系中,以点为圆心,为半径的圆一定与( )A、轴相交 B、轴相交 C、轴相切 D、轴相切6. 如图,若的半径为5,圆心O到一条直线的距离为2,则这条直线可能是( )
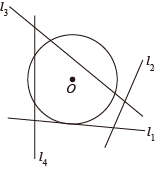 A、 B、 C、 D、7. 如图,AB是⊙O的直径,BC是⊙O的切线.若∠BAC=37°,则∠ACB的大小为( )
A、 B、 C、 D、7. 如图,AB是⊙O的直径,BC是⊙O的切线.若∠BAC=37°,则∠ACB的大小为( ) A、37° B、47° C、53° D、63°8. 如图所示,AE切⊙D于点E,AC=CD=DB=10,则线段AE的长为( )
A、37° B、47° C、53° D、63°8. 如图所示,AE切⊙D于点E,AC=CD=DB=10,则线段AE的长为( )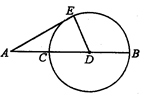 A、10 B、15 C、10 D、209. 如图,以点P为圆心作圆,所得的圆与直线l相切的是( )
A、10 B、15 C、10 D、209. 如图,以点P为圆心作圆,所得的圆与直线l相切的是( ) A、以PA为半径的圆 B、以PB为半径的 C、以PC为半径的圆 D、以PD为半径的圆10. 如图,PA、PB是⊙O的切线,A、B为切点,若∠AOB= 128 ,则∠P的度数为( )
A、以PA为半径的圆 B、以PB为半径的 C、以PC为半径的圆 D、以PD为半径的圆10. 如图,PA、PB是⊙O的切线,A、B为切点,若∠AOB= 128 ,则∠P的度数为( )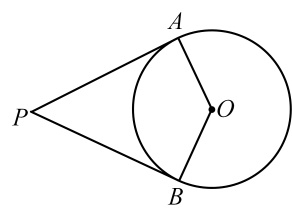 A、32° B、52° C、64° D、72°
A、32° B、52° C、64° D、72°二、填空题(每空4分,共24分)
-
11. 已知的半径 , 圆心O到直线l的距离 , 则直线l与的位置关系是 .12. 初中生小明日常骑自行车上下学,某日小明沿地面一条直线骑行,自行车轮胎与这条直线的位置关系是 . (填“相离”、“相交”或“相切”)
 13. ⊙O的半径为5cm,点O到直线AB的距离为d,当d=时,AB与⊙O相切.14. 已知⊙O的半径为10,直线AB与⊙O相切,则圆心O到直线AB的距离为 .15. 如图,点A、B、D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,直线BC与⊙O的位置关系为 .
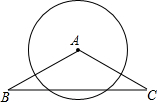
13. ⊙O的半径为5cm,点O到直线AB的距离为d,当d=时,AB与⊙O相切.14. 已知⊙O的半径为10,直线AB与⊙O相切,则圆心O到直线AB的距离为 .15. 如图,点A、B、D在⊙O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,直线BC与⊙O的位置关系为 . 16. 如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为 .
16. 如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为 .
三、解答题(共4题,共24分)
-
17. 如图,在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由.
 18. 设⊙O的圆心O到直线的距离为d,半径为r,且直线与⊙O相切.d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,求m的值.19. 如图,在两个同心圆O中,、都是大圆的弦,且 , 与小圆相切于点D,则与小圆相切吗?请说明理由.
18. 设⊙O的圆心O到直线的距离为d,半径为r,且直线与⊙O相切.d,r是一元二次方程(m+9)x2-(m+6)x+1=0的两根,求m的值.19. 如图,在两个同心圆O中,、都是大圆的弦,且 , 与小圆相切于点D,则与小圆相切吗?请说明理由.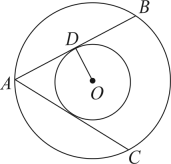 20. 如图,线段AB经过圆心O,交⊙O于点A、C,AD为⊙O的弦,连结BD,∠BAD=∠B=30°,直线BD是⊙O的切线吗?如果是,请给出证明.
20. 如图,线段AB经过圆心O,交⊙O于点A、C,AD为⊙O的弦,连结BD,∠BAD=∠B=30°,直线BD是⊙O的切线吗?如果是,请给出证明.
四、综合题(共4题,共42分)
-
21. 如图,在中, , 的角平分线交于点D,点O在上,以点O为圆心,为半径的圆恰好经过点D,分别交、于点E,F.
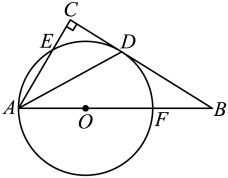 (1)、试判断直线与⊙O的位置关系,并说明理由;(2)、若 , , 求⊙O的半径.22. 在平面直角坐标系中,以坐标原点为圆心的⊙O半径为3.(1)、试判断点A(3,3)与⊙O的位置关系,并加以说明.(2)、若直线y=x+b与⊙O相交,求b的取值范围.(3)、若直线y=x+3与⊙O相交于点A,B.点P是x轴正半轴上的一个动点,以A,B,P三点为顶点的三角形是等腰三角形,求点P的坐标.
(1)、试判断直线与⊙O的位置关系,并说明理由;(2)、若 , , 求⊙O的半径.22. 在平面直角坐标系中,以坐标原点为圆心的⊙O半径为3.(1)、试判断点A(3,3)与⊙O的位置关系,并加以说明.(2)、若直线y=x+b与⊙O相交,求b的取值范围.(3)、若直线y=x+3与⊙O相交于点A,B.点P是x轴正半轴上的一个动点,以A,B,P三点为顶点的三角形是等腰三角形,求点P的坐标.

