(B卷)第一章 解直角三角形-浙教版数学九年级下册单元测试
试卷更新日期:2023-09-10 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 在Rt△ABC中,∠C=90°,下列等式不一定成立的( )A、a=csinA B、a=btanA C、 D、sin2A+sin2B=12. 如图,在6×6的正方形网格中,每个小正方形的边长都是1,点A,B,C均在网格交点上,⊙O是△ABC的外接圆,则sin∠BAC的值为( )
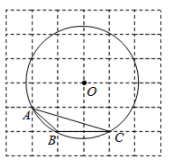 A、 B、 C、 D、3. 如图,⊙O是以坐标原点O为圆心, 为半径的圆,点P的坐标为(2,2),弦AB经过点P,则图中阴影部分面积的最小值为( )
A、 B、 C、 D、3. 如图,⊙O是以坐标原点O为圆心, 为半径的圆,点P的坐标为(2,2),弦AB经过点P,则图中阴影部分面积的最小值为( ) A、8π B、 C、8π﹣16 D、4. 用计算器求sin24°37′18″的值,以下按键顺序正确的是( )A、
A、8π B、 C、8π﹣16 D、4. 用计算器求sin24°37′18″的值,以下按键顺序正确的是( )A、 B、
B、 C、
C、 D、
D、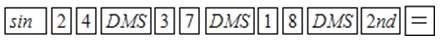 5. 如图,AC,BC是两个半圆的直径,∠ACP=30°,若AB=2a,则 PQ的值为( )
5. 如图,AC,BC是两个半圆的直径,∠ACP=30°,若AB=2a,则 PQ的值为( )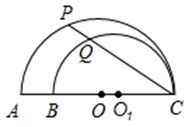 A、a B、1.5a C、 D、6. 某路灯示意图如图所示,它是轴对称图形.若 , , 与地面垂直且 , 则灯顶A到地面的高度为( )m
A、a B、1.5a C、 D、6. 某路灯示意图如图所示,它是轴对称图形.若 , , 与地面垂直且 , 则灯顶A到地面的高度为( )m A、 B、 C、 D、7. 消防云梯如图所示,AB⊥BC于B,当C点刚好在A点的正上方时,DF的长是.( )
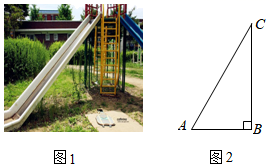
A、 B、 C、 D、7. 消防云梯如图所示,AB⊥BC于B,当C点刚好在A点的正上方时,DF的长是.( ) A、 B、 C、 D、8. 图1是某公园的一个滑梯,图2是其示意图.滑梯的高BC为2m,坡角∠A为60°,由于滑梯坡角过大存在安全隐忠,公园管理局决定对滑梯进行整改,要在高度不变的前提下,通过加长滑梯的水平距离AB,使得坡角∠A满足30°≤∠A≤45°,则AB加长的距离可以是( )
A、 B、 C、 D、8. 图1是某公园的一个滑梯,图2是其示意图.滑梯的高BC为2m,坡角∠A为60°,由于滑梯坡角过大存在安全隐忠,公园管理局决定对滑梯进行整改,要在高度不变的前提下,通过加长滑梯的水平距离AB,使得坡角∠A满足30°≤∠A≤45°,则AB加长的距离可以是( )(参考数据: ≈1.414, ≈1.732)
 A、0.8m B、1.6m C、2.4m D、3.2m9. 如图1,以的各边为边向外作等边三角形,编号分别为①,②,③.如图2,将①,②叠放在③中,若四边形与的面积之比是 , 则的值是( )
A、0.8m B、1.6m C、2.4m D、3.2m9. 如图1,以的各边为边向外作等边三角形,编号分别为①,②,③.如图2,将①,②叠放在③中,若四边形与的面积之比是 , 则的值是( )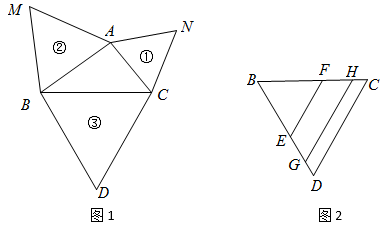 A、 B、 C、 D、10. 如图,菱形ABCD中,对角线AC,BD相交于点O,AC=12cm,BD=16cm,动点N从点D出发,沿线段DB以2cm/s的速度向点B运动,同时动点M从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随之停止,设运动时间为t(s)(t>0),以点M为圆心,MB长为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.若⊙M与线段EN只有一个公共点,则t的取值范围为( )
A、 B、 C、 D、10. 如图,菱形ABCD中,对角线AC,BD相交于点O,AC=12cm,BD=16cm,动点N从点D出发,沿线段DB以2cm/s的速度向点B运动,同时动点M从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随之停止,设运动时间为t(s)(t>0),以点M为圆心,MB长为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.若⊙M与线段EN只有一个公共点,则t的取值范围为( )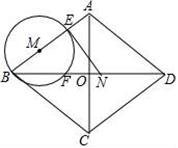 A、0<t≤ 或 <t<6 B、0<t≤ 或 <t<8 C、0<t≤ 或 <t<6 D、0<t≤ 或 <t<8
A、0<t≤ 或 <t<6 B、0<t≤ 或 <t<8 C、0<t≤ 或 <t<6 D、0<t≤ 或 <t<8二、填空题(每题3分,共18分)
-
11. 如图1是一款手机支架,水平放置时,它的侧面示意图如图2所示,其中线段 , , , 是支撑杆且 , , 可以自由调节大小已知 , , 当时,点恰好在点的正上方,则线段 ;如图3,保持不变,旋转至 , 使点 , , 恰好在一条直线上,则此时点到点上升的竖直高度为 .
 12. 如图,半径为6cm的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连结AE,BF,则图中两个阴影部分的面积为cm2
12. 如图,半径为6cm的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连结AE,BF,则图中两个阴影部分的面积为cm2 13. 如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是y= ,则图象经过点D的反比例函数的解析式是 .
13. 如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是y= ,则图象经过点D的反比例函数的解析式是 .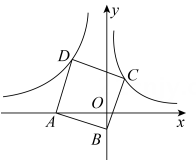 14. 如图是某风车示意图,其相同的四个叶片均匀分布,水平地而上的点M在旋转中心O的正下方。某一时刻,太阳光线恰好垂直照射叶片 OA、OB ,此时各叶片影子在点M右侧成线段 CD ,测得MC=8.5m,CD=13m,垂直于地面的木棒 EF 与影子 FG 的比为2∶3,则点O,M之间的距离等于米.转动时,叶片外端离地面的最大高度等于米.
14. 如图是某风车示意图,其相同的四个叶片均匀分布,水平地而上的点M在旋转中心O的正下方。某一时刻,太阳光线恰好垂直照射叶片 OA、OB ,此时各叶片影子在点M右侧成线段 CD ,测得MC=8.5m,CD=13m,垂直于地面的木棒 EF 与影子 FG 的比为2∶3,则点O,M之间的距离等于米.转动时,叶片外端离地面的最大高度等于米. 15. 如图,为了配合疫情工作,浦江某学校门口安装了体温监测仪器,体温检测有效识别区域AB长为6米,当身高为1.5米的学生进入识别区域时,在点B处测得摄像头M的仰角为 , 当学生刚好离开识别区域时,在点A处测得摄像头M的仰角为 , 则学校大门ME的高是米.
15. 如图,为了配合疫情工作,浦江某学校门口安装了体温监测仪器,体温检测有效识别区域AB长为6米,当身高为1.5米的学生进入识别区域时,在点B处测得摄像头M的仰角为 , 当学生刚好离开识别区域时,在点A处测得摄像头M的仰角为 , 则学校大门ME的高是米.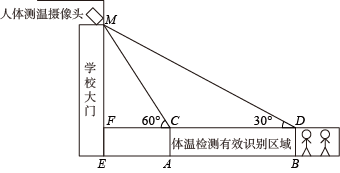 16. 如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为米(精确到1米,参考数据 ≈1.414, ≈1.732)。
16. 如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为米(精确到1米,参考数据 ≈1.414, ≈1.732)。
三、解答题(共9题,共72分)
-
17. 设a、b、c是直角三角形的三边,c为斜边,n为正整数,试判断an+bn与cn的关系,并证明你的结论.18. 如图,在矩形 中, 于点 ,交 边于点 . 平分 交 于点 ,并经过 边的中点 .
 (1)、求证: .(2)、求 的值.(3)、若 ,试在 上找一点 (不与 , 重合),使直线 经过四边形 一边的中点,求所有满足条件的 的值.19. 图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,摄像头高度 , 识别的最远水平距离。
(1)、求证: .(2)、求 的值.(3)、若 ,试在 上找一点 (不与 , 重合),使直线 经过四边形 一边的中点,求所有满足条件的 的值.19. 图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,摄像头高度 , 识别的最远水平距离。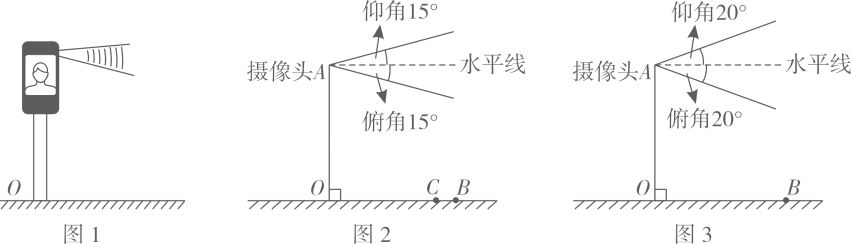 (1)、身高的小杜,头部高度为 , 他站在离摄像头水平距离的点C处,请问小杜最少需要下蹲多少厘米才能被识别。(2)、身高的小若,头部高度为 , 踮起脚尖可以增高 , 但仍无法被识别.社区及时将摄像头的仰角、俯角都调整为(如图3),此时小若能被识别吗?请计算说明。
(1)、身高的小杜,头部高度为 , 他站在离摄像头水平距离的点C处,请问小杜最少需要下蹲多少厘米才能被识别。(2)、身高的小若,头部高度为 , 踮起脚尖可以增高 , 但仍无法被识别.社区及时将摄像头的仰角、俯角都调整为(如图3),此时小若能被识别吗?请计算说明。(精确到 , 参考数据)
20. 如图 (1)、【问题发现】如图1,P是半径为2的⊙O上一点,直线m是⊙O外一直线,圆心O到直线m的距离为3,PQ⊥m于点Q,则PQ的最大值为;(2)、【问题探究】如图2,将两个含有30°角的直角三角板的60°角的顶点重合(其中∠A==30°,∠C=∠C'=90°),绕点B旋转 , 当旋转至CC′=4时,求的长;(3)、【问题解决】如图3,点O为等腰RtABC的斜边AB的中点,AC=BC=5 , OE=2,连接BE,作RtBEF,其中∠BEF=90°,tan∠EBF= , 连接AF,求四边形ACBF的面积的最大值.21. 足球射门时,在不考虑其他因素的条件下,射点到球门AB的张角越大,射门越好.当张角达到最大值时,我们称该射点为最佳射门点.通过研究发现,如图1所示,运动员带球在直线CD上行进时,当存在一点Q,使得(此时也有)时,恰好能使球门AB的张角达到最大值,故可以称点Q为直线CD上的最佳射门点.
(1)、【问题发现】如图1,P是半径为2的⊙O上一点,直线m是⊙O外一直线,圆心O到直线m的距离为3,PQ⊥m于点Q,则PQ的最大值为;(2)、【问题探究】如图2,将两个含有30°角的直角三角板的60°角的顶点重合(其中∠A==30°,∠C=∠C'=90°),绕点B旋转 , 当旋转至CC′=4时,求的长;(3)、【问题解决】如图3,点O为等腰RtABC的斜边AB的中点,AC=BC=5 , OE=2,连接BE,作RtBEF,其中∠BEF=90°,tan∠EBF= , 连接AF,求四边形ACBF的面积的最大值.21. 足球射门时,在不考虑其他因素的条件下,射点到球门AB的张角越大,射门越好.当张角达到最大值时,我们称该射点为最佳射门点.通过研究发现,如图1所示,运动员带球在直线CD上行进时,当存在一点Q,使得(此时也有)时,恰好能使球门AB的张角达到最大值,故可以称点Q为直线CD上的最佳射门点. (1)、如图2所示,AB为球门,当运动员带球沿CD行进时, , , 为其中的三个射门点,则在这三个射门点中,最佳射门点为点;(2)、如图3所示,是一个矩形形状的足球场,AB为球门,于点D, , .某球员沿CD向球门AB进攻,设最佳射门点为点Q.
(1)、如图2所示,AB为球门,当运动员带球沿CD行进时, , , 为其中的三个射门点,则在这三个射门点中,最佳射门点为点;(2)、如图3所示,是一个矩形形状的足球场,AB为球门,于点D, , .某球员沿CD向球门AB进攻,设最佳射门点为点Q.①用含a的代数式表示DQ的长度并求出的值;
②已知对方守门员伸开双臂后,可成功防守的范围为 , 若此时守门员站在张角内,双臂张开MN垂直于AQ进行防守,求MN中点与AB的距离至少为多少时才能确保防守成功.(结果用含a的代数式表示)
22. 如图 (1)、【基础巩固】如图1,和都是等边三形,点B、D、E在同条直线上,与交于点F.求证:.(2)、【尝试应用】
(1)、【基础巩固】如图1,和都是等边三形,点B、D、E在同条直线上,与交于点F.求证:.(2)、【尝试应用】
如图2,在(1)的条件下,若 , 求的长度.(3)、【拓展提高】
如图3,在平行四边形ABCD中, , , , 求的值.23. 【证明体验】(1)、如图1,正方形中, , 分别是边和对角线上的点, , . 求证: .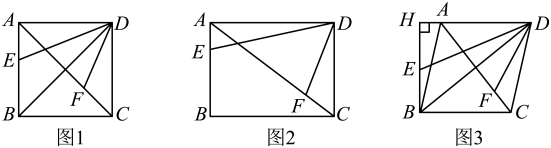 (2)、【思考探究】
(2)、【思考探究】
如图2,矩形中, , , , 分别是边和对角线上的点, , , 求的长.(3)、【拓展延伸】
如图3,菱形中, , 对角线 , 交的延长线于点 , , 分别是线段和上的点, , , 求BE的长.24. 如图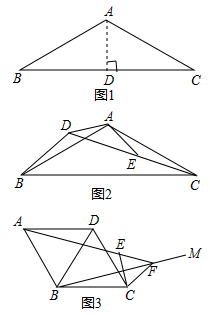 (1)、【问题背景】如图1,等腰△ABC,AB=AC,∠BAC=120°则 = .(2)、【迁移应用】如图2,△ABC和△ABE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同-条直线上,连结BD.求线段AD,BD,CD之间的数量关系式;(3)、【拓展延伸】如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连结AE并延长交BM于点F,连结CE, CF.若AE=4,CE=1.求BF的长.25. 如图,在四边形中, , 点分别在边和边上,.点在上从点匀速运动到点时,点恰好从上某一点匀速运动到点 , 记 , 已知.
(1)、【问题背景】如图1,等腰△ABC,AB=AC,∠BAC=120°则 = .(2)、【迁移应用】如图2,△ABC和△ABE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同-条直线上,连结BD.求线段AD,BD,CD之间的数量关系式;(3)、【拓展延伸】如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连结AE并延长交BM于点F,连结CE, CF.若AE=4,CE=1.求BF的长.25. 如图,在四边形中, , 点分别在边和边上,.点在上从点匀速运动到点时,点恰好从上某一点匀速运动到点 , 记 , 已知.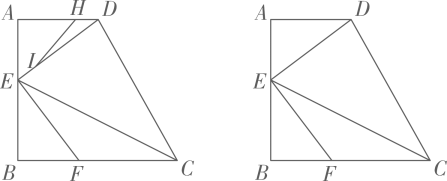 (1)、求证:.(2)、求的长与的值.(3)、连结.
(1)、求证:.(2)、求的长与的值.(3)、连结.①当直线与一边垂直时,求所有满足条件的的值.
②线段绕点顺时针旋转得到线段 , 当点恰好落在上时,求和的面积比.