(A卷)第一章 解直角三角形-浙教版数学九年级下册单元测试
试卷更新日期:2023-09-10 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 在中, , , , 则的长为( )A、 B、 C、 D、2. 计算的值是( )A、 B、 C、 D、3. 在RtΔABC中,若∠C=90°,cosA= ,则sinA的值为( )A、 B、 C、 D、4. 已知是锐角, , 则的值为( )A、30° B、60° C、45° D、无法确定5. 已知 ,则 的度数所属范围是( )A、
 B、
C、
D、
6. 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
B、
C、
D、
6. 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )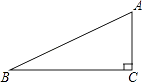 A、
A、 B、
B、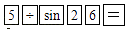 C、
C、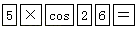 D、
D、 7. 如图,一把梯子靠在垂直水平地面的墙上,梯子底端A到墙面的距离为6米,若梯子与地面的夹角为α,则梯子的长为( )
7. 如图,一把梯子靠在垂直水平地面的墙上,梯子底端A到墙面的距离为6米,若梯子与地面的夹角为α,则梯子的长为( ) A、米 B、米 C、米 D、米8. 如图,圆规两脚张开的角度为α, , 则两脚张开的距离为( )
A、米 B、米 C、米 D、米8. 如图,圆规两脚张开的角度为α, , 则两脚张开的距离为( ) A、 B、 C、 D、9. 如图,某超市电梯的截面图中,的长为15米,与的夹角为 , 则高是( )
A、 B、 C、 D、9. 如图,某超市电梯的截面图中,的长为15米,与的夹角为 , 则高是( )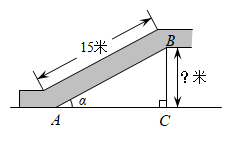 A、米 B、米 C、米 D、米10. 如图,我市在建高铁的某段路基横断面为梯形 , . 长6米,坡度为 , 的坡度为 , 则长为( ) 米
A、米 B、米 C、米 D、米10. 如图,我市在建高铁的某段路基横断面为梯形 , . 长6米,坡度为 , 的坡度为 , 则长为( ) 米 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
11. 如图,在中, , 点D为边的中点,连接 , 若 , 则的值是.
 12. 已知为锐角, , 那么度.13. α是锐角,若sinα=cos15°,则α=°.14. 若 为锐角,且 ,则 °.15. 比较大小:sin35°cos45°.16. 某校九年级的一位同学,想利用刚刚学过的三角函数知识测量新教学楼的高度,如图,她在A处测得新教学楼房顶B点的仰角为45°,走6米到C处再测得B点的仰角为55°,已知O、A、C在同一条直线上,则新教学楼的高度OB是米.(结果根据“四舍五入”法保留小数点后两位)(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
12. 已知为锐角, , 那么度.13. α是锐角,若sinα=cos15°,则α=°.14. 若 为锐角,且 ,则 °.15. 比较大小:sin35°cos45°.16. 某校九年级的一位同学,想利用刚刚学过的三角函数知识测量新教学楼的高度,如图,她在A处测得新教学楼房顶B点的仰角为45°,走6米到C处再测得B点的仰角为55°,已知O、A、C在同一条直线上,则新教学楼的高度OB是米.(结果根据“四舍五入”法保留小数点后两位)(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)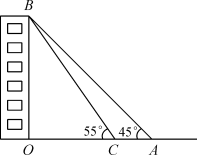
三、解答题(共9题,共72分)
-
17. 计算:.18. 先化简,再求值: , 其中.19. 如图,已知中, , , , 边的垂直平分线分别交、于点D、E.求线段的长.
 20. 如图所示,在△ABC中, , D为上一点,若 , , 求和的值.
20. 如图所示,在△ABC中, , D为上一点,若 , , 求和的值. 21. 如图,在中, , 平分交边于点D,于点E,若 , , 求的长.
21. 如图,在中, , 平分交边于点D,于点E,若 , , 求的长. 22. 已知如图,A,B,C,D四点的坐标分别是(3,0),(0,4),(12,0),(0,9),探索∠OBA和∠OCD的大小关系,并说明理由.
22. 已知如图,A,B,C,D四点的坐标分别是(3,0),(0,4),(12,0),(0,9),探索∠OBA和∠OCD的大小关系,并说明理由. 23. 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对().如图,在中, , 顶角A的正对记作 , 这时.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题:
23. 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对().如图,在中, , 顶角A的正对记作 , 这时.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题: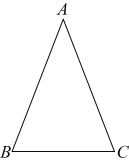 (1)、 的值为( ).A、 B、1 C、 D、2(2)、对于 , 的正对值的取值范围是.(3)、已知 , 其中α为锐角,试求的值.24. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线.为了测量房屋的高度,在地面上点测得屋顶的仰角为 , 此时地面上点、屋檐上点、屋顶上点三点恰好共线,继续向房屋方向走到达点时,又测得屋檐点的仰角为 , 房屋的顶层横梁 , , 交于点(点 , , 在同一水平线上).(参考数据: , , , )
(1)、 的值为( ).A、 B、1 C、 D、2(2)、对于 , 的正对值的取值范围是.(3)、已知 , 其中α为锐角,试求的值.24. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线.为了测量房屋的高度,在地面上点测得屋顶的仰角为 , 此时地面上点、屋檐上点、屋顶上点三点恰好共线,继续向房屋方向走到达点时,又测得屋檐点的仰角为 , 房屋的顶层横梁 , , 交于点(点 , , 在同一水平线上).(参考数据: , , , ) (1)、求屋顶到横梁的距离;(2)、求房屋的高(结果精确到1m).25. 如图,笔直的海岸线l上有A、B两个观测站,A在B的正东方向.有一艘渔船在点P处,从A处测得渔船在北偏西的方向,从B处测得渔船在其东北方向,且测得B、P两点之间的距离为20海里.
(1)、求屋顶到横梁的距离;(2)、求房屋的高(结果精确到1m).25. 如图,笔直的海岸线l上有A、B两个观测站,A在B的正东方向.有一艘渔船在点P处,从A处测得渔船在北偏西的方向,从B处测得渔船在其东北方向,且测得B、P两点之间的距离为20海里. (1)、求观测站A、B之间的距离(结果保留根号);(2)、渔船从点P处沿射线的方向航行一段时间后,到点C处等待补给,此时,从B测得渔船在北偏西的方向.在渔船到达C处的同时,一艘补给船从点B出发,以每小时20海里的速度前往C处,请问补给船能否在83分钟之内到达C处?(参考数据:)
(1)、求观测站A、B之间的距离(结果保留根号);(2)、渔船从点P处沿射线的方向航行一段时间后,到点C处等待补给,此时,从B测得渔船在北偏西的方向.在渔船到达C处的同时,一艘补给船从点B出发,以每小时20海里的速度前往C处,请问补给船能否在83分钟之内到达C处?(参考数据:)