(提升卷)1.3解直角三角形-2023-2024年浙教版数学九年级下册同步测试
试卷更新日期:2023-09-10 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,若△ABC底边BC上的高为h1 , △DEF底边EF上的高为h2 , 则h1与h2的大小关系是( )
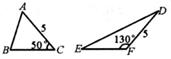 A、h1=h2 B、h1<h2 C、h1>h2 D、以上都有可能2. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1,∠AOB=α,则 OC2的值为( )
A、h1=h2 B、h1<h2 C、h1>h2 D、以上都有可能2. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1,∠AOB=α,则 OC2的值为( )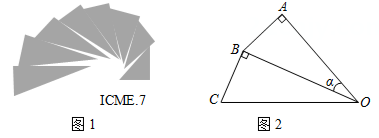 A、 B、 C、 D、3. 如图是一段索道的示意图. 若 米, , 则洗车从 点到 点上升的高度 的长为( )
A、 B、 C、 D、3. 如图是一段索道的示意图. 若 米, , 则洗车从 点到 点上升的高度 的长为( ) A、 米 B、 米 C、 米 D、 米4. 如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作交于点C,若OA=2,则阴影部分的面积为( )
A、 米 B、 米 C、 米 D、 米4. 如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作交于点C,若OA=2,则阴影部分的面积为( ) A、 B、 C、 D、5. 如图,在Rt中,.以点为圆心,CB长为半径的圆交AB于点 , 则AD的长是( )
A、 B、 C、 D、5. 如图,在Rt中,.以点为圆心,CB长为半径的圆交AB于点 , 则AD的长是( ) A、1 B、 C、 D、26. 我国伟大的数学家刘徽于公元263年攥《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形ABCDEF是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结AG,CF,AG交CF于点P,AP=2 , 则 =( )
A、1 B、 C、 D、26. 我国伟大的数学家刘徽于公元263年攥《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形ABCDEF是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结AG,CF,AG交CF于点P,AP=2 , 则 =( )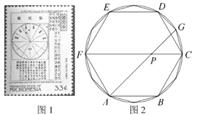 A、2 B、 C、 D、7. 图1是一种落地晾衣架,晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,和分别是两根不同长度的支撑杆,其中两支脚 , 展开角 , 晾衣臂 , 则支樟杆的端点离地面的高度为( )
A、2 B、 C、 D、7. 图1是一种落地晾衣架,晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,和分别是两根不同长度的支撑杆,其中两支脚 , 展开角 , 晾衣臂 , 则支樟杆的端点离地面的高度为( )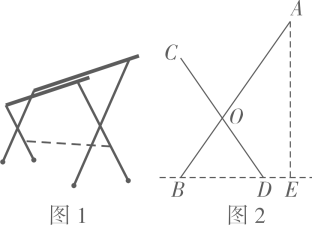 A、 B、 C、 D、8. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )
A、 B、 C、 D、8. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )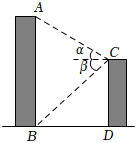 A、 B、 C、 D、9. 如图,点O为小亮家的位置,他家门前有一条东西走向的公路,水塔A位于他家北偏东60°的500米处,那么水塔所在的位置到公路的距离是( )
A、 B、 C、 D、9. 如图,点O为小亮家的位置,他家门前有一条东西走向的公路,水塔A位于他家北偏东60°的500米处,那么水塔所在的位置到公路的距离是( ) A、250米 B、250 C、150 D、25010. 图1是一块矩形材料 ,被分割成三块, , ,将三块材料无缝隙不重叠地拼成图2的形状,此时图2恰好是轴对称图形,则
A、250米 B、250 C、150 D、25010. 图1是一块矩形材料 ,被分割成三块, , ,将三块材料无缝隙不重叠地拼成图2的形状,此时图2恰好是轴对称图形,则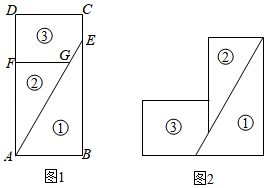 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空4分,共24分)
-
11. 小明沿着坡比为1:2的山坡向上走了10m,则他升高了cm。12. 如图,小明家附近有一观光塔CD,他发现当光线角度变化时,观光塔的影子在地面上的长度也发生变化.经测量发现,当小明站在点A处时,塔顶D的仰角为37°,他往前再走5米到达点B(点A,B,C在同一直线上),塔顶D的仰角为53°,则观光塔CD的高度约为 .(精确到0.1米,参考数值:tan37°≈ ,tan53°≈ )
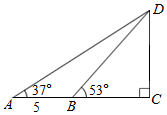 13. 如图,A位于学校主教学楼P南偏东45°方向,且距离教学楼60米,小明同学从这里出发沿着正北方向走了一段时间后,到达位于主教学楼北偏东30°方向的综合楼B处,此时小明同学一共走的距离为米.
13. 如图,A位于学校主教学楼P南偏东45°方向,且距离教学楼60米,小明同学从这里出发沿着正北方向走了一段时间后,到达位于主教学楼北偏东30°方向的综合楼B处,此时小明同学一共走的距离为米. 14. 如图,以C为公共顶点的和中, , , 且点D在线段上,则 , 若 , 则.
14. 如图,以C为公共顶点的和中, , , 且点D在线段上,则 , 若 , 则.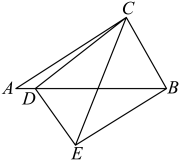 15. 如图,在Rt△ABC中,∠ACB=90°,AC<BC,CD平分∠ACB交AB于点D,以DB为直径作⊙O,分别交CD,BC于点E,F,连结BE,EF.则∠EBF=度;若DE=DC, BC=8,则EF的长为
15. 如图,在Rt△ABC中,∠ACB=90°,AC<BC,CD平分∠ACB交AB于点D,以DB为直径作⊙O,分别交CD,BC于点E,F,连结BE,EF.则∠EBF=度;若DE=DC, BC=8,则EF的长为 16. 图1是一台实物投影仪,图2是它的示意图,折线表示固定支架,垂直水平桌面于点 , 点为旋转点,可转动,当绕点顺时针旋转时,投影探头始终垂直于水平桌面 , 经测量: , , , .如图 , , .则投影探头的端点到桌面的距离为.如图3,将图2中的向下旋转,当投影探头的端点到桌面的距离为时,则的大小为度.(参考数据: , , , )
16. 图1是一台实物投影仪,图2是它的示意图,折线表示固定支架,垂直水平桌面于点 , 点为旋转点,可转动,当绕点顺时针旋转时,投影探头始终垂直于水平桌面 , 经测量: , , , .如图 , , .则投影探头的端点到桌面的距离为.如图3,将图2中的向下旋转,当投影探头的端点到桌面的距离为时,则的大小为度.(参考数据: , , , )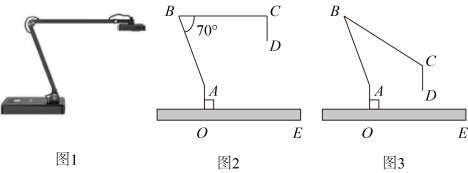
三、解答题(共8题,共66分)
-
17. 如图,在△ABC中,CD是边AB上的中线,∠B是锐角,sinB= , tanA= , AC= .
 (1)、求∠B的度数和AB的长.(2)、求tan∠CDB的值.18. 共享单车为大众出行提供了方便,图1为单车实物图,图2为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知∠ABE=70°,∠EAB=45°,车轮半径为30cm,BE=40cm.小明体验后觉得当坐垫C离地面高度为90cm时骑着比较舒适,求此时CE的长.(结果精确到1cm)(参考数据: , , , )
(1)、求∠B的度数和AB的长.(2)、求tan∠CDB的值.18. 共享单车为大众出行提供了方便,图1为单车实物图,图2为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知∠ABE=70°,∠EAB=45°,车轮半径为30cm,BE=40cm.小明体验后觉得当坐垫C离地面高度为90cm时骑着比较舒适,求此时CE的长.(结果精确到1cm)(参考数据: , , , ) 19. 长嘴壶茶艺表演是一项深受群众喜爱的民俗文化,是我国茶文化的一部分,所用到的长嘴壶更是历史悠久,源远流长.图①是现今使用的某款长嘴壶放置在水平桌面上的照片,图②是其抽象示意图,l是水平桌面,测得壶身AD=BC=3AE=24cm,AB=30cm,CD=22cm,且CD∥AB.壶嘴EF=80cm,∠FED=70°
19. 长嘴壶茶艺表演是一项深受群众喜爱的民俗文化,是我国茶文化的一部分,所用到的长嘴壶更是历史悠久,源远流长.图①是现今使用的某款长嘴壶放置在水平桌面上的照片,图②是其抽象示意图,l是水平桌面,测得壶身AD=BC=3AE=24cm,AB=30cm,CD=22cm,且CD∥AB.壶嘴EF=80cm,∠FED=70° (1)、求FE与水平桌面l的夹角(2)、如图③,若长嘴壶中装有若干茶水,绕点A转动壶身,当恰好倒出茶水时,EF∥l,求此时点F下落的高度.(结果保留一位小数).
(1)、求FE与水平桌面l的夹角(2)、如图③,若长嘴壶中装有若干茶水,绕点A转动壶身,当恰好倒出茶水时,EF∥l,求此时点F下落的高度.(结果保留一位小数).参考数据:sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75.
20. 小华将一张纸对折后做成的纸飞机如图1,纸飞机机尾的横截面是一个轴对称图形,其示意图如图2.已知 , , , , .(结果精确到0.1 , 参考数据: , , , , , )
 (1)、连结 , 求线段的长.(2)、求点A,B之间的距离.21. 如图,有一段斜坡长为10米,坡角 , 为方便残疾人的轮椅车通行,现准备把坡角降为.
(1)、连结 , 求线段的长.(2)、求点A,B之间的距离.21. 如图,有一段斜坡长为10米,坡角 , 为方便残疾人的轮椅车通行,现准备把坡角降为. (1)、求坡高;(2)、求斜坡新起点与原起点的距离精确到0.1米.
(1)、求坡高;(2)、求斜坡新起点与原起点的距离精确到0.1米.参考数据: , ,
22. 如图,在河流两边有甲、乙两座山,现在从甲山处的位置向乙山处拉电线.已知甲山上点到河边的距离米,点到的垂直高度为120米;乙山的坡比为 , 乙山上点到河边的距离米,从处看处的俯角为25°(参考值: , , ) (1)、求乙山处到河边的垂直距离;(2)、求河的宽度.(结果保留整数)23. 如图,在一片海域中有三个岛屿,标记为 , , .经过测量岛屿在岛屿的北偏东 , 岛屿在岛屿的南偏东 , 岛屿在岛屿的南偏东.
(1)、求乙山处到河边的垂直距离;(2)、求河的宽度.(结果保留整数)23. 如图,在一片海域中有三个岛屿,标记为 , , .经过测量岛屿在岛屿的北偏东 , 岛屿在岛屿的南偏东 , 岛屿在岛屿的南偏东. (1)、直接写出的三个内角度数;(2)、小明测得较近两个岛屿 , 求、的长度(最终结果保留根号,不用三角函数表示).24. 定义:若两个三角形中,有两组边对应相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏等三角形.
(1)、直接写出的三个内角度数;(2)、小明测得较近两个岛屿 , 求、的长度(最终结果保留根号,不用三角函数表示).24. 定义:若两个三角形中,有两组边对应相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏等三角形. (1)、如图1,点C是的中点,∠DAB是所对的圆周角,AD>AB,连结AC、DC、CB,试说明△ACB与△ACD是偏等三角形.(2)、如图2,△ABC与△DEF是偏等三角形,其中∠A=∠D,AC=DF,BC=EF,则∠B+∠E=.请填写结论,并说明理由.(3)、如图3,△ABC内接于⊙O,AC=4,∠A=30°,∠B=105°,若点D在⊙O上,且△ADC与△ABC是偏等三角形,AD>CD,求AD的值.
(1)、如图1,点C是的中点,∠DAB是所对的圆周角,AD>AB,连结AC、DC、CB,试说明△ACB与△ACD是偏等三角形.(2)、如图2,△ABC与△DEF是偏等三角形,其中∠A=∠D,AC=DF,BC=EF,则∠B+∠E=.请填写结论,并说明理由.(3)、如图3,△ABC内接于⊙O,AC=4,∠A=30°,∠B=105°,若点D在⊙O上,且△ADC与△ABC是偏等三角形,AD>CD,求AD的值.