(培优卷)1.3解直角三角形-2023-2024年浙教版数学九年级下册同步测试
试卷更新日期:2023-09-10 类型:同步测试
一、选择题(每题2分,共20分)
-
1. 如图,在纸片 中, ,折叠纸片,使点 落在 的中点 处,折痕为 ,则 的面积为( )
 A、 B、 C、 D、2. 如图,以O为圆心的圆与反比例函数 的图象交于 两点,已知点B的坐标为 ,则 的长度为( )
A、 B、 C、 D、2. 如图,以O为圆心的圆与反比例函数 的图象交于 两点,已知点B的坐标为 ,则 的长度为( ) A、 B、 C、 D、3. 一个矩形按如图1的方式分割成三个直角三角形,最小三角形的面积为S1 , 把较大两个三角形纸片按图2方式放置,图2中的阴影部分面积为S2 , 若S2=2S1 , 则矩形的长宽之比( )
A、 B、 C、 D、3. 一个矩形按如图1的方式分割成三个直角三角形,最小三角形的面积为S1 , 把较大两个三角形纸片按图2方式放置,图2中的阴影部分面积为S2 , 若S2=2S1 , 则矩形的长宽之比( ) A、2 B、 C、 D、4. 如图,四边形ABCD内接于.若 , 则的度数与BC的长分别为( )
A、2 B、 C、 D、4. 如图,四边形ABCD内接于.若 , 则的度数与BC的长分别为( ) A、 B、 C、 D、5. 如图,在正六边形ABCDEF中, , 点O在对角线AD上, , 以O为圆心,OB为半径画弧,分别交AB,AF于点M,N.则的长为( )
A、 B、 C、 D、5. 如图,在正六边形ABCDEF中, , 点O在对角线AD上, , 以O为圆心,OB为半径画弧,分别交AB,AF于点M,N.则的长为( ) A、 B、 C、 D、6. 如图,在中, , 以其三边为边向外作正方形,连接 , 交于点P,过点P作于点R.若 , , 则的值为( )
A、 B、 C、 D、6. 如图,在中, , 以其三边为边向外作正方形,连接 , 交于点P,过点P作于点R.若 , , 则的值为( ) A、10 B、11 C、 D、7. 如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )
A、10 B、11 C、 D、7. 如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )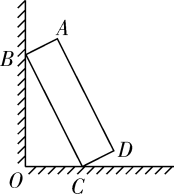 A、asinx+bsinx B、acosx+bcosx C、asinx+bcosx. D、acosx+bsinx8. 如图,为了测量某建筑物 的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡行走100米至坡顶D处,再从D处沿水平方向继续前行若干米到点E处,在E点测得该建筑物顶端C的仰角为59°,建筑物底端B的俯角为 , 点A、B、C、D、E在同一平面内,斜坡的坡度 .根据以上数据,计算出建筑物BC的高度约为(结果精确到1.参考数据: , , )( )
A、asinx+bsinx B、acosx+bcosx C、asinx+bcosx. D、acosx+bsinx8. 如图,为了测量某建筑物 的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡行走100米至坡顶D处,再从D处沿水平方向继续前行若干米到点E处,在E点测得该建筑物顶端C的仰角为59°,建筑物底端B的俯角为 , 点A、B、C、D、E在同一平面内,斜坡的坡度 .根据以上数据,计算出建筑物BC的高度约为(结果精确到1.参考数据: , , )( ) A、158米 B、161米 C、159米 D、160米9. 小明使用测角仪在甲楼底端A处测得熊猫C处的仰角为53°,在甲楼B处测得熊猫C处的仰角 已知AB=4.5米,则熊猫C处距离地面AD的高度为( )(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
A、158米 B、161米 C、159米 D、160米9. 小明使用测角仪在甲楼底端A处测得熊猫C处的仰角为53°,在甲楼B处测得熊猫C处的仰角 已知AB=4.5米,则熊猫C处距离地面AD的高度为( )(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33) A、13.6 B、18.1 C、17.3 D、16.810. 如图,建筑工地划出了三角形安全区 , 一人从点出发,沿北偏东53°方向走50m到达C点,另一人从B点出发沿北偏西53°方向走100m到达C点,则点A与点B相距( )
A、13.6 B、18.1 C、17.3 D、16.810. 如图,建筑工地划出了三角形安全区 , 一人从点出发,沿北偏东53°方向走50m到达C点,另一人从B点出发沿北偏西53°方向走100m到达C点,则点A与点B相距( ) A、 B、 C、 D、130m
A、 B、 C、 D、130m二、填空题(每空3分,共33分)
-
11. 如图,在正方形中,点E在上, , 连接 , 取中点F,过F作且使得 , 连接并延长,将绕点C旋转到 , 当 , , 三点共线且时,.
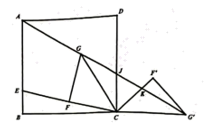 12. 如图1,是一幅椅子和花架相互转化的实物图.放置在水平地面上的椅子示意图如图2所示,在矩形ABCD中,点E在BC上,点F,G在CD上,G是CF的中点,隔板FH∥GI∥BC,分别交DE于点H,I,现将该椅子的左边部分JCDE绕着点E顺时针旋转180°得到一个花架,如图3所示,此时点J落在地面上的点J'处,点C,H的对应点分别为点C',H',已知AB=46cm,BC=37cm,BE=14cm,则点J离地面的距离是 cm;若点J',C',H'在同一直线上,tan∠AJ'C'=6,则隔板GI的长是 cm.
12. 如图1,是一幅椅子和花架相互转化的实物图.放置在水平地面上的椅子示意图如图2所示,在矩形ABCD中,点E在BC上,点F,G在CD上,G是CF的中点,隔板FH∥GI∥BC,分别交DE于点H,I,现将该椅子的左边部分JCDE绕着点E顺时针旋转180°得到一个花架,如图3所示,此时点J落在地面上的点J'处,点C,H的对应点分别为点C',H',已知AB=46cm,BC=37cm,BE=14cm,则点J离地面的距离是 cm;若点J',C',H'在同一直线上,tan∠AJ'C'=6,则隔板GI的长是 cm. 13. 飞机导航系统的正常工作离不开人造卫星的信号传输(如图1).五颗同轨道同步卫星,其位置 , , , , , 如图2所示.是它们的运行轨道,弧度数为 , 点到点和点的距离相等,于 , 交于 , 交于 , 连结 , , 已知一架飞机从飞到的直线距离为4千公里,则轨道的半径为千公里,当时,则线段 , 的长度之和为 千公里.
13. 飞机导航系统的正常工作离不开人造卫星的信号传输(如图1).五颗同轨道同步卫星,其位置 , , , , , 如图2所示.是它们的运行轨道,弧度数为 , 点到点和点的距离相等,于 , 交于 , 交于 , 连结 , , 已知一架飞机从飞到的直线距离为4千公里,则轨道的半径为千公里,当时,则线段 , 的长度之和为 千公里.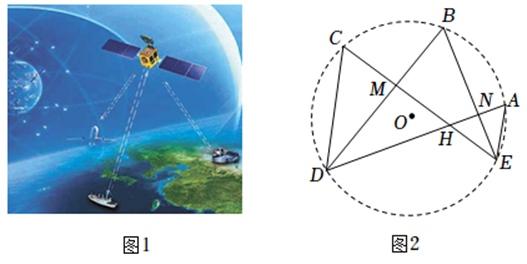 14. 衢州儿童公园有摩天轮,水上乐园等娱乐设施,其中的摩天轮半径为20米,水上乐园的最高处到地面的距离为32米;如图,当摩天轮的座舱A旋转至与水上乐园最高处高度相同时,地面某观测点P与座舱A,摩天轮圆心O恰好在同一条直线上,此时测得 , 则的距离为米;此时另一座舱B位于摩天轮最低点,摩天轮旋转一周要12分钟,若摩天轮继续逆时针旋转一周,当从座舱A观测座舱B的俯角为45°时,经过了分钟.
14. 衢州儿童公园有摩天轮,水上乐园等娱乐设施,其中的摩天轮半径为20米,水上乐园的最高处到地面的距离为32米;如图,当摩天轮的座舱A旋转至与水上乐园最高处高度相同时,地面某观测点P与座舱A,摩天轮圆心O恰好在同一条直线上,此时测得 , 则的距离为米;此时另一座舱B位于摩天轮最低点,摩天轮旋转一周要12分钟,若摩天轮继续逆时针旋转一周,当从座舱A观测座舱B的俯角为45°时,经过了分钟.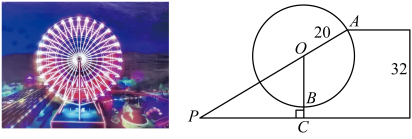 15. 如图,岸边堤坝和湖中分别伫立着甲、乙两座电线塔,甲塔底 和堤坝 段均与水平面 平行, 为 中点, 米, 米.某时刻甲塔顶
15. 如图,岸边堤坝和湖中分别伫立着甲、乙两座电线塔,甲塔底 和堤坝 段均与水平面 平行, 为 中点, 米, 米.某时刻甲塔顶 影子恰好落在斜坡底端 处,此时小章测得2米直立杆子的影长为1米.随后小章乘船行驶至湖面点 处,发现点 , , 三点共线,并在 处测得甲塔底 和乙塔顶 的仰角均为 ,则塔高 的长为米;若小章继续向右行驶10米至点 ,且在 处测得甲、乙两塔顶 , 的仰角均为 .若点 , , , 在同一水平线上, ,则甲、乙两塔顶 , 的距离为米.(参考数据: , , , )
影子恰好落在斜坡底端 处,此时小章测得2米直立杆子的影长为1米.随后小章乘船行驶至湖面点 处,发现点 , , 三点共线,并在 处测得甲塔底 和乙塔顶 的仰角均为 ,则塔高 的长为米;若小章继续向右行驶10米至点 ,且在 处测得甲、乙两塔顶 , 的仰角均为 .若点 , , , 在同一水平线上, ,则甲、乙两塔顶 , 的距离为米.(参考数据: , , , )
 16. 一款闭门器按如图1所示安装,支点A,C分别固定在门框和门板上,门宽 , 摇臂 , 连杆 , 闭门器工作时,摇臂、连杆和长度均固定不变.如图2,当门闭合时, , 则的长为cm.如图3,门板绕点O旋转,当时,点D到门框的距离 , 则的长为cm.
16. 一款闭门器按如图1所示安装,支点A,C分别固定在门框和门板上,门宽 , 摇臂 , 连杆 , 闭门器工作时,摇臂、连杆和长度均固定不变.如图2,当门闭合时, , 则的长为cm.如图3,门板绕点O旋转,当时,点D到门框的距离 , 则的长为cm.
三、解答题(共8题,共67分)
-
17. 为测量学校后山高度,数学兴趣小组活动过程如下:
 (1)、测量坡角
(1)、测量坡角如图1,后山一侧有三段相对平直的山坡 , 山的高度即为三段坡面的铅直高度之和,坡面的长度可以直接测量得到,要求山坡高度还需要知道坡角大小.
如图2,同学们将两根直杆的一端放在坡面起始端A处,直杆沿坡面方向放置,在直杆另一端N用细线系小重物G,当直杆与铅垂线重合时,测得两杆夹角的度数,由此可得山坡AB坡角的度数.请直接写出之间的数量关系.
(2)、测量山高同学们测得山坡的坡长依次为40米,50米,40米,坡角依次为;为求 , 小熠同学在作业本上画了一个含角的(如图3),量得 . 求山高 . ( , 结果精确到1米)
(3)、测量改进由于测量工作量较大,同学们围绕如何优化测量进行了深入探究,有了以下新的测量方法.

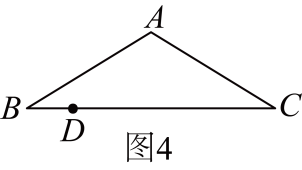
如图4,5,在学校操场上,将直杆NP置于的顶端,当与铅垂线重合时,转动直杆 , 使点N,P,D共线,测得的度数,从而得到山顶仰角 , 向后山方向前进40米,采用相同方式,测得山顶仰角;画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米,再画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米.已知杆高MN为米,求山高 . (结果用不含的字母表示)
18. 如图,在中, , .点D是直线上一动点.过点D作 , 满足点E在上方, , 以、为邻边作.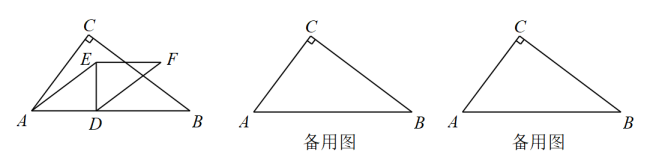 (1)、求的长以及点C到的距离;(2)、设线段与边交于点M,线段与边交于点N.当时,求的长;(3)、连接 , 沿直线分割 , 当分割的两部分可以拼成一个不重叠无缝隙的三角形时,求的长.19. 如图,光从空气斜射入水中,入射光线射到水池的水面点后折射光线射到池底点处,入射角 , 折射角;入射光线射到水池的水面点后折射光线射到池底点处,入射角 , 折射角 , 、为法线入射光线、和折射光线、及法线、都在同一平面内,点到直线的距离为米.
(1)、求的长以及点C到的距离;(2)、设线段与边交于点M,线段与边交于点N.当时,求的长;(3)、连接 , 沿直线分割 , 当分割的两部分可以拼成一个不重叠无缝隙的三角形时,求的长.19. 如图,光从空气斜射入水中,入射光线射到水池的水面点后折射光线射到池底点处,入射角 , 折射角;入射光线射到水池的水面点后折射光线射到池底点处,入射角 , 折射角 , 、为法线入射光线、和折射光线、及法线、都在同一平面内,点到直线的距离为米. (1)、求的长;结果保留根号(2)、如果米,求水池的深参考数据:取 , 取 , 取 , 取 , 取 , 取 , 取 , 取20. 为了监控危险路段的车辆行驶情况,通常会设置电子眼进行区间测速.如图电子眼位于点P处,离地面的铅垂高度PQ为11米;离坡AB的最短距离是11.2米,坡AB的坡比为3:4;电子眼照射在A 处时,电子眼的俯角为30°,电子眼照射在坡角点B处时,电子眼的俯角为70°.(A、B、P、Q在同一平面内)
(1)、求的长;结果保留根号(2)、如果米,求水池的深参考数据:取 , 取 , 取 , 取 , 取 , 取 , 取 , 取20. 为了监控危险路段的车辆行驶情况,通常会设置电子眼进行区间测速.如图电子眼位于点P处,离地面的铅垂高度PQ为11米;离坡AB的最短距离是11.2米,坡AB的坡比为3:4;电子眼照射在A 处时,电子眼的俯角为30°,电子眼照射在坡角点B处时,电子眼的俯角为70°.(A、B、P、Q在同一平面内) (1)、求路段BQ的长;(sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)(2)、求路段AB的长;(≈1.7,结果保留整数)(3)、如图的这辆车看成矩形KLNM,车高2米,当PA过M点时开始测速,PB过M点时结束测速,若在这个测速路段车辆所用的时间是1.5秒.该路段限速5米/秒,计算说明该车是否超速?21. 如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度D点处时,无人机测得操控者A的俯角为 , 测得小区楼房顶端点C处的俯角为 . 已知操控者A和小区楼房之间的距离为45米,小区楼房的高度为米.
(1)、求路段BQ的长;(sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)(2)、求路段AB的长;(≈1.7,结果保留整数)(3)、如图的这辆车看成矩形KLNM,车高2米,当PA过M点时开始测速,PB过M点时结束测速,若在这个测速路段车辆所用的时间是1.5秒.该路段限速5米/秒,计算说明该车是否超速?21. 如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度D点处时,无人机测得操控者A的俯角为 , 测得小区楼房顶端点C处的俯角为 . 已知操控者A和小区楼房之间的距离为45米,小区楼房的高度为米. (1)、求此时无人机的高度;(2)、在(1)条件下,若无人机保持现有高度沿平行于的方向,并以5米/秒的速度继续向前匀速飞行.问:经过多少秒时,无人机刚好离开了操控者的视线?(假定点A,B,C,D都在同一平面内.参考数据: , . 计算结果保留根号)22. 小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.
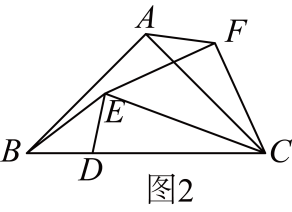
(1)、求此时无人机的高度;(2)、在(1)条件下,若无人机保持现有高度沿平行于的方向,并以5米/秒的速度继续向前匀速飞行.问:经过多少秒时,无人机刚好离开了操控者的视线?(假定点A,B,C,D都在同一平面内.参考数据: , . 计算结果保留根号)22. 小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm. (1)、求∠CAO'的度数.(2)、显示屏的顶部B'比原来升高了多少?(3)、如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?23. 爱好思考的小实在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”,如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC=b,AB=c.
(1)、求∠CAO'的度数.(2)、显示屏的顶部B'比原来升高了多少?(3)、如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?23. 爱好思考的小实在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”,如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC=b,AB=c.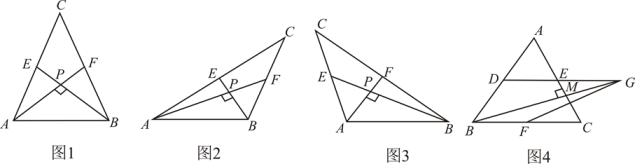 (1)、【特例探究】
(1)、【特例探究】①如图1,当tan∠PAB=1, 时,a= , b=.
②如图2,当∠PAB=30°,c=4时,a= , b=.
(2)、【归纳证明】请你观察(1)中的计算结果,猜想 、 、 三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)、【拓展证明】如图4,在△ABC中, , ,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至点G,使得GE=DE,连结BG.若BG⊥AC于点M时,求GF的长.
24. 【问题情境】如图,在中, , . 点D在边上将线段绕点D顺时针旋转得到线段(旋转角小于),连接 , , 以为底边在其上方作等腰三角形 , 使 , 连接 .(1)、【尝试探究】如图1,当时,易知;
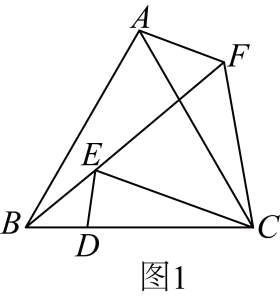
如图2,当时,则与的数量关系为;
 (2)、如图3,写出与的数量关系(用含α的三角函数表示).并说明理由;
(2)、如图3,写出与的数量关系(用含α的三角函数表示).并说明理由; (3)、【拓展应用】
(3)、【拓展应用】如图4,当 , 且点B , E , F三点共线时.若 , , 请直接写出的长.