（提升卷）1.1 锐角三角函数-2023-2024年浙教版数学九年级下册同步测试

试卷更新日期：2023-09-10 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 在Rt△ABC中，∠C＝90°，∠B＝35°，AB＝7，则BC的长为（）

A、7sin 35° B、7cos 35° C、7tan 35° D、 $\frac{7}{\cos 35 °}$

查看试题解析
2. 在直角ΔABC中，已知∠C＝90°， $sinA = \frac{1}{3}$ ，求cosA=（）

A、 $\frac{\sqrt{10}}{10}$ B、 $\frac{\sqrt{2}}{4}$ C、 $\frac{2 \sqrt{2}}{3}$ D、 $2 \sqrt{2}$

查看试题解析
3. 一配电房示意图如图所示，它是一个轴对称图形，已知 $B C = 6 m$ ，房顶A离地面 $E F$ 的高度为 $6 m$ ，则 $t a n ∠ A B C$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $\frac{1}{3}$ D、3

查看试题解析
4. 如图， $△ A B C$ 的顶点都是正方形网格中的格点，则 $cos ∠ A C B$ 等（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{3}{4}$ D、 $\frac{\sqrt{10}}{10}$

查看试题解析
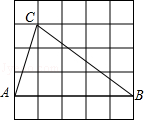5. 如图，在△ABC中，AB＝AC，BC＝8，E为AC边的中点，线段BE的垂直平分线交边BC于点D.设BD＝x，tan∠ACB＝y，则x与y满足关系式（　　）

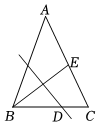A、x﹣y²＝3 B、2x﹣y²＝6 C、3x﹣y²＝9 D、4x﹣y²＝12

查看试题解析
6. 如图， $A B$ 是半圆的直径， $∠ A B C$ 的平分线分别交弦 $A C$ 和半圆于E和D，若 $B E = 2 D E$ ， $A B = 4$ ，则 $A E$ 长为（　　）

A、2 B、 $\sqrt{2} + 1$ C、 $\sqrt{6}$ D、 $\frac{4 \sqrt{3}}{3}$

查看试题解析
7. 如图，在圆O内有折线OABC，其中OA＝8，AB＝12，∠A＝∠B＝60°，则BC的长为（）

A、16 B、20 C、18 D、22

查看试题解析
8. 如图，已知点A（ $\sqrt{3}$ ，2）， B(0，1)，射线AB绕点A逆时针旋转30°，与x轴交于点C，则过A，B，C三点的二次函数y=ax²+bx+1中a，b的值分别为（）

A、 $a = 2 ， b = - \frac{5}{3} \sqrt{3}$ B、 $a = \frac{1}{2} ， b = - \frac{\sqrt{3}}{6}$ C、 $a = 3 ， b = - \frac{8}{3} \sqrt{3}$ D、 $a = - \frac{1}{3} ， b = \frac{2}{3} \sqrt{3}$

查看试题解析
9. 如图，在⊙O中，弦AB的长是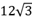 cm，弦AB的弦心距为6cm，E是⊙O优弧AEB上一点.则∠AEB的度数为（）

A、60° B、45° C、30° D、80°

查看试题解析
10. 在Rt△ABC中，∠C=90°，若sinA= $\frac{2}{3}$ ，则tanB=（）

A、 $\frac{3 \sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{3}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{\sqrt{5}}{2}$

查看试题解析

二、填空题（每空4分，共24分）

11. 已知 $α$ 为锐角，且 $t a n (α - 10 °) = \frac{\sqrt{3}}{3}$ ，则锐角 $α$ 的度数是.

查看试题解析
12. 已知∠A、∠B、∠C是△ABC的三个内角，若|sinA﹣ $\frac{\sqrt{3}}{2}$ |+（cosB﹣ $\frac{\sqrt{3}}{2}$ ）²=0，则∠C的度数是

查看试题解析
13. 已知α是锐角且tanα= $\frac{3}{4}$ ，则sinα+cosα=

查看试题解析
14. 在△ABC中，AB=AC=5，BC=8，若∠BPC= $\frac{1}{2}$ ∠BAC，tan∠BPC= ．

查看试题解析
15. 如图，已知在平面直角坐标系xOy中，点A在x轴的负半轴上，点B在y轴的负半轴上， $t a n ∠ A B O = 3$ ，以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是 $y = \frac{1}{x}$ ，则图象经过点D的反比例函数的解析式是.

查看试题解析
16. 在半径为1的圆中，长度等于 $\sqrt{2}$ 的弦所对的圆周角是度

查看试题解析

三、解答题（共8题，共66分）

17.

(1)、计算： $2 \tan 60 ° \times \cos 30 ° - 4 \sin^{2} 60 °$ ；

(2)、已知二次函数顶点为 $(1 ， 2)$ ，经过点 $(0 ， 1)$ ，求该二次函数的一般式.

查看试题解析
18. 先化简 $(1 - \frac{1}{a + 1}) \div \frac{a}{a^{2} - 1}$ ，然后再从sin30°，1， ${(- \frac{1}{2})}^{- 1}$ 这三个数中选取一个你认为合适的数作为a的值代入求值.

查看试题解析

19. 为了充分利用四边形余料，小明设计了不同的方案裁剪正方形，裁剪方案与数据如下表：

方案设计	方案1	方案2
裁剪方案示意图
说明	图中的正方形 $A E F G$ 和正方形 $M N P Q$ 四个顶点都在原四边形的边上
测量数据	$A D = 9 d m$ ， $C D = 2 d m$ ， $A B = 14 d m$ ， $∠ A = ∠ D = 90 °$ ；
任务1：探寻边角	填空： $B C =$ ▲ $d m$ ， $s i n B =$ ▲ ；
任务2：比较面积	计算或推理：正方形 $A E F G$ 和正方形 $M N P Q$ 边长之比；
任务3：应用实践	若在 $△ B E F$ 余料上再截取一个最大正方形，正方形的边长为 ▲ $d m$ .

查看试题解析

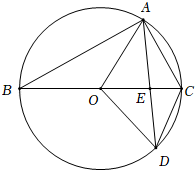
20. 芳芳家有一种伸缩挂衣架（如图1），伸缩挂衣架中有3个菱形组成，每个菱形边长为10cm.伸缩挂衣架打开时，每个菱形的锐角度数为60°（如图2）；伸缩挂衣架收拢时，每个菱形的锐角度数从60°缩小为10°（如图3）.问：伸缩挂衣架从打开到收拢共缩短了多少cm?（结果精确到1cm，参考数据： $s i n 5 ° \approx 0.0872$ ， $c o s 5 ° \approx 0.9962$ ， $s i n 10 ° \approx 0.1736$ ， $c o s 10 ° \approx 0.9848$ ）.

查看试题解析
21. 如图，在Rt $△ A B C$ 中， $∠ A B C = 90 °$ ， $A B < B C$ .点D是 $A C$ 的中点，过点D作 $D E ⊥ A C$ 交 $B C$ 于点E.延长 $E D$ 至点F，使得 $D F = D E$ ，连接 $A E$ 、 $A F$ 、 $C F$ .

(1)、求证：四边形 $A E C F$ 是菱形；

(2)、若 $\frac{B E}{E C} = \frac{1}{4}$ ，则 $t a n ∠ B C F$ 的值为.

查看试题解析
22. 如图，AB是⊙O的直径，弦CD⊥AB于点E，连结AC，BC.

(1)、求证：∠ACO＝∠BCD；

(2)、若CD＝6，∠A＝30°，求阴影部分的面积.

查看试题解析
23. 在 $△ A B C$ 和 $△ B D E$ 中，点 $A ， B ， D$ 在同一直线上， $A C ⊥ A D ， B C ⊥ B E$ .

(1)、如图1，如果 $D E ⊥ A D$ ，求证： $△ A B C ∽ △ D E B$ ；

(2)、如果 $A D = 20$ ， $A C = 4$ ， $B E = \frac{1}{2} B C$ .
$①$ 如图2，当 $B E = D E$ 时，求 $A B$ 的长；
$②$ 如图3， $G$ 点是 $C A$ 延长线上一点，且 $A G = 8$ ，连结 $B G$ ，如果 $∠ G = ∠ D$ ，求 $t a n D$ 的值.

查看试题解析
24. 如图所示，已知 $B C$ 是⊙O的直径，A、D是⊙O上的两点，连接 $A D$ 、 $A C$ 、 $C D$ ，线段 $A D$ 与直径 $B C$ 相交于点E.

(1)、若 $∠ A C B ＝ 60 °$ ，求 $s i n ∠ A D C$ 的值.

(2)、当 $\overset{⌢}{C D} = \frac{1}{2} \overset{⌢}{A C}$ 时，
①若 $C E = \sqrt{2}$ ， $\frac{B C \cdot C E}{A B} = 2$ ，求 $∠ C O D$ 的度数.
②若 $C D ＝ 1$ ， $C B ＝ 4$ ，求线段 $C E$ 的长.

查看试题解析