(培优卷)1.1 锐角三角函数-2023-2024年浙教版数学九年级下册
试卷更新日期:2023-09-10 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,在边长相同的小正方形组成的网格中,点、、、都在这这些小正方形的顶点上,、相交于点 . 则的值是( )
 A、 B、 C、 D、2. 如图,一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28km/时的速度向正东航行,半小时到B处,在B处看见灯塔M在北偏东15°方向,此时,灯塔M与渔船的距离是( )
A、 B、 C、 D、2. 如图,一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28km/时的速度向正东航行,半小时到B处,在B处看见灯塔M在北偏东15°方向,此时,灯塔M与渔船的距离是( )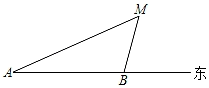 A、7km B、14km C、7km D、14km3. 下列计算错误的有( )
A、7km B、14km C、7km D、14km3. 下列计算错误的有( )① ;② ;③ ;④ .
A、1个 B、2个 C、3个 D、4个4. 下列式子正确的是( )A、 B、 C、 D、5. 如图,在平面直角坐标系xOy中,AB , CD , EF , GH是正方形OPQR边上的线段,点M在其中某条线段上,若射线OM与x轴正半轴的夹角为α,且sinα>cosα,则点M所在的线段可以是( ) A、AB和CD B、AB和EF C、CD和GH D、EF和GH6. 已知:a为锐角,且 =1则tana的值等于( )A、-1 B、2 C、3 D、2.57. 以下说法正确的是( )A、存在锐角 ,使得sin²+cos² >1 B、已知∠A为Rt△ABC的一个内角,且∠A<45°,则sinA<cosA C、在Rt△ABC中,∠C=90°,∠A,∠B为Rt△ABC的两个内角,则sinA不一定等于cosB D、存在锐角 ,使得sin ≥tan8. 在△ABC中,AB=12 ,AC=13,cosB= ,则BC的边长为( )A、7 B、8 C、8或17 D、7或179. 如图,在边长为的小正方形网格中,点都在这些小正方形的顶点上,相交于点 , 则( )
A、AB和CD B、AB和EF C、CD和GH D、EF和GH6. 已知:a为锐角,且 =1则tana的值等于( )A、-1 B、2 C、3 D、2.57. 以下说法正确的是( )A、存在锐角 ,使得sin²+cos² >1 B、已知∠A为Rt△ABC的一个内角,且∠A<45°,则sinA<cosA C、在Rt△ABC中,∠C=90°,∠A,∠B为Rt△ABC的两个内角,则sinA不一定等于cosB D、存在锐角 ,使得sin ≥tan8. 在△ABC中,AB=12 ,AC=13,cosB= ,则BC的边长为( )A、7 B、8 C、8或17 D、7或179. 如图,在边长为的小正方形网格中,点都在这些小正方形的顶点上,相交于点 , 则( ) A、 B、 C、 D、210. 如图是一张高脚木凳,AC∥EF∥GH,AB=CD,点E,G是AB的三等分点,已知EF与GH之间的距离为25cm,∠EGH=80°,则椅脚AB的长度为 cm( )
A、 B、 C、 D、210. 如图是一张高脚木凳,AC∥EF∥GH,AB=CD,点E,G是AB的三等分点,已知EF与GH之间的距离为25cm,∠EGH=80°,则椅脚AB的长度为 cm( ) A、 B、75sin80° C、 D、
A、 B、75sin80° C、 D、二、填空题(每题3分,共18分)
-
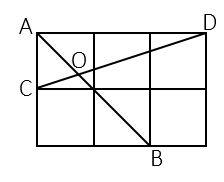
11. △ABC中,AD是BC边上的高,AD=4, , AB=8,则 .12. 已知:0°<α<90°,0°<β<90°且sinα= , tanβ= , 则cos(β﹣α)= .13. 在Rt△ABC中,∠C=90°,若cosB= ,则tanA= , 若此时△ABC的周长为48,那么△ABC的面积 .14. 如图,在边长为1的小正方形网格中,点A , B , C , D都在这些小正方形的顶点上,AB , CD相交于点O , 则cos∠BOD= .
 15. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是边AC的中点,点E,F在边AB上,当△DEF是等腰三角形,且底角的正切值是 时,△DEF腰长的值是 .
15. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是边AC的中点,点E,F在边AB上,当△DEF是等腰三角形,且底角的正切值是 时,△DEF腰长的值是 . 16. 如图为我国汉代数学家赵爽在注解《周髀算经》时给出的图形,人们称它为“赵爽弦图”.图形是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是120,小正方形面积是20,则 = .
16. 如图为我国汉代数学家赵爽在注解《周髀算经》时给出的图形,人们称它为“赵爽弦图”.图形是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是120,小正方形面积是20,则 = .
三、综合题(共8题,共72分)
-
17. 如图,半圆中,直径 , 点为弧的中点,点在弧上,连结并延长交的延长线于点 , 连结交于点 , 连结.
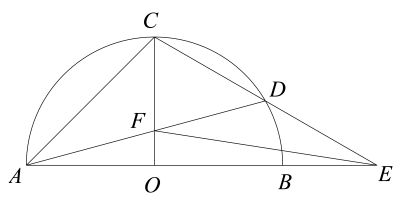 (1)、求证:.(2)、若点为中点,求的长.(3)、①面积与面积的差是定值吗?如果是,请求出该定值;若不是,请说明理由;
(1)、求证:.(2)、若点为中点,求的长.(3)、①面积与面积的差是定值吗?如果是,请求出该定值;若不是,请说明理由;②若 , 求的长.
18. 如图:

图1 图2
(1)、如图1,在△ABC中,∠ACB=2∠B,CD平分∠ACB,交AB于点D,DE∥AC,交BC于点E.①若DE=1,BD= , 求BC的长;
②试探究是否为定值.如果是,求出这个定值;如果不是,请说明理由.
(2)、如图2,∠CBG和∠BCF是△ABC的2个外角,∠BCF=2∠CBG,CD平分∠BCF,交AB的延长线于点D,DE∥AC,交CB的延长线于点E.记△ACD的面积为S1 , △CDE的面积为S2 , △BDE的面积为S3 . 若S1•S3=S22 , 求cos∠CBD的值.19. 如图,周长为22的矩形ABCD内接于⊙O,点E,F分别在边CD,BC上,AE平分∠FAD,EG∥AD,交AF于点G,延长AF交⊙O于点M,连结BM,tanM=. (1)、求AB,AD的长.(2)、记DE=x,GE=y,求y关于x的函数表达式.(3)、①连结EF,当∠GEF=∠GFE时,求OG+OE长.
(1)、求AB,AD的长.(2)、记DE=x,GE=y,求y关于x的函数表达式.(3)、①连结EF,当∠GEF=∠GFE时,求OG+OE长.②当点D关于直线AE的对称点D′恰好落在⊙O上时,求的值.
20. 如图,抛物线与x轴交于点 , 与y轴交于点B,在x轴上有一动点 , 过点E作x轴的垂线交直线AB于点N,交拋物线于点P,过点P作于点M.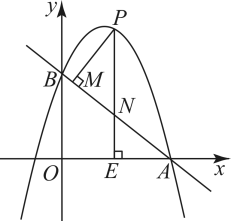 (1)、求a的值及.(2)、求的最大值.(3)、设的面积为 , 的面积为 , 若 , 求此时m的值.21. 如图,在锐角三角形中, , 以为直径的分别交于点 , 连接.
(1)、求a的值及.(2)、求的最大值.(3)、设的面积为 , 的面积为 , 若 , 求此时m的值.21. 如图,在锐角三角形中, , 以为直径的分别交于点 , 连接. (1)、若 , 求的度数;(2)、求证:;(3)、若半径为 , , 求四边形的面积(用含的代数式表示).22. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G.
(1)、若 , 求的度数;(2)、求证:;(3)、若半径为 , , 求四边形的面积(用含的代数式表示).22. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G. (1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .
(1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .①若 ,求 的周长.
②求 的最小值.
23. 定义:有两边之比为 的三角形叫做智慧三角形.(1)、如图1,在智慧三角形 中, 为 边上的中线,求 的值; (2)、如图2, 是⊙O的内接三角形, 为直径,过 的中点 作 交线段 于点 ,交⊙O于点 ,连结 交 于点 .
(2)、如图2, 是⊙O的内接三角形, 为直径,过 的中点 作 交线段 于点 ,交⊙O于点 ,连结 交 于点 .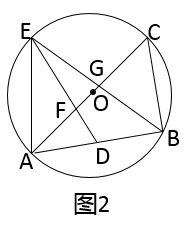
①求证: 是智慧三角形;
②设 ,若⊙O的半径为 ,求 关于 的函数表达式;
(3)、如图3,在(2)的条件下,当 时,求 的余弦值. 24. 在△ABC中,∠ABC=90°,N是AB延长线上一点,点M在BC上.
24. 在△ABC中,∠ABC=90°,N是AB延长线上一点,点M在BC上. (1)、【基础巩固】
(1)、【基础巩固】
如图1,若AB=BC,CN⊥AM,求证:BM=BN;(2)、【变式探究】
如图2,若AB=BC,过点B作BP⊥AM于点P,连接CP并延长交AB于点Q.求证:;
(3)、【拓展提高】
如图3,设=k(k≠1),M是BC的中点,过点B作BP⊥AM于点P,连接CP并延长交AB于点Q.求tan∠BPQ的值(用含k的式子表示).