2023-2024学年初中数学七年级上册 4.3.2 角的度量与计算 同步分层训练培优卷(湘教版)
试卷更新日期:2023-09-10 类型:同步测试
一、选择题
-
1. 已知一个角是40°,则这个角的余角的度数是( )A、30° B、40° C、50° D、60°2. 甲、乙、丙、丁四位同学解决以下问题,其中作图正确的是( )

问题:某旅游景区内有一块三角形绿地ABC,如图所示,先要在道路AB边上建一个休息点M,使它到AC和BC两边的距离相等,在图中确定休息点M的位置.
 A、甲 B、乙 C、丙 D、丁3. 如图,点在直线上,、分别平分、 , 则图中互为余角的有( )对
A、甲 B、乙 C、丙 D、丁3. 如图,点在直线上,、分别平分、 , 则图中互为余角的有( )对 A、1 B、2 C、3 D、44. 观察图中尺规作图痕迹,下列结论不正确的是( )
A、1 B、2 C、3 D、44. 观察图中尺规作图痕迹,下列结论不正确的是( )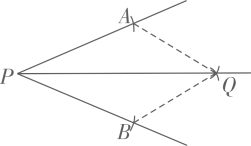 A、为的平分线 B、 C、点A、B到的距离不相等 D、5. 下列说法正确的是( )
A、为的平分线 B、 C、点A、B到的距离不相等 D、5. 下列说法正确的是( )①等角的余角相等;②若∠AOC=∠AOB,则射线OC为∠AOB平分线;③若∠α与∠β互余,则∠α的补角比∠β大90°.
A、①②③ B、①② C、①③ D、②③6. 如图,码头A在码头B的正西方向,甲、乙两船分别从A、B 同时出发,并以等速驶向某海域,甲的航向是北偏东 , 为避免行进中甲、乙相撞,则乙的航向不能是( )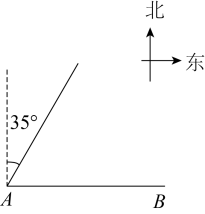 A、北偏东 B、北偏西 C、北偏东 D、北偏西7. 如图,用尺规作出了 , 关于作图痕迹,下列说法错误的是( )
A、北偏东 B、北偏西 C、北偏东 D、北偏西7. 如图,用尺规作出了 , 关于作图痕迹,下列说法错误的是( )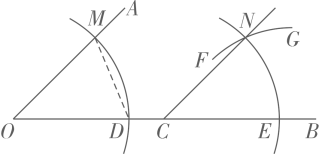 A、弧是以点O为圆心,任意长为半径的弧 B、弧是以点C为圆心,为半径的弧 C、弧是以点E为圆心,为半径的弧 D、弧是以点E为圆心,为半径的弧8. 如图,直线相交于点O,于点O,若 , 则等于( )
A、弧是以点O为圆心,任意长为半径的弧 B、弧是以点C为圆心,为半径的弧 C、弧是以点E为圆心,为半径的弧 D、弧是以点E为圆心,为半径的弧8. 如图,直线相交于点O,于点O,若 , 则等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分,∠COE若 , 则∠DOE=.
 10. 如图,直线相交于点 , 若 , 则的度数为 .
10. 如图,直线相交于点 , 若 , 则的度数为 .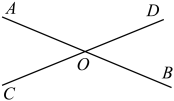 11. 把命题“等角的余角相等”改写成“如果……,那么……”的形式是 .12. 已知 , 如图1,过作射线、 , 如图2,过作射线、 , 使 , , , , 则 .
11. 把命题“等角的余角相等”改写成“如果……,那么……”的形式是 .12. 已知 , 如图1,过作射线、 , 如图2,过作射线、 , 使 , , , , 则 .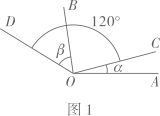
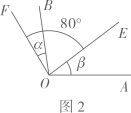 13. 如图1,射线在的内部,图中共有3个角: , 和 , 若其中有一个角的度数是另一个角度数的两倍,则称射线是的“巧分线”,如图2,若 , 且射线是的“巧分线”,则 .
13. 如图1,射线在的内部,图中共有3个角: , 和 , 若其中有一个角的度数是另一个角度数的两倍,则称射线是的“巧分线”,如图2,若 , 且射线是的“巧分线”,则 .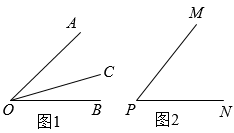
三、解答题
-
14. 如图,直线 , 相交于点O,平分 , . 若 , 求的度数.
 15. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数.
15. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数.
四、作图题
-
16. 图①、图②、图③均是由小正方形组成的的网格,的三个顶点A、B、C均在格点(网格线的交点)上,请按要求在给定的网格中,仅用无刻度的直尺,分别按下列要求作图,保留作图痕迹,不写画法.
 (1)、在图①中的上确定一点D , 连结 , 使 .(2)、在图②中的上确定一点E , 连结 , 使 .(3)、在图③中的上确定一点F , 连结 , 使 .
(1)、在图①中的上确定一点D , 连结 , 使 .(2)、在图②中的上确定一点E , 连结 , 使 .(3)、在图③中的上确定一点F , 连结 , 使 .五、综合题
-
17. 已知 , 在内部, .
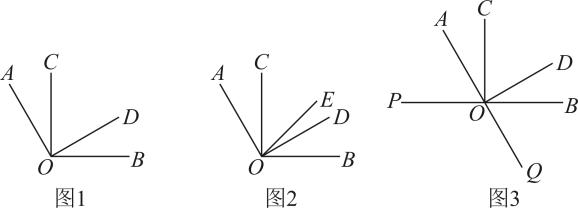 (1)、如图1,若 , 求的度数;(2)、如图2,若平分 , 请说明:;(3)、如图3,若在的外部分别作 , 的余角 , , 求的度数.18. 新定义:若α的度数是β的度数的n倍,则α叫做β的n倍角.
(1)、如图1,若 , 求的度数;(2)、如图2,若平分 , 请说明:;(3)、如图3,若在的外部分别作 , 的余角 , , 求的度数.18. 新定义:若α的度数是β的度数的n倍,则α叫做β的n倍角.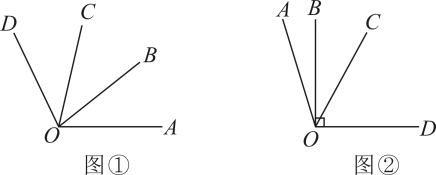 (1)、若 , 请直接写出的3倍角的度数;(2)、如图①,若 , 请直接写出图中的所有2倍角;(3)、如图②,若是的3倍角,是的4倍角,且 , 求的度数.19. 如图所示,以直线上的一点为端点,在直线的上方作射线 , 使 , 将一块直角三角尺的直角顶点放在点处,且直角三角尺在直线的上方.设 .
(1)、若 , 请直接写出的3倍角的度数;(2)、如图①,若 , 请直接写出图中的所有2倍角;(3)、如图②,若是的3倍角,是的4倍角,且 , 求的度数.19. 如图所示,以直线上的一点为端点,在直线的上方作射线 , 使 , 将一块直角三角尺的直角顶点放在点处,且直角三角尺在直线的上方.设 . (1)、当n=30时,求的大小;(2)、当恰好平分时,求n的值;(3)、当时,嘉嘉认为与的差为定值,淇淇认为与的和为定值,且二人求得的定值相同,均为 , 老师说,要使两人的说法都正确,需要对n分别附加条件.请你补充这个条件:
(1)、当n=30时,求的大小;(2)、当恰好平分时,求n的值;(3)、当时,嘉嘉认为与的差为定值,淇淇认为与的和为定值,且二人求得的定值相同,均为 , 老师说,要使两人的说法都正确,需要对n分别附加条件.请你补充这个条件:当满足时,;
当满足时, .
-