2023-2024学年初中数学七年级上册 4.2 线段/射线/直线同步分层训练培优卷(湘教版)

试卷更新日期：2023-09-10 类型：同步测试

进入出卷网下载

一、选择题

1. 要在墙上钉牢一根木条，至少要钉两颗钉子.能正确解释这一现象的数学知识是（）

A、两点之间，线段最短 B、垂线段最短 C、两点确定一条直线 D、经过一点有且只有一条直线与已知直线垂直

查看试题解析
2. 如图，已知点A，B在直线l两侧，在直线l上找一点，使得该点到点A与点B的距离之和最小，则这个点是（）

A、M B、N C、P D、Q

查看试题解析
3. 下列说法正确的个数是（）
①射线AB与射线BA是同一条射线；②两点确定一条直线；③两点之间直线最短；④若AB＝BC，则点B是AC的中点．

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 已知A，B，C三点在数轴上从左向右依次排列，且AC＝3AB＝6，若B为原点，则点A所表示的数是（）

A、-4 B、4 C、-2 D、2

查看试题解析
5. 如图，已知A，B（B在A的左侧）是数轴上的两点，点A对应的数为4，且 $A B = 6$ ，动点P从点A出发，以每秒2个单位长度的速度沿数轴向左运动，在点P的运动过程中，M，N始终为AP，BP的中点，设运动时间为 $t (t > 0)$ 秒，则下列结论中正确的有（）
①B对应的数是2；②点P到达点B时， $t = 3$ ；③ $B P = 2$ 时， $t = 2$ ；④在点P的运动过程中，线段MN的长度不变．

A、①③④ B、②③④ C、②③ D、②④

查看试题解析
6. 若线段 $A_{1} A_{2} = 2$ ，在线段 $A_{1} A_{2}$ 的延长线上取一点 $A_{3}$ ，使 $A_{2}$ 是 $A_{1} A_{3}$ 的中点；在线段 $A_{1} A_{3}$ 的延长线上取一点 $A_{4}$ ，使 $A_{3}$ 是 $A_{1} A_{4}$ 的中点；在线段 $A_{1} A_{4}$ 的延长线上取一点 $A_{5}$ ，使 $A_{4}$ 是 $A_{1} A_{5}$ 的中点……，按这样操作下去，线段 $A_{20} A_{21}$ 的长度为（）

A、 $2^{18}$ B、 $2^{19}$ C、 $2^{20}$ D、 $2^{21}$

查看试题解析
7. 如图，在平面直角坐标系上有一个质点 $A_{0} (- 1 ， 0)$ ，质点 $A_{0}$ 第一次跳动至点 $A_{1} (1 ， 1)$ ，第二次跳动至点 $A_{2} (- 2 ， 1)$ ，第三次跳动至点 $A_{3} (2 ， 2)$ ，第四次跳动至点 $A_{4} (- 3 ， 2)$ ， ……依此规律跳动下去，则点 $A_{2023}$ 与点 $A_{2024}$ 之间的距离是（）

A、2023 B、2025 C、2027 D、2029

查看试题解析

二、填空题

8. 已知点 $A (4 ， - 3)$ ， $B (4 ， 5)$ ，则A，B两点间的距离为．

查看试题解析
9. 已知数轴上有A、B两点，A点表示的数是-2，A、B两点的距离为3个单位长度，则满足条件的点B表示的数是 .

查看试题解析
10. 点 $A (3 ， 1)$ 关于点 $P (1 ， 0)$ 的对称点B的坐标是．

查看试题解析
11. 如图，已知点A、B、C是数轴上三点，O为原点.点C对应的数为6， $B C = 4$ ， $A B = 12$ .动点P、Q分别同时从A、C出发，分别以每秒6个单位和3个单位的速度沿数轴正方向运动.M为 $A P$ 的中点，N在线段 $C Q$ 上，且 $C N = \frac{1}{3} C Q$ ，设运动时间为 $t (t > 0)$ .

(1)、点M对应的数为（用含t的式子表示）；

(2)、当t为时，P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.

查看试题解析
12. 如图，数轴上O，A两点的距离为4，一动点P从点A出发，第1次跳动到 $A O$ 的中点 $A_{1}$ 处，第2次从点 $A_{1}$ 跳动到 $A_{1} O$ 的中点 $A_{2}$ 处，第3次从点 $A_{2}$ 跳动到 $A_{2} O$ 的中点 $A_{3}$ 处，按照这样的规律继续跳动到点 $A_{4}$ ， $A_{5}$ ， $A_{6}$ ， …， $A_{n}$ 处，那么线段 $A_{n} A$ 的长度为．

查看试题解析

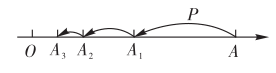
三、解答题

13. 数轴上，表示 $- 4$ 与2的点之间的距离是 $2 - (- 4) = 6$ ，表示 $- 4$ 与 $- 1$ 的点之间的距离是 $- 1 - (- 4) = 3$ ，即数轴上两点之间的距离等于较大数与较小数的差，若不知道数轴上两数的大小，则表示数 $m$ 与 $n$ 的点之间的距离可以表示为 $| m - n |$ ，利用上述结论解决如下问题．
若 $| x - 5 | = 3$ ，求 $x$ 的值．

查看试题解析
14. 如图1所示，两个村庄A，B在河流l的两侧，现要在河边修建一个水泵站，同时向A、B两村供水，要使所铺设的管道最短，水泵站Р应该建在什么位置?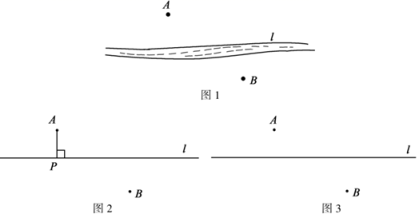

把河流 $l$ 近似看作直线 $l$ ，如图2所示．小明提出了这样的方案：过点A作直线 $l$ 的垂线段AP，则点P为水泵站的位置．你同意小明的方案吗?若同意，请说明理由．若不同意，那么你认为水泵站Р应该建在什么位置?请在图3中作出来，并说明依据．

查看试题解析

四、综合题

15. 如图，有两条线段， $A B = 2$ （单位长度）， $C D = 1$ （单位长度）在数轴上，点A在数轴上表示的数是 $- 12$ ，点D在数轴上表示的数是15．

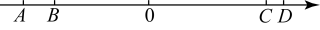(1)、点B在数轴上表示的数是，点C在数轴上表示的数是；

(2)、若线段 $A B$ 以1个单位长度/秒的速度向左匀速运动，同时线段 $C D$ 以2个单位长度秒的速度也向左匀速运动，设运动时间为t秒，当t为何值时，点B与点C之间的距离为1个单位长度？

(3)、若线段 $A B$ 、线段 $C D$ 分别以1个单位长度/秒、2个单位长度/秒的速度同时向左匀速运动，与此同时，动点P从 $- 15$ 出发，以4个单位长度/秒的速度向右匀速运动．设运动时间为t秒，当 $0 < t < 5$ 时， $2 A C - \frac{1}{3} P D$ 的值是否发生变化？若不变化，求出这个定值，若变化，请说明理由．

查看试题解析
16. 先阅读下面一段文字，再回答问题：已知在平面直角坐标系xOy中对于任意两点P₁（x₁ ， y₁）与R（x₂ ， y₂）的“识别距离”，给出如下定义：若|x₁-x₂|≥|y₁-y₂|，则点，P₁（x₁ ， y₁）与P₂（x₂ ， y₂）的“识别距离”为|x₁-x₂|；若|x₁-x₂||＜|y₁-y₂|，则点P₁（x₁ ， y1）与P₂（x₂ ， y₂）的“识别距离”为|y₁-y₂|；

(1)、已知点A（-1，0）；B为y轴上的动点．
①若点A与点B的“识别距离”为3，写出满足条件的点B的坐标．
②直接写出点A与点B的“识别距离”的最小值为．

(2)、已知点C（m， $\frac{3}{4}$ m+3）；D（1，1），求点C与点D的“识别距离”的最小值及相应的点C的坐标．

查看试题解析

2023-2024学年初中数学七年级上册 4.2 线段/射线/直线 同步分层训练培优卷(湘教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学七年级上册 4.2 线段/射线/直线同步分层训练培优卷(湘教版)