2023-2024学年初中数学七年级上册 4.2 线段/射线/直线 同步分层训练基础卷(湘教版)
试卷更新日期：2023-09-10 类型：同步测试
一、选择题
-
1. 把弯曲的道路改直就能缩短路程，下列数学语言解释正确的是（ ）A、垂线段最短 B、两点确定一条直线 C、两点之间线段最短 D、对顶角相等2. 如图，下列说法错误的是（ ）
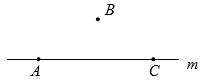A、点在直线上，点在直线外 B、射线与射线不是同一条射线 C、直线还可以表示为直线或直线 D、图中有直线3条，射线2条，线段1条3. 数轴上表示数12和表示数-4的两点之间的距离是（ ）A、8 B、-8 C、16 D、-164. 将一根木条固定在墙上至少需要两枚钉子，这一生活经验运用到的数学知识是（ ）
A、两点确定一条直线 B、两点之间线段最短 C、在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线 D、连结直线外一点与直线上各点的所有连线中，垂线段最短5. 如图，数轴上点M，P，N分别表示数m，m+n，n，那么原点的位置是（ ）
A、在线段MP上 B、在线段PN上 C、在点M的左侧 D、在点N的右侧6. 在下列生活、生产现象中，可以用基本事实“两点之间，线段最短”来解释的是（ ）①用两颗钉子就可以把木条固定在墙上；②在A、B两地之间架设电线时，总是尽可能沿线段AB架设；③植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上；④把弯曲的公路改直，就能缩短路程.
A、①② B、①③ C、②④ D、③④7. 如图，在三角形ABC中，线段AB+AC>BC，其理由是（ ）
A、两点确定一条直线 B、两点之间线段最短 C、垂线段最短 D、同一平面内，过一点有且只有一条直线垂直于已知直线8. 如图所示，直线MN表示一条铁路，铁路两旁各有一点A和B，表示两个工厂，要在铁路上建一货站P，使它到两厂距离之和最短，这个货站P应建在AB与MN的交点处，这种故法用几何知识解释应是（ ）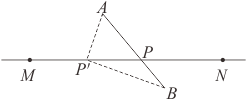
A、两点之间，线段最短 B、射线只有一个端点 C、两直线相交只有一个交点 D、两点确定一条直线二、填空题
-
9. 如图，数轴上A、B两点所表示的数分别为和 ， C是线段的中点，D是数轴上一点，且 ， 则点D表示的数为.
10. 在数轴上，到原点的距离等于3的点所表示的数是.11. 金秋十月，不仅是丰收的季节，而且到处是色彩斑斓的景色，太原市迎泽公园藏着银杏叶极致的风景．小明同学捡到一片沿直线被折断了的银杏叶（如图），他发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是 ．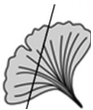
12. 要在墙上订牢一根木条，至少需要2颗钉子，其理由是 ．13. 如图图中有a条直线，b条射线，c条线段，则a+b－c的值等于 ．
三、解答题
-
14. 如图，在一条不完整的数轴上从左到右有点 ， ， ， 其中 ， ， 设点 ， ， 所对应数的和是.若以为原点，求出点 ， 所对应的数，并计算的值；若以为原点，又是多少？
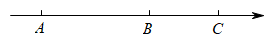15. 如图，已知线段a，b，用尺规作一条线段 ， 使 ．
四、作图题
-
16. 如图，已知线段 ， ， 利用尺规作图法求作线段 ， 使得.（不写作法，保留作图痕迹）
五、综合题
