2023-2024学年初中数学七年级上册 3.4 一元一次方程模型的应用 同步分层训练培优卷(湘教版)
试卷更新日期：2023-09-10 类型：同步测试
一、选择题
-
1. 《九章算术》是中国古代重要的数学著作，其中“盈不足术”记载：今有共买鸡，人出九，盈十一；人出六，不足十六．问人数鸡价各几何？译文：今有人合伙买鸡，每人出9钱，会多出11钱；每人出6钱，又差16钱．问人数、买鸡的钱数各是多少？设人数为x，可列方程为（ ）A、 B、 C、 D、2. 如图是一块在电脑屏幕上出现的长方形色块图，由 6 个不同颜色的正方形组成，已知中间最小的一个正方形的边长为 1，那么这个长方形色块图的周长为（ ）
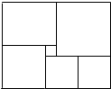A、42 B、48 C、44 D、503. 一家商店将某种服饰按成本价提高40%后标价，又以8折（即按标价80%）优惠卖出，结果每件服饰仍可获利15元，则这种服饰的成本价是（ ）A、125元 B、115元 C、105元 D、95元4. 甲、乙两人从A地出发前往B地，其中甲先出发1 h.如图是甲、乙行驶路（单位：km），（单位：km）随甲行驶时间x（单位：h）变化的图象.当乙追上甲时，乙行驶的时间是（ ）
A、2 h B、3 h C、2.5 h D、3.5 h5. 幻方的历史很悠久，传说最早出现在夏禹时代的“洛书”．把洛书用今天的数学符号翻译出来，就是一个三阶幻方（如图1），将9个数填在3×3（三行三列）的方格中，如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等，就得到一个广义的三阶幻方．图2的方格中填写了一些数字和字母，若能构成一个广义的三阶幻方，则（ ）
A、1 B、2 C、3 D、06. 如图，点A在数轴上表示的数是-8，点B在数轴上表示的数是16．若点A以6个单位长度/秒的速度向右匀速运动，同时点B以2个单位长度/秒的速度向左匀速运动．问：当AB＝8时，运动时间为多少秒？（ ）
A、2秒 B、13.4秒 C、2秒或4秒 D、2秒或6秒7. 如图，现有3×3的方格，每个小方格内均有数字，要求方格内每一行每一列以及每一条对角线上的三个数字之和均相等，记三个数字之和为P，则P的值为（ ）
A、21 B、24 C、27 D、368. 一段跑道长100米，两端分别记为点A、B．甲、乙两人分别从A、B两端同时出发，在这段跑道上来回练习跑步，甲跑步的速度是6m/s，乙跑步的速度为4m/s，练习了足够长时间，他们经过了多次相遇，相遇点离A端不可能是（ ）A、60米 B、0米 C、20米 D、100米二、填空题
-
9. 两个完全相同的长方形按如图方式摆放成“L”形，则该图形的周长为 ．
10. 小伟用撬棍撬动一块大石头，已知阻力和阻力臂分别为1000N和0.6m，当动力臂由1.5m增加到2m时，撬动这块石头可以节省N的力．（杜杆原理：阻力阻力臂动力动力臂）11. 古代中国的数学专著《九章算术》中有一题：“今有生丝三十斤，千之，耗三斤十二两．今有干丝一十二斤，问生丝几何？“意思是：“今有生丝30斤，干燥后耗损3斤12两(古代中国1斤等于16两)．今有干丝12斤，问原有生丝多少？”则原有生丝为斤．12. 某商品随季节变化降价出售，如果按标价降价10%，仍可盈利40元．如果降价后再九折出售，就要亏损14元，则这件商品的标价是 元．13. 如图1是卷筒纸，如图2是它的轴截面的示意图，将厚度为0.02cm的卷筒纸卷在直径为10cm的圆筒上，卷成的卷纸直径为20cm.
(1)、求卷纸围成的轴截面积.(2)、求这卷卷筒纸的总长度 .（取3.14）三、解答题
-
14. 由甲地到乙地前三分之二的路是高速公路，后三分之一的路是普通公路，高速公路和普通公路交界处是丙地．车在高速公路上的行驶速度是 ， 在普通公路上的行驶速度是；车在高速公路上的行驶速度是 ， 在普通公路上的行驶速度是 ， ， 两车分别从甲，乙两地同时出发相向行驶．在高速公路上距离丙地处相遇，求甲，乙两地之间的距离是多少？15. 将一个三位数分成4个数，使得第一个数乘以2，第二个数除以2，第三个数减1，第四个数加2，得到的结果相等，若该三位数比这四个数中最大的数的2倍大59，求这三位数.
四、综合题
-
16. 为了丰富学生的生活，拓宽学生的视野，提高学生各方面的能力，某校组织八年级全体学生共540人前往某社会实践基地开展研学活动，学校若租用8辆A型客车和4辆B型客车，则恰好全部坐满，已知每辆A型客车的乘客座位数比B型客车多12个．(1)、求每辆A型客车和每辆B型客车的乘客座位数．(2)、为确保研学活动能够更好地展开与记录，每辆车上需有1名教师同行，学校决定调整租车方案．已知租用一辆A型客车的费用为2100元，租用一辆B型客车的费用为1500元．在保持租用车辆总数不变的情况下，为接载所有参加活动的师生，如何租用车辆可使得租车总费用最少，并求租车总费用的最小值．17. 如图，A、B两点在一数轴上，其中点O为原点，点A对应的有理数为 ， 点B对应的有理数为20．点A以每秒2个单位长度的速度沿数轴向右运动，设运动时间为t秒 ．
(1)、当时，点A表示的有理数为 ， A、B两点的距离为；(2)、若点B同时以每秒2个单位长度的速度向左运动，经过几秒，点A与点B相遇；(3)、在（2）的条件下，点M（M点在原点）同时以每秒4个单位长度的速度向右运动，几秒后？