2023-2024学年初中数学七年级上册 2.5 整式的加法和减法同步分层训练培优卷(湘教版)

试卷更新日期：2023-09-10 类型：同步测试

进入出卷网下载

一、选择题

1. 数经历了从自然数到有理数，到实数，再到复数的发展过程，数学中把形如 $a + b i (a ， b$ 为实数 $)$ 的数叫做复数，用 $z = a + b i$ 表示，任何一个复数 $z = a + b i$ 在平面直角坐标系中都可以用有序数对 $Z (a ， b)$ 表示，如： $z = 1 + 2 i$ 表示为 $Z (1 ， 2)$ ，则 $z = 2 - i$ 可表示为（）

A、 $Z (2 ， 0)$ B、 $Z (2 ， - 1)$ C、 $Z (2 ， 1)$ D、 $(- 1 ， 2)$

查看试题解析
2. 如果一个正整数可以表示为两个连续奇数的平方差，那么称该正整数为“和谐数”如（ $8 = 3^{2} - 1^{2}$ ， $16 = 5^{2} - 3^{2}$ ，即8，16均为“和谐数”），在不超过2023的正整数中，所有的“和谐数”之和为（　　）

A、255054 B、255064 C、250554 D、255024

查看试题解析
3. 我国在清朝时期的课本中用“ $\frac{五}{丁^{二}} T \frac{三}{丙^{二}} ⊥ \frac{二七}{甲^{二} 乙^{二}}$ ”来表示代数式 $\frac{d^{2}}{5} - \frac{c^{2}}{3} + \frac{a^{2} b^{2}}{27}$ ，那么“ $\frac{五}{甲^{三} 乙^{二}} ⊥ \frac{三}{甲^{三} 乙^{二}}$ ”的化简结果是（）

A、 $\frac{8}{15} a^{3} b^{2}$ B、 $\frac{2}{15} a^{3} b^{2}$ C、 $\frac{8}{a^{3} b^{2}}$ D、 $\frac{2}{a^{3} b^{2}}$

查看试题解析
4. 设 $M = 2 a^{2} + 2 a + 1$ ， $N = 3 a^{2} - 2 a + 7$ ，其中a为实数，则M与N的大小关系是（）

A、 $M \geq N$ B、 $M > N$ C、 $N \geq M$ D、 $N > M$

查看试题解析
5. 数学中余弦定理是这样描述的：在 $△ A B C$ 中， $∠ A$ 、 $∠ B$ 、 $∠ C$ 所对的边分别为 $a$ 、 $b$ 、 $c$ ，则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的2倍，用公式可描述为： $a^{2} = b^{2} + c^{2} - 2 b c c o s A$ ， $b^{2} = a^{2} + c^{2} - 2 a c c o s B$ ， $c^{2} = a^{2} + b^{2} - 2 a b c o s C$ ．在 $△ A B C$ 中， $A B = 3$ ， $A C = 4$ ， $∠ A = 60 °$ ，则 $B C$ 的值是（）

A、5 B、 $\sqrt{14}$ C、 $\sqrt{13}$ D、2

查看试题解析
6. 有自左向右依次排列的三个整式， $a$ ， $a - 3$ ， $- 3$ ，将任意相邻的两个整式相加，所得之和等于在两个整式中间，可以产生一个整式串； $a$ ， $2 a - 3$ ， $a - 3$ ， $a - 6$ ， $- 3$ ，这称为第1次“加法操作”；将第1次“加法操作”后的整式串按上述方法再做一次“加法操作”，可以得到第2次“加法操作”后的整式串；…，以此类推，下列说法：
①当 $3 < a < 6$ 时，第1次“加法操作”后，整式串中所有整式的积为负数；
②第 $n$ 次“加法操作”后，整式串中倒数第二个整式为 $a - 3 - 3 n$ ；
③第4次“加法操作”后，整式串中所有整式之和为 $121 a - 363$ ．
其中正确的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
7. $[x]$ 表示不超过 $x$ 的最大整数．如 $[π] = 3$ ， $[2] = 2$ ， $[- 2.1] = - 3$ ．则下列结论：① $[- x] = - [x]$ ；②若 $[x] = n$ ，则 $x$ 的取值范围是 $n \leq x < n + 1$ ；③当 $- 1 < x < 1$ 时， $[1 + x] + [1 - x]$ 的值为1或2；④ $x = - 2.75$ 是方程 $4 x - 2 [x] + 5 = 0$ 的唯一一个解．其中正确的结论是（）

A、①② B、②④ C、②③ D、①③

查看试题解析
8. 有n个依次排列的整式：第一项是a² ，第二项是a²+2a+1，用第二项减去第一项，所得之差记为b₁ ，将b₁加2记为b₂ ，将第二项与b₂相加作为第三项，将b₂加2记为b₃ ，将第三项与b₃相加作为第四项，以此类推；某数学兴趣小组对此展开研究，得到4个结论：
①b₃＝2a+5；
②当a＝2时，第3项为16；
③若第4项与第5项之和为25，则a＝7；
④第2022项为（a+2022）²；
⑤当n＝k时，b₁+b₂+…+bk＝2ak+k²；
以上结论正确的是（）

A、①②⑤ B、①③⑤ C、①②④ D、②④⑤

查看试题解析

二、填空题

9. 定义：两正数 $a$ ， $b$ 之间的一种运算，记作 $(a ， b)$ ；若 $a^{c} = b$ ，则 $(a ， b) = c$ ．例如：因为 $3^{2} = 9$ ，所以 $(3 ， 9) = 2$ ．

(1)、根据上述规定，填空： $(5 ， 1)$ ＝；

(2)、小明在研究这种运算时发现一个现象： $(2^{n} ， 3^{n}) = (2 ， 3)$ ．
小明给出了如下的证明：设 $(2^{n} ， 3^{n}) = x$ ，则根据定义，得 ${(2^{n})}^{x} = 3^{n}$ ，即 ${(2^{x})}^{n} = 3^{n}$ 所以 $2^{x} = 3$ ，即 $(2 ， 3) = x$ ，所以 $(2^{n} ， 3^{n}) = (2 ， 3)$ ．
请你尝试运用这种方法解决问题：已知a、m、n均为正数，填空： $(a ， m) + (a ， n) =$ $(a ，$ $)$

查看试题解析
10. 如图长方形 $A B C D$ 由图1、2、3、4、5拼成，设图1、2、3是边长分别为a，b，c $(a < b < c)$ 的正方形，图4是长方形，图5是正方形．对于判断：① $a + b > c$ ；②图4的周长为 $3 b + c$ ；③ $a + c = 2 b$ ；④长方形 $A B C D$ 的周长为 $2 (a + b + c)$ ，其中正确的是（填编号）．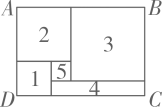

查看试题解析
11. 对于任意实数a，b，c，d，我们规定： $| a b | = a x + b y$ ，根据这一规定，若x，y同时满足 $| 1 - 1 | = - 1 ， | 2 1 ∣ = - 8$ ，则 $| - 1 3 |$ 的值是.

查看试题解析
12. 对实数 $a$ 、 $b$ ，定义运算☆如下： $a$ ☆ $b =$ ${\begin{array}{l} a^{b} (a ＞ b ， a \neq 0 ） \\ a^{- b} (a \leq b ， a \neq 0 ）， \end{array}$ ，
例如2☆3= $2^{- 3} = \frac{1}{8}$ .计算[2☆( $- 4$ )] $\times$ [( $- 4$ )☆( $- 2$ )]=

查看试题解析
13. 对于一个三位正整数 $Q = \bar{a b c}$ ，若各个数位上的数字都不为 $0$ ，且百位数字与个位数字之和恰好等于十位数字的两倍，则称这个三位正整数 $Q$ 叫“中项两倍数” $.$ 把“中项两倍数” $Q$ 的各个数字之和被 $3$ 整除的商记为 $F (Q) .$ 其中，能被 $21$ 整除，且 $\sqrt{F (Q)}$ 为有理数的所有“中项两倍数” $Q$ 的值为．

查看试题解析

三、解答题

14. 我们规定 $| \begin{array}{l} a & b \\ c & d \end{array} |$ 的运算法则为 $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ ，例如 $| \begin{array}{l} 5 & 3 \\ 4 & 6 \end{array} | = 5 \times 6 - 3 \times 4 = 18$ . 若 $| \begin{array}{l} 6 & 4 - x \\ 2 & x \end{array} | > 0$ ，求 $x$ 的取值范围.

查看试题解析
15. 老师在黑板上写了一个正确的演算过程，随后用手捂住了其中一个多项式，形式如下： $- (a^{2} b - 2 a b^{2}) + a b^{2} = 2 (a^{2} b + a b^{2})$ 试问：老师用手捂住的多项式是什么?

查看试题解析

四、综合题

16.

(1)、填空：
$2^{1} - 2^{0} = 2^{()}$

$2^{2} - 2^{1} = 2^{()}$

$2^{3} - 2^{2} = 2^{()}$

$⋮$

(2)、探索（1）中式子的规律，试写出第 $n$ 个等式，并说明第 $n$ 个等式成立；

(3)、计算 $2^{0} + 2^{1} + 2^{2} + \cdot \cdot \cdot + 2^{2023}$ ．

查看试题解析
17. 规定两数a，b之间的一种运算，记作(a，b)：如果a^c＝b，那么(a，b)＝c.例如：∵2³＝8，∴(2，8)＝3.

(1)、根据上述规定，填空：(3，27)＝， (5，1)＝， $(\begin{array}{l} 2 ， \frac{1}{4} \end{array})$ ＝；

(2)、小明在研究这种运算时发现一个现象：(3ⁿ ， 4ⁿ)＝(3，4)，小明给出了如下的理由：
设(3ⁿ ， 4ⁿ)＝x，则(3ⁿ)^x＝4ⁿ ，即(3^x)ⁿ＝4ⁿ ，

∴3^x＝4，即(3，4)＝x，

∴(3ⁿ ， 4ⁿ)＝(3，4)．

请你尝试运用这种方法判断(3，4)＋(3，5)＝(3，20)是否成立，若成立，请说明理由．

查看试题解析

2023-2024学年初中数学七年级上册 2.5 整式的加法和减法 同步分层训练培优卷(湘教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学七年级上册 2.5 整式的加法和减法同步分层训练培优卷(湘教版)