2023-2024学年高中数学人教A版选修二 5.1 导数的概念及其意义同步练习

试卷更新日期：2023-09-10 类型：同步测试

进入出卷网下载

一、选择题

1. 若曲线 $y = x^{2} - l n x$ 的一条切线的斜率是 $- 1$ ，则切点的横坐标为（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $e$

查看试题解析
2. 某物体的运动路程 $s ($ 单位： $m)$ 与时间 $t ($ 单位： $s)$ 的关系可用函数 $s (t) = t^{2} + 3$ 表示，则该物体在 $t = 2 s$ 时的瞬时速度为（）

A、 $0 m / s$ B、 $2 m / s$ C、 $3 m / s$ D、 $4 m / s$

查看试题解析
3. 已知某质点运动的位移 $y$ （单位； $c m$ ）与时间 $t$ （单位； $s$ ）之间的关系为 $y (t) = l n (2 t + 1)$ ，则该质点在 $t = 2 s$ 时的瞬时速度为（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、2 D、4

查看试题解析
4. 若函数 $f (x) = x l n x$ 在点 $(x_{0} ， f (x_{0}))$ 处的切线斜率为1，则 $x_{0} =$ （）

A、-e B、e C、-1 D、1

查看试题解析
5. 若存在直线 $y = k x + b$ ，使得函数 $F (x)$ 和 $G (x)$ 对其公共定义域上的任意实数 $x$ 都满足 $F (x) \geq k x + b \geq G (x)$ ，则称此直线 $y = k x + b$ 为 $F (x)$ 和 $G (x)$ 的“隔离直线”.已知函数 $f (x) = x^{2}$ ， $g (x) = a l n x (a > 0)$ ，若 $f (x)$ 和 $g (x)$ 存在唯一的“隔离直线”，则 $a =$ （）

A、 $\sqrt{e}$ B、 $2 \sqrt{e}$ C、 $e$ D、 $2 e$

查看试题解析
6. 已知物体的位移 $S$ （单位：m）与时间 $t$ （单位：s）满足函数关系 $S = 2 s i n (π t)$ ，则物体在 $t = 2$ 时的瞬时速度为（）

A、 $2 π (m / s)$ B、 $- 2 π (m / s)$ C、 $2 (m / s)$ D、 $- 2 (m / s)$

查看试题解析
7. 已知函数 $y = f (x)$ 的图象如图所示，设函数 $y = f (x)$ 从 $- 1$ 到 $1$ 的平均变化率为 $v_{1}$ ，从 $1$ 到 $2$ 的平均变化率为 $v_{2}$ ，则 $v_{1}$ 与 $v_{2}$ 的大小关系为（）

A、 $v_{1} > v_{2}$ B、 $v_{1} = v_{2}$ C、 $v_{1} < v_{2}$ D、不确定

查看试题解析
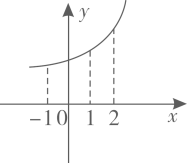8. 若经过点P(2，8)作曲线 $y = x^{3}$ 的切线，则切线方程为（）

A、 $12 x - y - 16 = 0$ B、 $3 x - y + 2 = 0$ C、 $12 x - y + 16 = 0$ 或 $3 x - y - 2 = 0$ D、 $12 x - y - 16 = 0$ 或 $3 x - y + 2 = 0$

查看试题解析

二、多项选择题

9. 在曲线 $y = s i n 2 x$ 上的切线的倾斜角为 $\frac{π}{3}$ 点的横坐标可能为（）

A、 $- \frac{π}{12}$ B、 $\frac{π}{6}$ C、 $\frac{π}{3}$ D、 $\frac{π}{12}$

查看试题解析
10. 形如 $f (x) = a x + \frac{b}{x} (a > 0 ， b > 0)$ 的函数是我们在中学阶段最常见的一个函数模型，因其形状像极了老师给我们批阅作业所用的“√”，所以也称为“对勾函数”．研究证明，对勾函数可以看作是焦点在坐标轴上的双曲线绕原点旋转得到，即对勾函数是双曲线．已知 $O$ 为坐标原点，下列关于函数 $f (x) = x + \frac{1}{x}$ 的说法正确的是（）

A、渐近线方程为 $x = 0$ 和 $y = x$ B、 $y = f (x)$ 的对称轴方程为 $y = (\sqrt{2} + 1) x$ 和 $y = (1 - \sqrt{2}) x$ C、 $M ， N$ 是函数 $f (x)$ 图象上两动点， $P$ 为 $M N$ 的中点，则直线 $M N ， O P$ 的斜率之积为定值 D、 $Q$ 是函数 $f (x)$ 图象上任意一点，过点 $Q$ 作切线，交渐近线于 $A ， B$ 两点，则 $△ O A B$ 的面积为定值

查看试题解析

三、填空题

11. 曲线 $y = e^{x} c o s x$ 在 $x = 0$ 处的切线方程为.

查看试题解析
12. 已知函数 $f (x) = x^{3} - 2 l n x$ ，那么 $f (x)$ 在点 $(1 ， f (1))$ 处的切线方程为．

查看试题解析
13. 函数 $f (x) = c o s x - s i n x$ 的图象在点 $(\frac{π}{2} ， f (\frac{π}{2}))$ 处的切线方程为．

查看试题解析
14. 曲线 $f (x) = (3 x + 2) l n x + 1$ 在点 $(1 ， f (1))$ 处的切线方程为．

查看试题解析
15. 过点 $(0 ， 1)$ 的直线 $l$ 与圆 $x^{2} + y^{2} + 4 x + 3 = 0$ 相切，则直线 $l$ 的斜率为.

查看试题解析
16. 曲率是衡量曲线弯曲程度的重要指标 $.$ 定义：若 $f' (x)$ 是 $f (x)$ 的导函数， $f$ 是 $f' (x)$ 的导函数，则曲线 $y = f (x)$ 在点 $(x ， f (x))$ 处的曲率 $K = \frac{| f'' (x) |}{[1 + (f^{'} (x))^{2}]^{2}} .$ 已知 $f (x) = c o s (x - 1) - l n x$ ，则曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的曲率为．

查看试题解析
17. 已知函数 $f (x) = s i n 2 x - c o s 2 x$ ，曲线 $y = f (x)$ 在点 $(x_{0} ， f (x_{0}))$ 处的切线与直线 $\frac{1}{2} x + \sqrt{2} y = 0$ 垂直，则 $t a n x_{0} =$ ．

查看试题解析
18. 已知曲线 $C_{1}$ ： $y = x^{2} + a x - 2 a^{2}$ 在 $x = t$ 处的切线为 $l_{1}$ ，曲线 $C_{2}$ ： $y = l n x$ 在 $x = t$ 处的切线为 $l_{2}$ ，若存在实数t使得 $l_{1}$ 与 $l_{2}$ 的倾斜角互补，则实数a的取值范围为．

查看试题解析

2023-2024学年高中数学人教A版选修二 5.1 导数的概念及其意义 同步练习

一、选择题

二、多项选择题

三、填空题

2023-2024学年高中数学人教A版选修二 5.1 导数的概念及其意义同步练习