2023-2024学年高中数学人教A版选修二 4.1 数列的概念同步练习

试卷更新日期：2023-09-10 类型：同步测试

进入出卷网下载

一、选择题

1. 数列 $- 3 ， \frac{5}{4} ， - \frac{7}{9} ， \frac{9}{16} ， ⋯$ 的第11项是（）

A、 $- \frac{23}{121}$ B、 $\frac{23}{121}$ C、 $- \frac{21}{121}$ D、 $\frac{21}{121}$

查看试题解析
2. 若数列 ${a_{n}}$ 满足 $a_{n + 1} = \frac{1}{1 - a_{n}}$ ， $a_{1} = 2$ ，则 $a_{2023} =$ （）

A、 $- 1$ B、 $1$ C、 $2$ D、 $\frac{1}{2}$

查看试题解析
3. 数列 ${(- 1)^{n} c o s \frac{n π}{4}}$ 的第5项为（　　）

A、0 B、 $- 1$ C、 $\frac{\sqrt{2}}{2}$ D、 $- \frac{\sqrt{2}}{2}$

查看试题解析
4. 已知数列 ${a_{n}}$ 的通项公式是 $a_{n} = n^{2} + 2 n$ ，则下列各数是 ${a_{n}}$ 中的项的是（）

A、10 B、18 C、26 D、63

查看试题解析
5. 斐波那契数列 ${a_{n}}$ 满足 $a_{1} = a_{2} = 1 ， a_{n} = a_{n - 1} + a_{n - 2} (n \geq 3)$ ，其每一项称为“斐波那契数”.如图，在以斐波那契数为边长的正方形拼成的长方形中，利用下列各图中的面积关系，推出 $\frac{a_{1}^{2} + a_{2}^{2} + ⋯ + a_{2023}^{2}}{a_{2023}}$ 是斐波那契数列的第（）项.

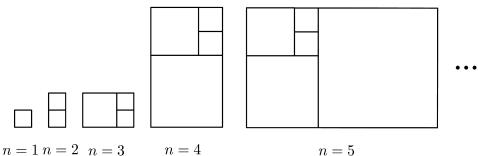A、2022 B、2023 C、2024 D、2025

查看试题解析
6. 在数列 ${b_{n}}$ 中，若有 $b_{m} = b_{n}$ （ $m$ ， $n$ 均为正整数，且 $m \neq n$ ），就有 $b_{m + 1} = b_{n + 1}$ ，则称数列 ${b_{n}}$ 为“递等数列”.已知数列 ${a_{n}}$ 满足 $a_{5} = 5$ ，且 $a_{n} = n (a_{n + 1} - a_{n})$ ，将“递等数列” ${b_{n}}$ 前 $n$ 项和记为 $S_{n}$ ，若 $b_{1} = a_{1} = b_{4}$ ， $b_{2} = a_{2}$ ， $S_{5} = a_{10}$ ，则 $S_{2023} =$ （）

A、4720 B、4719 C、4718 D、4716

查看试题解析

二、多项选择题

7. 下列是递增数列的是（）

A、 ${2 n + 1}$ B、 ${2^{2 n} - 2^{n + 3}}$ C、 ${2^{n} - n}$ D、 ${(- 2)^{n}}$

查看试题解析
8. 在数列 ${a_{n}}$ 中，若对于任意 $n \in N^{*}$ ，都有 $a_{n + 1} + \frac{6}{a_{n} + 1} = 4$ ，则（）

A、当 $a_{1} = 1$ 或 $a_{1} = 2$ 时，数列 ${a_{n}}$ 为常数列 B、当 $a_{1} > 2$ 时，数列 ${a_{n}}$ 为递减数列，且 $2 < a_{n} \leq a_{1}$ C、当 $1 < a_{1} < 2$ 时，数列 ${a_{n}}$ 为递增数列 D、当 $0 < a_{1} < 1$ 时，数列 ${a_{n}}$ 为单调数列

查看试题解析
9. 已知数列 ${a_{n}}$ 满足 $a_{1} = 8$ ， $a_{2} = 1$ ， $a_{n + 2} = {\begin{array}{l} - a_{n} ， n 为偶数 \\ a_{n} - 2 ， n 为奇数 \end{array}$ ， $T_{n}$ 为数列 ${a_{n}}$ 的前n项和，则下列说法正确的有（）

A、n为偶数时， $a_{n} = {(- 1)}^{\frac{n - 2}{2}}$ B、 $T_{2 n} = - n^{2} + 9 n$ C、 $T_{99} = - 2049$ D、 $T_{n}$ 的最大值为20

查看试题解析
10. 已知数列 ${a_{n}}$ ， $a_{2} = \frac{1}{2}$ ，且满足 $a_{n + 1} a_{n}^{2} = a_{n} - a_{n + 1}$ ， $n \in N^{*}$ ，则（）

A、 $a_{4} - a_{1} = \frac{19}{29}$ B、 $a_{n}$ 的最大值为 $1$ C、 $a_{n + 1} \geq \frac{1}{n + 1}$ D、 $\sqrt{a_{1}} + \sqrt{a_{2}} + \sqrt{a_{3}} + \cdot \cdot \cdot + \sqrt{a_{35}} > 10$

查看试题解析

三、填空题

11. 已知数列 ${a_{n}}$ 满足 $a_{1} = 0 ， a_{2} = a_{3} = 2 ， a_{n} \neq - 1$ ，且 $a_{n} a_{n + 3} + a_{n} + a_{n + 3} = 1$ ，若 $b_{n} = [\frac{3}{2} a_{n}]$ （其中 $[\frac{3}{2} a_{n}]$ 表示不超过 $\frac{3}{2} a_{n}$ 的最大整数），则 $a_{5} =$ ；数列 ${b_{n}}$ 前2023项和 $S_{2023} =$ ．

查看试题解析
12. 若项数为10的数列 ${a_{n}}$ ，满足 $1 \leq | a_{i + 1} - a_{i} | \leq 2 (i = 1 ， 2 ， \dots ， 9)$ ，且 $a_{1} = a_{10} \in [- 1 ， 0]$ ，则数列 ${a_{n}}$ 中最大项的最大值为.

查看试题解析
13. 某工厂去年12月试产1050个高新电子产品，产品合格率为90％.从今年1月开始，工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产，以后每月的产量都在前一个月的基础上提高5％，产品合格率比前一个月增加0.4％.设从今年1月起（作为第一个月），第个月，月不合格品数量首次控制在100个以内.
（参考数据： $1.0 5^{10} \approx 1.6$ ， $1.0 5^{11} \approx 1.7$ ， $1.0 5^{12} \approx 1.8$ ， $1.0 5^{13} \approx 1.9$ ）

查看试题解析
14. 若数列 ${a_{n}}$ 满足 $a_{n + 1} > a_{n}$ 且 $S_{n + 1} < S_{n}$ ，其中 $S_{n}$ 为数列 ${a_{n}}$ 的前n项和．请写出一个满足上述条件的数列通项 $a_{n} =$ ．

查看试题解析

四、解答题

15. 记 $S_{n}$ 为数列 ${a_{n}}$ 的前 $n$ 项和，已知 $a_{1} = 2 ， 2 S_{n} = n a_{n + 1}$ ．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = \frac{1}{a_{n} \cdot a_{n + 1}}$ ，记数列 ${b_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，证明： $T_{n} < \frac{1}{4}$ ．

查看试题解析
16. 数列 ${a_{n}}$ ， ${b_{n}}$ 满足 ${\begin{array}{l} a_{n + 1} = \frac{1}{2} a_{n} + \frac{1}{2} b_{n} \\ \frac{1}{b_{n + 1}} = \frac{1}{2} \cdot \frac{1}{a_{n}} + \frac{1}{2} \cdot \frac{1}{b_{n}} \end{array}$ ， $a_{1} > 0$ ， $b_{1} > 0$ ．

(1)、求证： ${a_{n} \cdot b_{n}}$ 是常数列；

(2)、设 $a_{1} = 4$ ， $b_{1} = 1$ ，求 $a_{n}$ 的最大项．

查看试题解析
17. 已知数列 ${a_{n}}$ 满足 $a_{n + 1} - a_{n} = 2^{n}$ ，且 $a_{1} = 1$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = \frac{a_{n} + 1}{a_{n} a_{n + 1}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
18. 已知数列 ${a_{n}}$ 满足 $\sqrt{a_{1}} + \sqrt{a_{2}} + ⋯ + \sqrt{a_{n}} = \frac{n^{2} + n + 2}{2}$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、记 $b_{n} = \frac{1}{a_{n} + \sqrt{a_{n}}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析
19. 已知数列 ${a_{n}}$ 满足 $a_{1} + 3 a_{2} + ⋯ + (2 n - 1) a_{n} = n$ .

(1)、求 ${a_{n}}$ 的通项公式；

(2)、已知 $c_{n} = {\begin{array}{l} \frac{1}{19 a_{n}} ， n 为奇数， \\ a_{n} a_{n + 2} ， n 为偶数， \end{array}$ 数列 ${c_{n}}$ 的前20项和.

查看试题解析
20. 在数列 ${a_{n}}$ 中， $a_{1} = 3 ， a_{n + 1} - a_{n} = 2 n + 3$ .

(1)、求 $a_{n}$ ；

(2)、设 $b_{n} = \frac{n}{(n + 1) a_{n}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析

2023-2024学年高中数学人教A版选修二 4.1 数列的概念 同步练习

一、选择题

二、多项选择题

三、填空题

四、解答题

2023-2024学年高中数学人教A版选修二 4.1 数列的概念同步练习