2023-2024学年高中数学人教A版必修一5.7 三角函数的应用同步练习

试卷更新日期：2023-09-10 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，某摩天轮最高点距离地面高度为 $120$ $m$ ，转盘直径为 $110 m$ ，开启后按逆时针方向匀速旋转，旋转一周需要 $30$ $m i n$ .游客在座舱转到距离地面最近的位置进舱，开始转动 $t$ $m i n$ 后距离地面的高度为 $H$ $m$ ，则在转动一周的过程中，高度 $H$ 关于时间 $t$ 的函数解析式是（）

A、 $H = 55 c o s (\frac{π}{15} t - \frac{π}{2}) + 65 (0 \leq t \leq 30)$ B、 $H = 55 s i n (\frac{π}{15} t - \frac{π}{2}) + 65 (0 \leq t \leq 30)$ C、 $H = - 55 c o s (\frac{π}{10} t + \frac{π}{2}) + 65 (0 \leq t \leq 30)$ D、 $H = - 55 s i n (\frac{π}{10} t + \frac{π}{2}) + 65 (0 \leq t \leq 30)$

查看试题解析
2. 智能主动降噪耳机工作的原理是通过耳机两端的噪声采集器采集周围的噪声，然后通过主动降噪芯片生成的声波来抵消噪声（如图）．已知噪声的声波曲线是 $y = 2 c o s 3 x$ ，通过主动降噪芯片生成的声波曲线是 $y = A s i n (ω x + φ)$ （其中 $A > 0 ， ω > 0 ， 0 \leq φ < 2 π$ ），则 $φ =$ （）

A、 $\frac{π}{2}$ B、π C、 $\frac{3 π}{2}$ D、 $\frac{π}{6}$

查看试题解析
3. 2022年春节期间，G市某天从8~16时的温度变化曲线（如图）近似满足函数 $f (x) = 2 \sqrt{2} c o s (ω x + φ)$ （ $ω > 0$ ， $0 < φ < π$ ， $x \in [8 ， 16]$ ）的图像．下列说法正确的是（）

A、8～13时这段时间温度逐渐升高 B、8～16时最大温差不超过5℃ C、8～16时0℃以下的时长恰为3小时 D、16时温度为−2℃

查看试题解析
4. 摩天轮常被当作一个城市的地标性建筑，如静安大悦城的“Sky Ring”摩天轮是上海首个悬臂式屋顶摩天轮.摩天轮最高点离地面高度106米，转盘直径56米，轮上设置30个极具时尚感的4人轿舱，拥有360度的绝佳视野.游客从离楼顶屋面最近的平台位置进入轿舱，开启后按逆时针匀速旋转t分钟后，游客距离地面的高度为h米， $h = - 28 c o s (\frac{π t}{6}) + 78$ .若在 $t_{1}$ ， $t_{2}$ 时刻，游客距离地面的高度相等，则 $t_{1} + t_{2}$ 的最小值为（　　）

A、6 B、12 C、18 D、24

查看试题解析
5. 红河州个旧市是一个风景优美的宜居城市，如图是个旧宝华公园的摩天轮，半径为20米，圆心O距地面的高度为25米，摩天轮运行时按逆时针匀速旋转，转一周需要10分钟.摩天轮上的点P的起始位置在最低点处.若游客在距离地面至少35米的高度能够将个旧市区美景尽收眼底，则摩天轮转动一周内具有最佳视觉效果的时间长度（单位：分钟）为（）

A、 $\frac{8}{3}$ B、3 C、 $\frac{10}{3}$ D、 $\frac{11}{3}$

查看试题解析
6. 筒车是我们古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理，如图所示，已知筒车的半径为 $4 m$ ，筒车转轮的中心 $O$ 到水面的距离为 $2 m$ ，筒车沿逆时针方向以角速度 $ω (ω > 0)$ 转动，规定：盛水筒 $M$ 对应的点 $P$ 从水中浮现（即 $P_{0}$ 时的位置）时开始计算时间，且以水轮的圆心 $O$ 为坐标原点，过点 $O$ 的水平直线为 $x$ 轴建立平面直角坐标系 $x O y$ ，设盛水筒 $M$ 从点 $P_{0}$ 运动到点 $P$ 时经过的时间为 $t$ （单位： $s$ ），且此时点 $P$ 距离水面的高度为 $h$ （单位：米），筒车经过 $6 s$ 第一次到达最高点，则下列叙述正确的是（）

A、当 $t = 16 s$ 时，点 $P$ 与点 $P_{0}$ 重合 B、当 $t \in [51 ， 65]$ 时， $h$ 一直在增大 C、当 $t \in (0 ， 50)$ 时，盛水筒有 $5$ 次经过水平面 D、当 $t = 50$ 时，点 $P$ 在最低点

查看试题解析

二、多项选择题

7. 已知函数 $f (x) = a s i n ω x + c o s ω x (a > 0 ， ω > 0)$ 的部分图象如图所示，其中 $| B C | = 2$ ，且 $△ A B C$ 的面积为 $2$ ，则下列函数值恰好等于 $a$ 的是（）

A、 $f (\frac{1}{3})$ B、 $f (\frac{5}{6})$ C、 $f (1)$ D、 $f (2)$

查看试题解析
8. 质点 $A$ 和 $B$ 在以坐标原点 $O$ 为圆心，半径为1的 $⊙ O$ 上顺时针作匀速圆周运动，同时出发. $A$ 的角速度大小为 $1 r a d / s$ ，起点为 $⊙ O$ 与 $x$ 轴正半轴的交点； $B$ 的角速度为 $4 r a d / s$ ，起点为射线 $y = \frac{\sqrt{3}}{3} x (x \geq 0)$ 与 $⊙ O$ 的交点.则当 $B$ 与 $A$ 重合时， $B$ 的坐标可以为（）

A、 $(c o s \frac{11}{18} π ， s i n \frac{11}{18} π)$ B、 $(- c o s \frac{13}{18} π ， s i n \frac{13}{18} π)$ C、 $(c o s \frac{π}{18} ， - s i n \frac{π}{18})$ D、 $(- c o s \frac{π}{18} ， s i n \frac{π}{18})$

查看试题解析
9. 水车是我国劳动人民创造发明的一种灌溉工具，作为中国农耕文化的组成部分，充分体现了中华民族的创造力，见证了中国农业文明．水车的外形酷似车轮，在轮的边缘装有若干个水斗，借助水势的运动惯性冲动水车缓缓旋转，将水斗内的水逐级提升．某水车轮的半径为5米，圆心距水面的高度为4米，水车按逆时针方向匀速转动，每分钟转动2圈，当其中的一个水斗 $A$ 到达最高点时开始计时，设水车转动 $t$ （分钟）时水斗 $A$ 距离水面的高度（水面以上为正，水面以下为负）为 $f (t)$ （米），下列选项正确的是（）

A、 $f (t) = 5 c o s 4 π t + 4$ （ $t \geq 0$ ） B、 $f (t) = 5 s i n (π t + \frac{π}{2}) + 4$ （ $t \geq 0$ ） C、 $- \frac{1}{2}$ 是函数 $f (t)$ 的周期 D、在旋转一周的过程中，水斗 $A$ 距离水面高度不低于6.5米的时间为10秒．

查看试题解析
10. 潮汐现象是由于海水受日月的引力在一定的时候发生涨落的现象，一般早潮叫潮，晚潮叫汐，在通常情况下，船在涨潮时驶进航道，靠近船坞卸货后落潮时返回海洋，现有一条货船的吃水深度（船底与水面的距离）为 $4 m$ ，根据安全条例规定至少要有 $2 m$ 的安全间隙（船底与海底的距离），已知某港口在某季节的某一天的时刻 $x$ （单位：小时）与水深 $f (x)$ （单位： $m$ ）的关系为： $f (x) = 2 s i n \frac{π}{6} x + 5 (0 \leq x \leq 24)$ ，则下列说法中正确的有（）

A、相邻两次潮水高度最高的时间间距为 $24 h$ B、18时潮水起落的速度为 $- \frac{π}{3} m / h$ C、该货船在2：00至4：00期间可以进港 D、该货船在13：00至17：00期间可以进港

查看试题解析
11. 衢州市柯城区沟溪乡余东村是中国十大美丽乡村，也是重要的研学基地，村口的大水车，是一道独特的风景.假设水轮半径为4米（如图所示），水轮中心O距离水面2米，水轮每60秒按逆时针转动一圈，如果水轮上点P从水中浮现时（图中 $P_{0}$ ）开始计时，则（）

A、点P第一次达到最高点，需要20秒 B、当水轮转动155秒时，点P距离水面2米 C、在水轮转动的一圈内，有15秒的时间，点P距水面超过2米 D、点P距离水面的高度h（米）与t（秒）的函数解析式为 $h = 4 s i n (\frac{π}{30} t - \frac{π}{6}) + 2$

查看试题解析
12. 如图，一圆形摩天轮的直径为100米，圆心O到水平地面的距离为60米，最上端的点记为Q，现在摩天轮开始逆时针方向匀速转动，30分钟转一圈，以摩天轮的中心为原点建立平面直角坐标系，则下列说法正确的是（）

A、点Q距离水平地面的高度与时间的函数为 $h (t) = 50 s i n (\frac{π t}{15} + \frac{π}{3}) + 10$ B、点Q距离水平地面的高度与时间的函数的对称中心坐标为 $(15 k ， 60) (k \in Z)$ C、经过10分钟点Q距离地面35米 D、摩天轮从开始转动一圈，点Q距离水平地面的高度不超过85米的时间为20分钟

查看试题解析

三、填空题

13. 一个单摆作简谐振动位移-时间图象如图所示，S表示离开O的位移（单位：cm），t表示振动的时间（单位：s），则该简谐振动的振幅为cm，振动的最小正周期为s．

查看试题解析
14. 如图，一个筒车按逆时针方向旋转，每分钟转5圈，若从盛水筒P刚出水面开始计时，则盛水筒到水面的距离y（单位：m）（水面下则y为负数）与时间t（单位：s）之间的关系式为 $y = 4 s i n (ω t + φ) + 2 \sqrt{3} (| φ | < \frac{π}{2})$ ，盛水筒至少经过s能到达距离水面 $4 \sqrt{3} m$ 的位置．

查看试题解析
15. 某城市一年中12个月的平均气温与月份的关系可近似地用三角函数 $y = a + A c o s [\frac{π}{6} (x - 6)]$ （x=1，2，3，…，12）来表示，已知6月份的月平均气温为28℃；12月份的月平均气温为18℃，则10月份的平均气温为℃.

查看试题解析
16. 在平面直角坐标系中，半径为1的圆 $C$ 与 $x$ 轴相切于原点 $O$ ，圆 $C$ 上有一定点 $P$ ，坐标是 $(1 ， 1)$ ．假设圆 $C$ 以 $\frac{π}{5}$ （单位长度）/秒的速度沿 $x$ 轴正方向匀速滚动，那么当圆 $C$ 滚动 $t$ 秒时，点 $P$ 的横坐标 $x =$ ．（用 $t$ 表示）

查看试题解析
17. 摩天轮是一种大型转轮状的机械建筑设施，某摩天轮最高点距离地面高度128米，转盘直径为120米，设置有48个座舱，开启后按逆时针方向匀速旋转，游客在座舱转到距离地面最近的位置进舱，转一周需要30分钟.若游客甲坐上摩天轮的座舱，开始旋转 $t$ 分钟后距离地面的高度为 $h$ 米，则 $h$ 关于 $t$ 的函数解析式为；若游客甲在 $t_{1}$ ， $t_{2}$ 时刻距离地面的高度相等，则 $t_{1} + t_{2}$ 的最小值为.

查看试题解析
18. 摩天轮是一种大型转轮状的机械建筑设施，稳坐于永乐桥之上的“天津之眼”作为世界上唯一一座建在桥上的摩天轮，其巧夺天工和奇思妙想确是当之无愧的“世界第一”.如图，永乐桥摩天轮的直径为 $110 m$ ，到达最高点时，距离地面的高度为 $120 m$ ，能看到方圆 $40 km$ 以内的景致，是名副其实的“天津之眼”.实际上，单从高度角度来看，天津之眼超越了曾大名鼎鼎的伦敦之眼而跃居世界第一.永乐桥摩天轮设置有48个座舱，开启后按逆时针方向匀速旋转，游客在座舱转到距离地面最近的位置进舱，转一周大约需要 $30 \min$ .游客甲坐上摩天轮的座舱，开始转到 $t \min$ 后距离地面的高度为 $H m$ ，则转到 $10 \min$ 后距离地面的高度为 $m$ ，在转动一周的过程中， $H$ 关于 $t$ 的函数解析式为.

查看试题解析

四、解答题

19. 如图，某地一天从4~18时的温度变化曲线近似满足函数 $y = A c o s (ω x + ϕ) + b ， 0 < ϕ < π$ ．

(1)、求A，b， $ω$ ， $ϕ$ ；

(2)、为响应国家节能减排的号召，建议室温室25℃以上才开空调，求在 $[0 ， 24]$ 内，该地适宜开空调的时间段．

查看试题解析
20. 如图，一个直径为 $5 m$ 的水车按逆时针方向每分钟转1.8圈，水车的中心 $O$ 距离水面的高度为 $1.25 m$ ，水车上的盛水筒 $P$ 到水面的距离为 $h$ （单位： $m$ ）（在水面下则 $h$ 为负数），若以盛水筒 $P$ 刚浮出水面时开始计时，则 $h$ 与时间 $t$ （单位： $s$ ）之间的关系为 $h = A s i n (ω t + φ) + b (A > 0 ， ω > 0 ， | φ | < \frac{π}{2})$ .

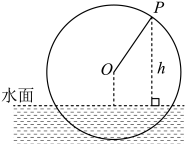(1)、求 $h$ 与 $t$ 的函数解析式；

(2)、求在一个旋转周期内，盛水筒 $P$ 在水面以上的时长.

查看试题解析
21. 某游乐场的摩天轮示意图如图．已知该摩天轮的半径为30米，轮上最低点与地面的距离为2米，沿逆时针方向匀速旋转，旋转一周所需时间为 $T = 24$ 分钟．在圆周上均匀分布12个座舱，标号分别为 $1 ~ 12$ （可视为点），现从图示位置，即1号座舱位于圆周最右端时开始计时，旋转时间为 $t$ 分钟．

(1)、当 $t = 6$ 时，求1号座舱与地面的距离；

(2)、记1号座舱与5号座舱高度之差的绝对值为 $H$ 米，若在 $0 ≤ t ≤ t_{0}$ 这段时间内， $H$ 恰有三次取得最大值，求 $t_{0}$ 的取值范围．

查看试题解析
22. 筒车是我国古代发明的一种灌溉工具，因其经济又环保，至今还在农业生产中得到使用（图1）.如图2，现有一个半径为4米的筒车按逆时针方向每分钟匀速旋转1圈，筒车的轴心 $O$ 距离水面的高度为2米，若以盛水筒 $P$ 刚浮出水面在点 $A$ 处时为初始时刻，设经过 $t$ 秒后盛水筒 $P$ 到水面的距离为 $f (t)$ （单位：米）（在水面下则 $f (t)$ 为负数）.筒车上均匀分布着12个盛水筒，假设盛水筒在最高处时把水倾倒到水槽上.

(1)、求函数 $f (t)$ 的表达式；

(2)、求第一筒水倾倒的时刻 $t$ 和相邻两个盛水筒倾倒的时间差；

(3)、若某一稻田灌溉需水量为100立方米，一个盛水筒倾倒到水槽的水约为0.01立方米，求需要多少小时才能完成该稻田的浇灌.（精确到0.1小时）

查看试题解析

2023-2024学年高中数学人教A版必修一5.7 三角函数的应用 同步练习

一、选择题

二、多项选择题

三、填空题

四、解答题

2023-2024学年高中数学人教A版必修一5.7 三角函数的应用同步练习