2023-2024学年高中数学人教A版必修一5.5 三角恒等变换 同步练习
试卷更新日期:2023-09-10 类型:同步测试
一、选择题
-
1. 已知 , , 则( )A、 B、 C、 D、2. 已知 , 且 , 则( )A、 B、 C、 D、3. 已知 , 且 , 则( )A、 B、 C、 D、或4. 已知 , 则( )A、 B、 C、3 D、5. 若 , 则( )A、 B、 C、 D、6. 若 , 则的值可能是( )A、 B、 C、2 D、37. 已知锐角满足 , 则( )A、 B、 C、 D、8. 已知 , , , 则( )A、 B、 C、 D、9. 已知 , 是关于的方程的两根,且 , 则( )A、 B、4 C、-12 D、10. 已知为锐角, , 角的终边上有一点 , 则( )A、2 B、 C、 D、11. 已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点 , 则( )A、 B、 C、 D、212. 数学里有一种证明方法叫做Proofwithoutwords,也被称为无字证明,是指仅用图象而无需文字解释就能不证自明的数学命题,由于这种证明方法的特殊性,无字证时被认为比严格的数学证明更为优雅与有条理.如下图,点为半圆上一点, , 垂足为 , 记 , 则由可以直接证明的三角函数公式是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、多项选择题
-
13. 下列各式的值为的是( ).A、sin B、sincos C、 D、14. 若满足 , , 则可以是( )A、 B、 C、 D、π15. 下列等式能够成立的为( )A、 B、 C、 D、16. 已知 、 , ,则( )A、 B、 C、 D、17. 已知函数 , 则( )A、为周期函数 B、的图象关于轴对称 C、的值域为 D、在上单调递增18. 如图所示,设单位圆与轴的正半轴相交于点 , 以轴非负半轴为始边作锐角 , , , 它们的终边分别与单位圆相交于点 , , , 则下列说法正确的是( )
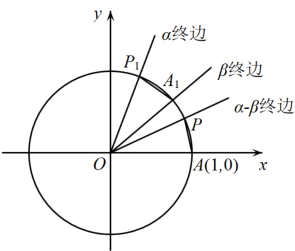 A、的长度为 B、扇形的面积为 C、当与重合时, D、当时,四边形面积的最大值为
A、的长度为 B、扇形的面积为 C、当与重合时, D、当时,四边形面积的最大值为三、填空题
-
19. 若 , 则.20. 若且 , 则 .21. 已知 , 且 , 则 .22. 已知是第二象限的角,且 , 则.23. 已知 , , 则 .
四、解答题
-
24. 已知函数 ,(1)、若 , 且 , 求的值;(2)、求函数的最大值.25. 已知 .(1)、若为第一象限角,求;(2)、求的值.