2023-2024学年高中数学人教A版必修一5.4 三角函数的图像与性质 同步练习
试卷更新日期:2023-09-10 类型:同步测试
一、选择题
-
1. “ , ”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件2. 已知集合 , , 则( )A、 B、 C、 D、3. 函数的大致图象为A、
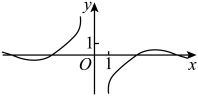 B、
B、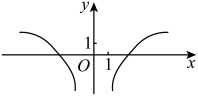 C、
C、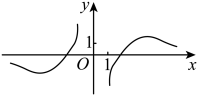 D、
D、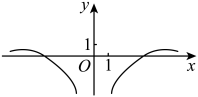 4. 已知 , 则 ( )A、 B、 C、 D、5. 已知函数在区间单调递增,直线和为函数的图像的两条对称轴,则( )A、 B、 C、 D、6. 已知函数为正整数,在区间上单调,且 , 则( )A、 B、 C、 D、7. 已知函数对任意都有 , 则当取到最大值时,图象的一条对称轴为( )A、 B、 C、 D、8. 设.若对任意 , 都存在 , 使得 , 则可以是( )A、 B、 C、 D、
4. 已知 , 则 ( )A、 B、 C、 D、5. 已知函数在区间单调递增,直线和为函数的图像的两条对称轴,则( )A、 B、 C、 D、6. 已知函数为正整数,在区间上单调,且 , 则( )A、 B、 C、 D、7. 已知函数对任意都有 , 则当取到最大值时,图象的一条对称轴为( )A、 B、 C、 D、8. 设.若对任意 , 都存在 , 使得 , 则可以是( )A、 B、 C、 D、二、多项选择题
-
9. 若函数的图象经过点 , 则( )A、函数的最小正周期为 B、点为函数图象的对称中心 C、直线为函数图象的对称轴 D、函数的单调增区间为10. 已知三角函数 , 以下对该函数的说法正确的是( )A、该函数周期为 B、该函数在上单调递增 C、为其一条对称轴 D、将该函数向右平移个单位得到一个奇函数11. 下列各式中正确的是( )A、 B、 C、 D、12. 已知函数 , 其图像上相邻的两个最高点之间的距离为在上是单调函数,则下列说法不正确的是( )A、的最大值为 B、在上的图像与直线没有交点 C、在上没有对称轴 D、在上有一个零点13. 已知是定义在闭区间上的偶函数,且在y轴右侧的图象是函数图象的一部分(如图所示),则( )
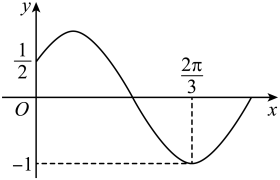 A、的定义域为 B、当时,取得最大值 C、当时,的单调递增区间为 D、当时,有且只有两个零点和14. 已知函数 , 则下列关于函数的图象与性质的叙述中,正确的有( )A、函数的最小正周期为 B、函数在上单调递增 C、函数的图象关于直线对称 D、15. 已知函数的图象经过点 , 则( )A、 B、的最小正周期为 C、的定义域为 D、不等式的解集为 ,16. 函数的最小正周期为 , , 下列说法正确的是( )A、的一个零点为 B、是偶函数 C、在区间上单调递增 D、的一条对称轴为17. 已知函数 , 则下列说法正确的是( )A、函数的一个周期为 B、直线是的一条对称轴 C、点是的一个对称中心 D、在区间上单调递减18. 已知 , 则下列不等式正确的是( )A、 B、 C、 D、
A、的定义域为 B、当时,取得最大值 C、当时,的单调递增区间为 D、当时,有且只有两个零点和14. 已知函数 , 则下列关于函数的图象与性质的叙述中,正确的有( )A、函数的最小正周期为 B、函数在上单调递增 C、函数的图象关于直线对称 D、15. 已知函数的图象经过点 , 则( )A、 B、的最小正周期为 C、的定义域为 D、不等式的解集为 ,16. 函数的最小正周期为 , , 下列说法正确的是( )A、的一个零点为 B、是偶函数 C、在区间上单调递增 D、的一条对称轴为17. 已知函数 , 则下列说法正确的是( )A、函数的一个周期为 B、直线是的一条对称轴 C、点是的一个对称中心 D、在区间上单调递减18. 已知 , 则下列不等式正确的是( )A、 B、 C、 D、三、填空题
-
19. 函数的最小正周期是.20. 函数的最小正周期为 .21. 已知函数的图像关于点对称,且在区间上单调,则 .22. 在平面直角坐标系中,角的顶点与坐标原点重合,始边与轴的正半轴重合,若其终边过点 , 则函数 , 的值域为 .23. 设函数 , 则.24. 已知函数的图象关于点对称,且在区间单调,则的一个取值是.
四、解答题
-
25. 已知函数.(1)、求函数的最小正周期;(2)、若 , 求实数的取值范围.26. 已知函数 , .(1)、求的最大值和对应的取值;(2)、求在的单调递增区间.27. 已知函数 , .(1)、求函数的最小正周期和单调递减区间;(2)、求函数在区间上的最小值和最大值,并求出取得最值时x的值.