浙江省温州市文成县2023-2024学年九年级上学期数学入学监测试卷

试卷更新日期：2023-09-09 类型：开学考试

进入出卷网下载

一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选，均不给分)

1. 计算 $(+ 5) + (- 3)$ 的结果是（）

A、2 B、-2 C、8 D、-8

查看试题解析
2. 如图，已知直线 $c$ 与直线a，b都相交.若 $a / / b ， ∠ 1 = 7 5^{°}$ ，则 $∠ 2$ 的度数为（）

A、 $7 5^{°}$ B、 $10 5^{°}$ C、 $11 5^{°}$ D、 $12 5^{°}$

查看试题解析
3. 2023年8月3日晚天空上演了“土星合月”的天文趣象，土星的直径约为 $116000 k m$ ，大约是月球直径的33倍.数据116000用科学记数法表示为（）

A、 $11.6 \times 1 0^{4}$ B、 $1.16 \times 1 0^{3}$ C、 $1.16 \times 1 0^{4}$ D、 $1.16 \times 1 0^{5}$

查看试题解析
4. 某市一旅行社老板想了解哪些景区最受欢迎，则下列关于旅游景区人数的统计量中最有参考意义的是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
5. 化简 $m^{2} \cdot (- m)^{3}$ 的结果是（）

A、 $m^{5}$ B、 $- m^{5}$ C、 $m^{6}$ D、 $- m^{6}$

查看试题解析
6. 在平面直角坐标系中，点 $P (a ， 3)$ 与点 $Q (- 2 ， b)$ 关于 $x$ 轴对称，则 $a - b$ 的值为（）

A、1 B、-1 C、5 D、-5

查看试题解析
7. 在 $□ A B C D$ 中，若 $∠ A + 3 ∠ B = 32 0^{°}$ ，则 $∠ C$ 的度数为（）

A、 $7 0^{°}$ B、 $8 0^{°}$ C、 $10 0^{°}$ D、 $11 0^{°}$

查看试题解析
8. 图1是第七届国际数学教育大会(ICME)的会徽，图2由主体图案中相邻两个直角三角形组合而成.当 $A B = B C ， ∠ A O B = 3 0^{°} ， O C = 5$ 时，OA的长为（）

A、 $2 \sqrt{3}$ B、 $\sqrt{15}$ C、4 D、 $3 \sqrt{2}$

查看试题解析
9. 如图是小慧用列表法研究关于x，y的二元一次方程 $a x + y = b$ 整数解的规律，如图是小慧列表的部分内容.由表可知m，n的值分别为（）

x

-1

0

1

2

5

y

-7

-3

1

m

n

A、3，9 B、3，17 C、5，9 D、5，17

查看试题解析
10. 将2张相同的正方形纸片和2张相同的小长方形纸片按如图所示摆放在矩形ABCD内，中间留有一个小正方形未被覆盖.经过EF的直线交AD于点 $M$ ，交BC于点 $N$ ，若 $\frac{D M}{D G} = \frac{1}{2}$ ，则 $\frac{A B}{B C}$ 的值为（）

A、 $\frac{5}{7}$ B、 $\frac{3}{4}$ C、 $\frac{2}{3}$ D、 $\frac{7}{9}$

查看试题解析

二、填空题(本题有8小题,每小题5分,共40分)

11. 因式分解： $4 a^{2} - 2 a =$ .

查看试题解析
12. 不等式组 ${\begin{array}{l} x + 3 > 1 \\ \frac{2 x - 1}{3} < 5 \end{array}$ 的解是.

查看试题解析
13. 某学校学生“大运会知识”竞赛成绩的频数直方图(每一组含前一个边界值，不含后一个边界值)如图所示，期中成绩在80分及以上的学生有人.

查看试题解析
14. 计算： $\frac{n^{2}}{2 m^{3}} \cdot \frac{6 m^{2}}{n} =$ .

查看试题解析
15. 若一元二次方程 $x^{2} - 6 x + c = 0$ 有两个相等的实数根，则 $c$ 的值为.

查看试题解析
16. 某一次函数的图象经过点 $(0 ， - 1)$ ，且不经过第一象限，请写一个符合上述条件的函数解析式：.

查看试题解析
17. 如图，在 $△ A B C$ 中， $C A = C B = 5 ， A B = 8$ ，把 $△ A B C$ 绕点 $A$ 逆时针旋转 $6 0^{°}$ 得到 $△ A D E$ ，连结CD，则CD的长为.

查看试题解析
18. 如图，点B在反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象上，点 $A$ 在 $x$ 轴上，过点 $A$ 作 $A C / / O B$ 交 $y$ 轴负半轴于点 $C$ ，若 $O C = O B = A B ， A C = 4$ ，则 $k$ 的值为.

查看试题解析

三、解答题(本题有6小题,共70分.解答时需要写出必要的文字说明、演算步骤或证明过程)

19.

(1)、计算： $\sqrt{12} + | - \sqrt{3} | + 3^{- 1}$ .

(2)、化简： $(m + 2)^{2} - m (m + 3)$ .

查看试题解析
20. 如图， $A B = A C$ ， $C D ⊥ A B$ ， $B E ⊥ A C$ ，垂足分别为 $D$ ， $E$ ．

(1)、求证： $△ A B E ≌ △ A C D$ ；

(2)、若 $A E = 6$ ， $C D = 8$ ，求 $B D$ 的长．

查看试题解析
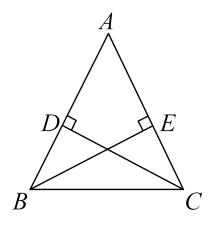21. 某区教育局为了了解某年级学生对科学知识的掌握情况，在全区范围内随机抽取若干名学生进行科学知识测试，按照测试成绩分优秀，良好、合格与不合格四个等级，并绘制了如图所示两幅不完整统计图．

(1)、参与本次测试的学生人数为， m＝．

(2)、请补全条形统计图；

(3)、若全区该年级共有5000名学生，请估计该年级对科学知识掌握情况较好（测试成绩能达到良好及以上等级）的学生人数.

查看试题解析
22. 如图，在5×5的方格纸ABCD中，已知格点P，请按要求画格点三角形（顶点均在小方格的顶点上）．

(1)、在图1中画一个Rt△PQR，使点Q在AD上，点R在BC上．

(2)、在图2中画一个等腰三角形PEF，使点E在AD上，点F在CD上．
注：图1，图2在答题纸上．

查看试题解析

23. 根据背景素材，探索解决问题．

自制杆秤
背景素材	有言道：“杆秤一头称起人间生计，一头称起天地良心”．某兴趣小组将利用物理学中杠杆原理制作简易杆秤．如图，称重物时，移动秤砣可使杆秤平衡，根据杠杆原理推导得： $(m_{0} + m) \times l = M \times (a + y)$ ．其中秤盘质量m₀克，重物质量m克，秤砣质量M克，秤纽与秤盘的水平距离为1厘米，秤纽与零刻线的水平距离为a厘米，秤砣与零刻线的水平距离为y厘米.
	设计简易杆秤要求：设定m₀=10，M=50，最大可称重物质量为1000克，零刻线与末刻线的距离定为50厘米．
问题解决
任务一	确定 $l$ 和 $a$ 的值	⑴当秤盘不放重物，秤砣在零刻线时，杆秤平衡，请列出关于 $l$ ， $a$ 的方程． ⑵当秤盘放入质量为1000克的重物，秤砣从零刻线移至末刻线时，杆秤平衡，请列出关于 $l$ ， $a$ 的方程． ⑶根据（1）和（2）所列方程，求出 $l$ 和 $a$ 的值．
任务二	确定刻线的位置	⑷根据任务一，求y关于m的函数解析式． ⑸从零刻线开始，每隔100克在秤杆上找到对应刻线，请写出相邻刻线间的距离．

查看试题解析

24. 如图，在平面直角坐标系中，已知点A坐标为(6，0)，点C坐标为(2，4)，以OA，OC为邻边作 $□ A B C D$ ，点P在对角线OB上，过点P作x轴的平行线分别交OC，AB于点D，E，过点P作 $P F ⊥ x$ 轴于点F，设PF＝a．

(1)、求直线OC和直线OB的解析式．

(2)、当线段PD，PE，PF构成的三角形是等腰三角形时，求DP的值．

(3)、取PE的中点Q，当∠OQA＝90°时，求a的值.

查看试题解析