广东省广州市2023年中考数学试卷
试卷更新日期:2023-09-09 类型:中考真卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. ( )A、 B、 C、 D、2. 一个几何体的三视图如图所示,则它表示的几何体可能是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 学校举行“书香校园”读书活动,某小组的五位同学在这次活动中读书的本数分别为10,11,9,10,12.下列关于这组数据描述正确的是( )A、众数为10 B、平均数为10 C、方差为2 D、中位数为94. 下列运算正确的是( )A、 B、 C、 D、5. 不等式组的解集在数轴上表示为( )A、
3. 学校举行“书香校园”读书活动,某小组的五位同学在这次活动中读书的本数分别为10,11,9,10,12.下列关于这组数据描述正确的是( )A、众数为10 B、平均数为10 C、方差为2 D、中位数为94. 下列运算正确的是( )A、 B、 C、 D、5. 不等式组的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 6. 已知正比例函数的图象经过点 , 反比例函数的图象位于第一、第三象限,则一次函数的图象一定不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,海中有一小岛 , 在点测得小岛在北偏东方向上,渔船从点出发由西向东航行到达点,在点测得小岛恰好在正北方向上,此时渔船与小岛的距离为 . ( )
6. 已知正比例函数的图象经过点 , 反比例函数的图象位于第一、第三象限,则一次函数的图象一定不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,海中有一小岛 , 在点测得小岛在北偏东方向上,渔船从点出发由西向东航行到达点,在点测得小岛恰好在正北方向上,此时渔船与小岛的距离为 . ( )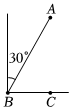 A、 B、 C、 D、8. 随着城际交通的快速发展,某次动车平均提速 , 动车提速后行驶与提速前行驶所用的时间相同设动车提速后的平均速度为 , 则下列方程正确的是( )A、 B、 C、 D、9. 如图,的内切圆与 , , 分别相切于点 , , , 若的半径为 , , 则的值和的大小分别为( )
A、 B、 C、 D、8. 随着城际交通的快速发展,某次动车平均提速 , 动车提速后行驶与提速前行驶所用的时间相同设动车提速后的平均速度为 , 则下列方程正确的是( )A、 B、 C、 D、9. 如图,的内切圆与 , , 分别相切于点 , , , 若的半径为 , , 则的值和的大小分别为( )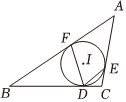 A、 , B、 , C、 , D、 ,10. 已知关于的方程有两个实数根,则的化简结果是( )A、 B、 C、 D、
A、 , B、 , C、 , D、 ,10. 已知关于的方程有两个实数根,则的化简结果是( )A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
11. 近年来,城市电动自行车安全充电需求不断攀升截至2023年5月底,某市已建成安全充电端口逾个,将用科学记数法表示为 .12. 已知点 , 在抛物线上,且 , 则.(填“<”或“>”或“=”).13. 2023年5月30日是第7个全国科技工作者日,某中学举行了科普知识手抄报评比活动,共有100件作品获得一、二、三等奖和优胜奖,根据获奖结果绘制如图所示的条形图,则a的值为若将获奖作品按四个等级所占比例绘制成扇形统计图,则“一等奖”对应扇形的圆心角度数为
 14. 如图,正方形的边长为 , 点在边上,且 , 为对角线上一动点,连接 , , 则的最小值为 .
14. 如图,正方形的边长为 , 点在边上,且 , 为对角线上一动点,连接 , , 则的最小值为 . 15. 如图,已知是的角平分线, , 分别是和的高, , , 则点到直线的距离为 .
15. 如图,已知是的角平分线, , 分别是和的高, , , 则点到直线的距离为 . 16. 如图,在中, , , , 点是边上一动点,点 , 分别是 , 的中点,当时,的长是若点在边上,且 , 点 , 分别是 , 的中点,当时,四边形面积的取值范围是 .
16. 如图,在中, , , , 点是边上一动点,点 , 分别是 , 的中点,当时,的长是若点在边上,且 , 点 , 分别是 , 的中点,当时,四边形面积的取值范围是 .
三、计算题(本大题共1小题,共4.0分)
-
17. 解方程:
四、解答题(本大题共8小题,共68.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 如图,是的中点, , 求证: .
 19. 如图,在平面直角坐标系中,点 , , 所在圆的圆心为将向右平移5个单位,得到(点A平移后的对应点为C).
19. 如图,在平面直角坐标系中,点 , , 所在圆的圆心为将向右平移5个单位,得到(点A平移后的对应点为C). (1)、点的坐标是 , 所在圆的圆心坐标是;(2)、在图中画出 , 并连接 , ;(3)、求由 , , , 首尾依次相接所围成的封闭图形的周长.(结果保留π)20. 已知 , 代数式: , , .(1)、因式分解;(2)、在 , , 中任选两个代数式,分别作为分子、分母,组成一个分式,并化简该分式.21. 甲、乙两位同学相约打乒乓球.(1)、有款式完全相同的4个乒乓球拍分别记为 , , , , 若甲先从中随机选取1个,乙再从余下的球拍中随机选取1个,求乙选中球拍C的概率;(2)、双方约定:两人各投掷一枚质地均匀的硬币,如果两枚硬币全部正面向上或全部反面向上,那么甲先发球,否则乙先发球这个约定是否公平?为什么?22. 因活动需要购买某种水果,数学活动小组的同学通过市场调查得知:在甲商店购买该水果的费用元与该水果的质量千克之间的关系如图所示;在乙商店购买该水果的费用元与该水果的质量千克之间的函数解析式为 .
(1)、点的坐标是 , 所在圆的圆心坐标是;(2)、在图中画出 , 并连接 , ;(3)、求由 , , , 首尾依次相接所围成的封闭图形的周长.(结果保留π)20. 已知 , 代数式: , , .(1)、因式分解;(2)、在 , , 中任选两个代数式,分别作为分子、分母,组成一个分式,并化简该分式.21. 甲、乙两位同学相约打乒乓球.(1)、有款式完全相同的4个乒乓球拍分别记为 , , , , 若甲先从中随机选取1个,乙再从余下的球拍中随机选取1个,求乙选中球拍C的概率;(2)、双方约定:两人各投掷一枚质地均匀的硬币,如果两枚硬币全部正面向上或全部反面向上,那么甲先发球,否则乙先发球这个约定是否公平?为什么?22. 因活动需要购买某种水果,数学活动小组的同学通过市场调查得知:在甲商店购买该水果的费用元与该水果的质量千克之间的关系如图所示;在乙商店购买该水果的费用元与该水果的质量千克之间的函数解析式为 . (1)、求与之间的函数解析式;(2)、现计划用元购买该水果,选甲、乙哪家商店能购买该水果更多一些?23. 如图,是菱形的对角线.(1)、尺规作图:将绕点逆时针旋转得到 , 点旋转后的对应点为保留作图痕迹,不写作法;(2)、在(1)所作的图中,连接 , .
(1)、求与之间的函数解析式;(2)、现计划用元购买该水果,选甲、乙哪家商店能购买该水果更多一些?23. 如图,是菱形的对角线.(1)、尺规作图:将绕点逆时针旋转得到 , 点旋转后的对应点为保留作图痕迹,不写作法;(2)、在(1)所作的图中,连接 , .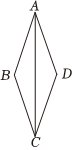
求证:∽;
若 , 求的值.
24. 已知点在函数的图象上.(1)、若m=-2,求n的值;(2)、抛物线与x轴交于两点M,N(M在N的左边),与y轴交于点G,记抛物线的顶点为E.
①m为何值时,点E到达最高处;②设的外接圆圆心为C,⊙C与轴的另一个交点为F,当时,是否存在四边形为平行四边形?若存在,求此时顶点E的坐标;若不存在,请说明理由.
25. 如图,在正方形中,是边上一动点不与点 , 重合边关于对称的线段为 , 连接 . (1)、若 , 求证:是等边三角形;(2)、延长 , 交射线于点 .
(1)、若 , 求证:是等边三角形;(2)、延长 , 交射线于点 .①△BGF能否为等腰三角形?如果能,求此时的度数;如果不能,请说明理由;
若 , 求面积的最大值,并求此时的长.
-