2023-2024学年高中数学人教A版必修一5.1 任意角和弧度制同步练习

试卷更新日期：2023-09-08 类型：同步测试

进入出卷网下载

一、选择题

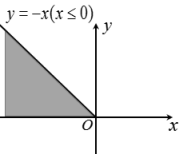
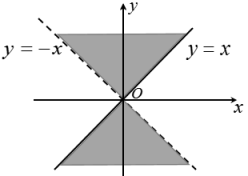
1. 在平面直角坐标系中，角 $α$ 和 $β$ 的顶点与原点重合，始边与 $x$ 轴的正半轴重合，若角 $α$ 和 $β$ 的终边关于 $y$ 轴对称，则下列关系式一定正确的是（）

A、 $α - β = 2 k π + \frac{π}{2}$ （ $k ∈ Z$ ） B、 $α + β = 2 k π + \frac{π}{2}$ （ $k ∈ Z$ ） C、 $α - β = 2 k π + π$ （ $k ∈ Z$ ） D、 $α + β = 2 k π + π$ （ $k ∈ Z$ ）

查看试题解析
2. 军事上角的度量常用密位制，密位制的单位是“密位”1密位就是圆周的 $\frac{1}{6000}$ 所对的圆心角的大小，.若角 $α = 1000$ 密位，则 $α =$ （）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{5 π}{12}$

查看试题解析
3. 若 $α$ 是第四象限角，则 $π - α$ 是（）

A、第一象限角 B、第二象限角 C、第三象限角 D、第四象限角

查看试题解析
4. 已知角 $α =$ 2022°，则角 $α$ 的终边落在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 圆锥侧面展开图扇形的圆心角为60°，底面圆的半径为8，则圆锥的侧面积为（）

A、 $384 π$ B、 $392 π$ C、 $398 π$ D、 $404 π$

查看试题解析
6. 《几何原本》是古希腊数学家欧几里得的一部不朽之作，书中称轴截面为等腰直角三角形的圆锥为直角圆锥，则直角圆锥侧面展开图的圆心角的弧度数为（）

A、 $\frac{π}{2}$ B、 $\frac{\sqrt{2}}{2} π$ C、 $\sqrt{2} π$ D、 $2 \sqrt{2} π$

查看试题解析
7. 下列命题中正确的是（）

A、终边重合的两个角相等 B、锐角是第一象限的角 C、第二象限的角是钝角 D、小于90°的角都是锐角

查看试题解析
8. 如图，在扇形 $A O B$ 中，C是弦 $A B$ 的中点，D在 $\overset{⌢}{A B}$ 上， $C D ⊥ A B$ ．其中 $O A = O B = r$ ， $\overset{⌢}{A B}$ 长为 $l$ $(l < r)$ ．则 $C D$ 的长度约为（提示： $x \in (0 ， \frac{1}{2})$ 时， $c o s x \approx 1 - \frac{x^{2}}{2}$ ）（）

A、 $r - \frac{l^{2}}{8 r}$ B、 $\frac{l^{2}}{8 r}$ C、 $r - \frac{l^{2}}{4 r}$ D、 $\frac{l^{2}}{4 r}$

查看试题解析
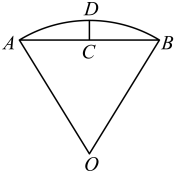9. 相传早在公元前3世纪，古希腊天文学家厄拉多塞内斯就首次测出了地球半径.厄拉多塞内斯选择在夏至这一天利用同一子午线（经线）的两个城市（赛伊城和亚历山大城）进行观测，当太阳光直射塞伊城某水井 $S$ 时，亚历山大城某处 $A$ 的太阳光线与地面成角 $θ = 82 . 8^{∘}$ ，又知某商队旅行时测得 $A$ 与 $S$ 的距离即劣弧 $\overset{⌢}{A S}$ 的长为5000古希腊里，若圆周率取3.125，则可估计地球半径约为（）

A、35000古希腊里 B、40000古希腊里 C、45000古希腊里 D、50000古希腊里

查看试题解析
10. 在轴截面顶角为直角的圆锥内，作一内接圆柱，若圆柱的表面积等于圆锥的侧面积，则圆柱的底面半径与圆锥的底面半径的比值为（）

A、 $\frac{1}{4}$ B、 $\frac{\sqrt{2}}{4}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析

二、多项选择题

11. 下列命题正确的是（）

A、第一象限的角都是锐角 B、小于 $\frac{π}{2}$ 的角是锐角 C、 $2023 °$ 是第三象限的角 D、钝角是第二象限角

查看试题解析
12. 与 $- 835 °$ 终边相同的角有（）

A、 $- 245 °$ B、 $245 °$ C、 $- 115 °$ D、 $- 475 °$

查看试题解析
13. 下列说法中正确的是（）

A、半径为2，圆心角为1弧度的扇形面积为1 B、若 $α$ 是第二象限角，则 $\frac{α}{2}$ 是第一象限角 C、 $\forall x \in R$ ， $x^{2} - 4 x + 5 \geq 0$ D、命题： $\forall x > 0$ ， $l n x \leq x - 1$ 的否定是： $\exists x_{0} > 0$ ， $l n x_{0} > x_{0} - 1$

查看试题解析
14. 小夏同学在学习了《任意角和弧度制》后，对家里的扇形瓷器盘（图1）产生了浓厚的兴趣，并临摹出该瓷器盘的大致形状，如图2所示，在扇形 $O A B$ 中， $∠ A O B = \frac{π}{3}$ ， $O B = O A = 2$ ，则（）

A、 $∠ A O B = 30 °$ B、弧长 $\overset{⌢}{A B} = \frac{2 π}{3}$ C、扇形 $O A B$ 的周长为 $\frac{2 π}{3} + 4$ D、扇形 $O A B$ 的面积为 $\frac{4 π}{3}$

查看试题解析

三、填空题

15. 已知一扇形的圆心角为2，半径为r，弧长为l，则 $l + \frac{2}{r}$ 的最小值为．

查看试题解析
16. 角 $2023 °$ 是第象限角.

查看试题解析
17. 已知扇形的面积为 $10 c m^{2}$ ，该扇形圆心角的弧度数是2，则扇形的弧长为cm．

查看试题解析
18. 若 $α = 2022 °$ ，则与 $α$ 有相同终边的最小正角 $β =$ ．

查看试题解析
19. 在 $0 ° ~ 180 °$ 范围内，与 $- 930 °$ 终边相同的角是．

查看试题解析
20. 已知 $△ A B C$ 是边长为2的等边三角形.如图，将 $△ A B C$ 的顶点 $A$ 与原点重合， $A B$ 在 $x$ 轴上，然后将三角形沿着 $x$ 轴正方向滚动，每当顶点 $A$ 再次回落到 $x$ 轴上时，将相邻两个点 $A$ 之间的距离称为“一个周期”，则完成“一个周期”时，顶点 $A$ 的路径长度为.

查看试题解析
21. 中国传统扇文化有着极其深厚的底蕴. 一般情况下，折扇可看作是从一个圆面中剪下的扇形制作而成，设扇形的面积为 $S_{1}$ ，圆面中剩余部分的面积为 $S_{2}$ ，当 $S_{1}$ 与 $S_{2}$ 的比值为 $\frac{\sqrt{5} - 1}{2}$ 时，扇面看上去形状较为美观，那么此时扇形的圆心角的弧度数为

查看试题解析

四、解答题

22. 已知 $α = \frac{π}{3}$ .

(1)、写出与角 $α$ 终边相同的角的集合；

(2)、写出在 $(- 4 π ， 2 π)$ 内与角 $α$ 终边相同的角.

查看试题解析
23. 如图，写出终边落在阴影部分的角的集合

(1)、

(2)、

查看试题解析
24. 若 $α = k \cdot 360^{\circ} + 24^{\circ}$ ， $k \in Z$ ，试确定 $2 α$ ， $\frac{α}{2}$ 分别是第几象限角．

查看试题解析
25. 已知角 $α$ 的集合为 $M = {α | α = 30 ° + k \cdot 90 ° ， k \in Z}$ ，回答下列问题：

(1)、集合M中有几类终边不相同的角？

(2)、集合M中大于－360°且小于360°的角是哪几个？

(3)、求集合M中的第二象限角 $β$ ．

查看试题解析

2023-2024学年高中数学人教A版必修一5.1 任意角和弧度制 同步练习

一、选择题

二、多项选择题

三、填空题

四、解答题

2023-2024学年高中数学人教A版必修一5.1 任意角和弧度制同步练习