湖北省恩施州2023年中考数学试卷
试卷更新日期:2023-09-08 类型:中考真卷
一、单选题
-
1. 如图,数轴上点A所表示的数的相反数是( )
 A、9 B、 C、 D、2. 下列4个图形中,是中心对称图形的是( )A、
A、9 B、 C、 D、2. 下列4个图形中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列实数: , 0, , , 其中最小的是( )A、 B、0 C、 D、4. 用5个完全相同的小正方体组成如图所示的立体图形,它的左视图是( )
3. 下列实数: , 0, , , 其中最小的是( )A、 B、0 C、 D、4. 用5个完全相同的小正方体组成如图所示的立体图形,它的左视图是( )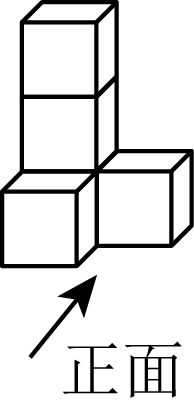 A、
A、 B、
B、 C、
C、 D、
D、 5. 下列运算正确的是( )A、 B、 C、 D、6. 县林业部门考察银杏树苗在一定条件下移植的成活率,所统计的银杏树苗移植成活的相关数据如下表所示:
5. 下列运算正确的是( )A、 B、 C、 D、6. 县林业部门考察银杏树苗在一定条件下移植的成活率,所统计的银杏树苗移植成活的相关数据如下表所示:移植的棵数a
100
300
600
1000
7000
15000
成活的棵数b
84
279
505
847
6337
13581
成活的频率
0.84
0.93
0.842
0.847
0.905
0.905
根据表中的信息,估计银杏树苗在一定条件下移植成活的概率为(精确到0.1)( )
A、0.905 B、0.90 C、0.9 D、0.87. 将含角的直角三角板按如图方式摆放,已知 , , 则( )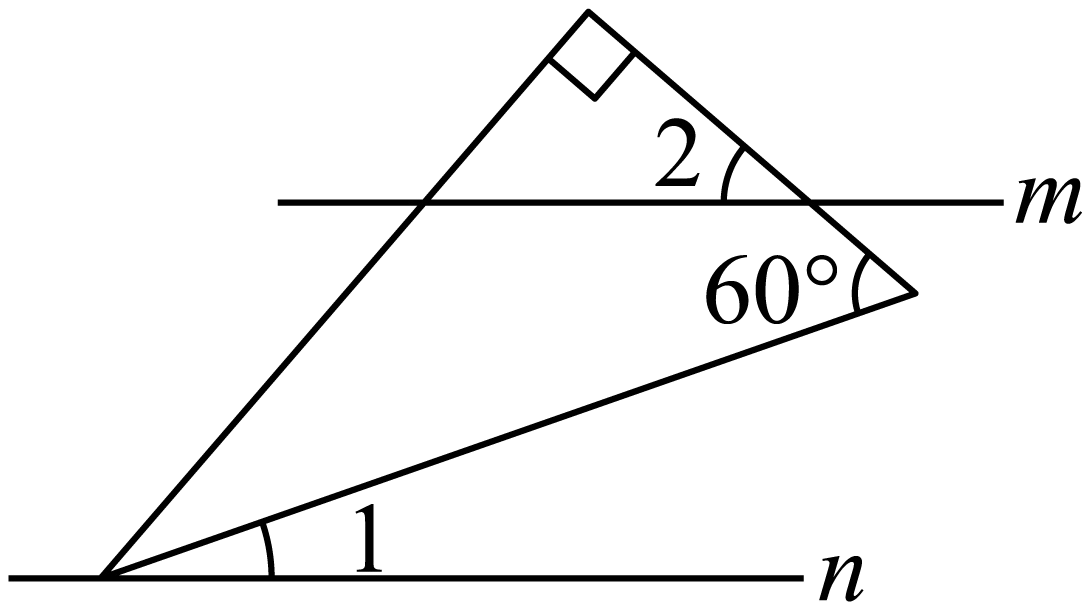 A、 B、 C、 D、8. 分式方程的解是( )A、 B、 C、 D、9. 如图,取一根长的匀质木杆,用细绳绑在木杆的中点O并将其吊起来,在中点O的左侧距离中点处挂一个重的物体,在中点O的右侧用一个弹簧秤向下拉,使木杆处于水平状态.弹簧秤与中点O的距离L(单位:)及弹簧秤的示数F(单位:N)满足 . 以L的数值为横坐标,F的数值为纵坐标建立直角坐标系.则F关于L的函数图象大致是( )
A、 B、 C、 D、8. 分式方程的解是( )A、 B、 C、 D、9. 如图,取一根长的匀质木杆,用细绳绑在木杆的中点O并将其吊起来,在中点O的左侧距离中点处挂一个重的物体,在中点O的右侧用一个弹簧秤向下拉,使木杆处于水平状态.弹簧秤与中点O的距离L(单位:)及弹簧秤的示数F(单位:N)满足 . 以L的数值为横坐标,F的数值为纵坐标建立直角坐标系.则F关于L的函数图象大致是( ) A、
A、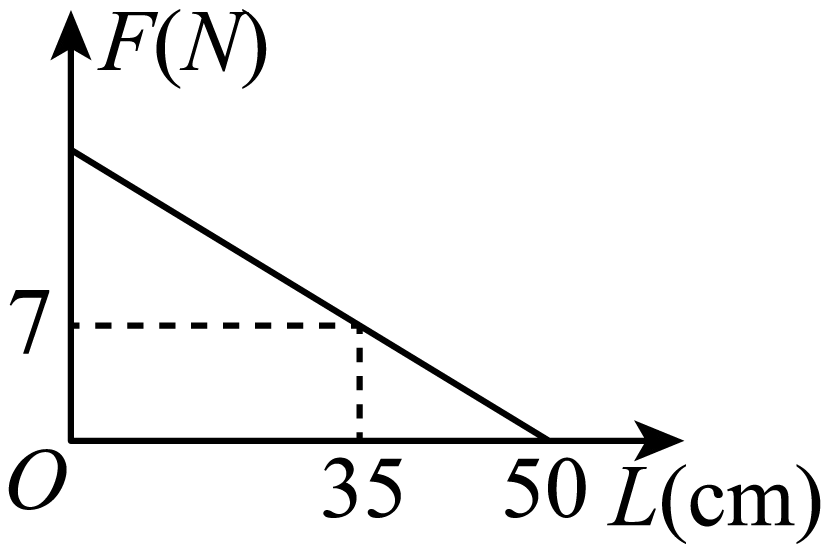 B、
B、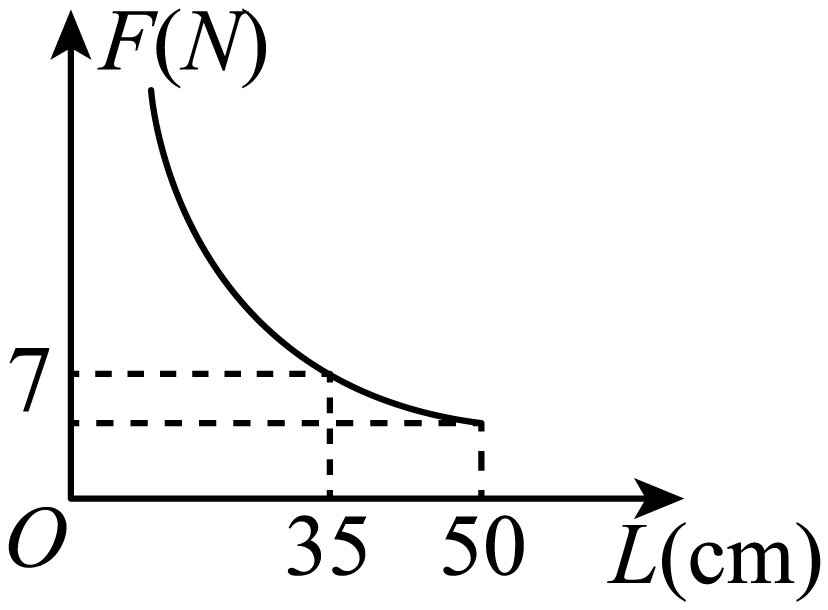 C、
C、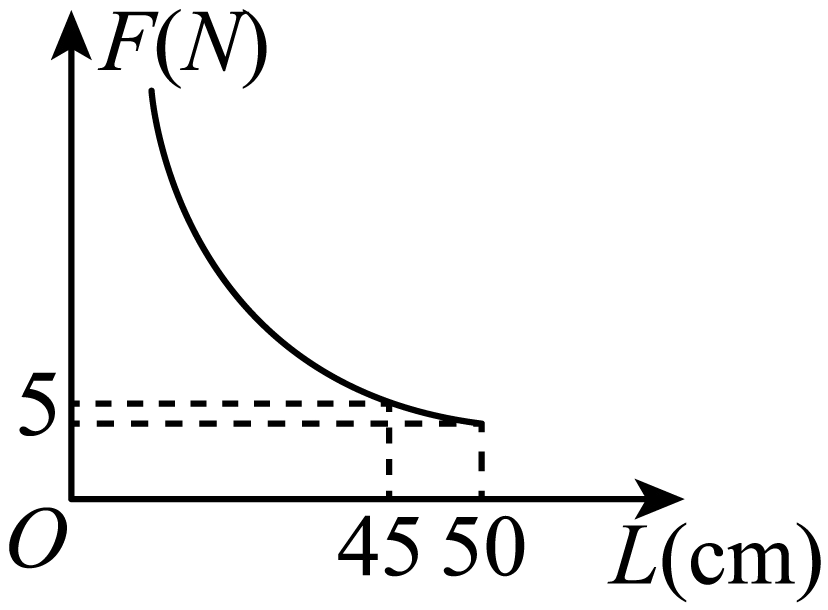 D、
D、 10. 如图,在中,分别交于点D , E , 交于点F , , , 则的长为( )
10. 如图,在中,分别交于点D , E , 交于点F , , , 则的长为( )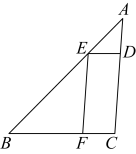 A、 B、 C、2 D、311. 如图,等圆和相交于A , B两点,经过的圆心 , 若 , 则图中阴影部分的面积为( )
A、 B、 C、2 D、311. 如图,等圆和相交于A , B两点,经过的圆心 , 若 , 则图中阴影部分的面积为( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中,O为坐标原点,抛物线的对称轴为 , 与x轴的一个交点位于 , 两点之间.下列结论:①; ②;③; ④若 , 为方程的两个根,则 . 其中正确的有( )个.
A、 B、 C、 D、12. 如图,在平面直角坐标系中,O为坐标原点,抛物线的对称轴为 , 与x轴的一个交点位于 , 两点之间.下列结论:①; ②;③; ④若 , 为方程的两个根,则 . 其中正确的有( )个. A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 计算: × = .14. 因式分解: .15. 《九章算术》被称为人类科学史上应用数学的“算经之首”.书中记载:“今有户不知高、广,竿不知长短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?”译文:今有门,不知其高宽;有竿,不知其长短,横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.问门高、宽和对角线的长各是多少(如图)?答:门高、宽和对角线的长分别是尺.
 16. 观察下列两行数,探究第②行数与第①行数的关系:
16. 观察下列两行数,探究第②行数与第①行数的关系:, 4, , 16, , 64,……①
0,7, , 21, , 71,……②
根据你的发现,完成填空:第①行数的第10个数为;取每行数的第2023个数,则这两个数的和为 .
三、解答题
-
17. 先化简,再求值: , 其中 .18. 如图,在矩形中,点是的中点,将矩形沿所在的直线折叠,的对应点分别为 , , 连接交于点 .
 (1)、若 , 求的度数;(2)、连接EF , 试判断四边形的形状,并说明理由.19. 春节、清明、端午、中秋是我国四大传统节日,每个传统节日都有丰富的文化内涵,体现了厚重的家国情怀;在文化的传承与创新中让我们更加热爱传统文化,更加坚定文化自信.因此,端午节前,学校举行“传经典·乐端午”系列活动,活动设计的项目及要求如下:A-包粽子,B-划旱船,C-诵诗词,D-创美文;人人参加,每人限选一项.为了解学生的参与情况,校团支部随机抽取了部分学生进行调查,并根据调查结果绘制了如下不完整的统计图,如图.请根据统计图中的信息,回答下列问题:
(1)、若 , 求的度数;(2)、连接EF , 试判断四边形的形状,并说明理由.19. 春节、清明、端午、中秋是我国四大传统节日,每个传统节日都有丰富的文化内涵,体现了厚重的家国情怀;在文化的传承与创新中让我们更加热爱传统文化,更加坚定文化自信.因此,端午节前,学校举行“传经典·乐端午”系列活动,活动设计的项目及要求如下:A-包粽子,B-划旱船,C-诵诗词,D-创美文;人人参加,每人限选一项.为了解学生的参与情况,校团支部随机抽取了部分学生进行调查,并根据调查结果绘制了如下不完整的统计图,如图.请根据统计图中的信息,回答下列问题: (1)、请直接写出统计图中m的值,并补全条形统计图;(2)、若学校有1800名学生,请估计选择D类活动的人数;(3)、甲、乙、丙、丁四名学生都是包粽子的能手,现从他们4人中选2人参加才艺展示,请用列表或画树状图的方法,求甲、乙2人同时被选中的概率.20. 小王同学学习了锐角三角函数后,通过观察广场的台阶与信号塔之间的相对位置,他认为利用台阶的可测数据与在点 , 处测出点的仰角度数,可以求出信号塔的高.如图,的长为 , 高为 . 他在点处测得点的仰角为 , 在点处测得点的仰角为 , 在同一平面内.你认为小王同学能求出信号塔的高吗?若能,请求出信号塔的高;若不能,请说明理由.(参考数据: , , , 结果保留整数)
(1)、请直接写出统计图中m的值,并补全条形统计图;(2)、若学校有1800名学生,请估计选择D类活动的人数;(3)、甲、乙、丙、丁四名学生都是包粽子的能手,现从他们4人中选2人参加才艺展示,请用列表或画树状图的方法,求甲、乙2人同时被选中的概率.20. 小王同学学习了锐角三角函数后,通过观察广场的台阶与信号塔之间的相对位置,他认为利用台阶的可测数据与在点 , 处测出点的仰角度数,可以求出信号塔的高.如图,的长为 , 高为 . 他在点处测得点的仰角为 , 在点处测得点的仰角为 , 在同一平面内.你认为小王同学能求出信号塔的高吗?若能,请求出信号塔的高;若不能,请说明理由.(参考数据: , , , 结果保留整数) 21. 如图,在平面直角坐标系中,O为坐标原点,直线交y轴于点A , 交x轴于点B , 与双曲线在一,三象限分别交于C , D两点, , 连接 , .
21. 如图,在平面直角坐标系中,O为坐标原点,直线交y轴于点A , 交x轴于点B , 与双曲线在一,三象限分别交于C , D两点, , 连接 , . (1)、求k的值;(2)、求的面积.22. 为积极响应州政府“悦享成长·书香恩施”的号召,学校组织150名学生参加朗诵比赛,因活动需要,计划给每个学生购买一套服装.经市场调查得知,购买1套男装和1套女装共需220元;购买6套男装与购买5套女装的费用相同.(1)、男装、女装的单价各是多少?(2)、如果参加活动的男生人数不超过女生人数的 , 购买服装的总费用不超过17000元,那么学校有几种购买方案?怎样购买才能使费用最低,最低费用是多少?
(1)、求k的值;(2)、求的面积.22. 为积极响应州政府“悦享成长·书香恩施”的号召,学校组织150名学生参加朗诵比赛,因活动需要,计划给每个学生购买一套服装.经市场调查得知,购买1套男装和1套女装共需220元;购买6套男装与购买5套女装的费用相同.(1)、男装、女装的单价各是多少?(2)、如果参加活动的男生人数不超过女生人数的 , 购买服装的总费用不超过17000元,那么学校有几种购买方案?怎样购买才能使费用最低,最低费用是多少?