江苏省常州市2023年中考数学试卷
试卷更新日期:2023-09-08 类型:中考真卷
一、单选题
-
1. 计算的结果是( )A、 B、 C、 D、2. 若代数式的值是0,则实数x的值是( )A、 B、0 C、1 D、23.
某运动会颁奖台如图所示,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列实数中,其相反数比本身大的是( )A、 B、 C、 D、5. 2022年10月31日,搭载空间站梦天实验舱的长征五号B遥四运载火箭,在我国文昌航天发射场发射成功.长征五号B运载火箭可提供起飞推力.已知起飞推力约等于 , 则长征五号B运载火箭可提供的起飞推力约为( )A、 B、 C、 D、6. 在平面直角坐标系中,若点P的坐标为 , 则点P关于y轴对称的点的坐标为( )A、 B、 C、 D、7. 小明按照以下步骤画线段AB的三等分点:
4. 下列实数中,其相反数比本身大的是( )A、 B、 C、 D、5. 2022年10月31日,搭载空间站梦天实验舱的长征五号B遥四运载火箭,在我国文昌航天发射场发射成功.长征五号B运载火箭可提供起飞推力.已知起飞推力约等于 , 则长征五号B运载火箭可提供的起飞推力约为( )A、 B、 C、 D、6. 在平面直角坐标系中,若点P的坐标为 , 则点P关于y轴对称的点的坐标为( )A、 B、 C、 D、7. 小明按照以下步骤画线段AB的三等分点:画法
图形
1.以A为端点画一条射线;
2.用圆规在射线上依次截取3条等长线段AC、CD、DE , 连接BE;
3.过点C、D分别画BE的平行线,交线段AB于点M、N , M、N就是线段AB的三等分点.
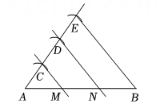
这一画图过程体现的数学依据是( )
A、两直线平行,同位角相等 B、两条平行线之间的距离处处相等 C、垂直于同一条直线的两条直线平行 D、两条直线被一组平行线所截,所得的对应线段成比例8. 折返跑是一种跑步的形式.如图,在一定距离的两个标志物①、②之间,从①开始,沿直线跑至②处,用手碰到②后立即转身沿直线跑至①处,用手碰到①后继续转身跑至②处,循环进行,全程无需绕过标志物.小华练习了一次的折返跑,用时在整个过程中,他的速度大小v()随时间t()变化的图像可能是( ) A、
A、 B、
B、 C、
C、 D、
D、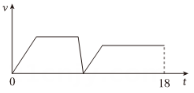
二、填空题
-
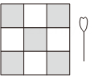
9. 9的算术平方根是 .10. 分解因式:x2y-4y= .11. 计算: .12. 若矩形的面积是10,相邻两边的长分别为x、y,则y与x的函数表达式为 .13. 若圆柱的底面半径和高均为a,则它的体积是(用含a的代数式表示).14. 如图,飞镖游戏板中每一块小正方形的面积相等.任意投掷飞镖1次且击中游戏板,则击中阴影部分的概率是 .
 15. 如图,在中, , 点D在边AB上,连接CD . 若 , , 则 .
15. 如图,在中, , 点D在边AB上,连接CD . 若 , , 则 .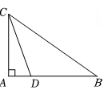 16. 如图,是的直径,是的内接三角形.若 , , 则的直径 .
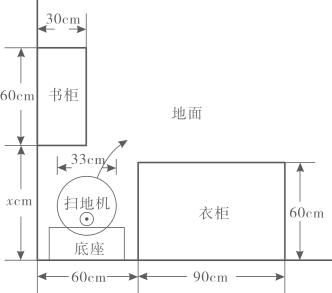
16. 如图,是的直径,是的内接三角形.若 , , 则的直径 .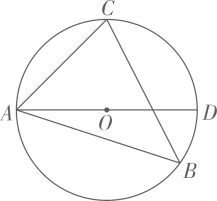 17. 如图,小红家购置了一台圆形自动扫地机,放置在屋子角落(书柜、衣柜与地面均无缝隙).在没有障碍物阻挡的前提下,扫地机能自动从底座脱离后打扫全屋地面.若这台扫地机能从角落自由进出,则图中的x至少为(精确到个位,参考数据:).
17. 如图,小红家购置了一台圆形自动扫地机,放置在屋子角落(书柜、衣柜与地面均无缝隙).在没有障碍物阻挡的前提下,扫地机能自动从底座脱离后打扫全屋地面.若这台扫地机能从角落自由进出,则图中的x至少为(精确到个位,参考数据:).

 18. 如图,在中, , D是AC延长线上的一点, . M是边BC上的一点(点M与点B、C不重合),以CD、CM为邻边作 . 连接并取的中点P , 连接 , 则的取值范围是 .
18. 如图,在中, , D是AC延长线上的一点, . M是边BC上的一点(点M与点B、C不重合),以CD、CM为邻边作 . 连接并取的中点P , 连接 , 则的取值范围是 .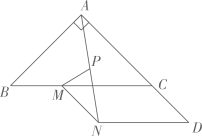
三、解答题
-
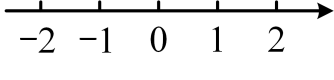
19. 先化简,再求值: , 其中 .20. 解不等式组 , 把解集在数轴上表示出来,并写出整数解.
 21. 为合理安排进、离校时间,学校调查小组对某一天八年级学生上学、放学途中的用时情况进行了调查.本次调查在八年级随机抽取了名学生,建立以上学途中用时为横坐标、放学途中用时为纵坐标的平面直角坐标系,并根据调查结果画出相应的点,如图所示:
21. 为合理安排进、离校时间,学校调查小组对某一天八年级学生上学、放学途中的用时情况进行了调查.本次调查在八年级随机抽取了名学生,建立以上学途中用时为横坐标、放学途中用时为纵坐标的平面直角坐标系,并根据调查结果画出相应的点,如图所示: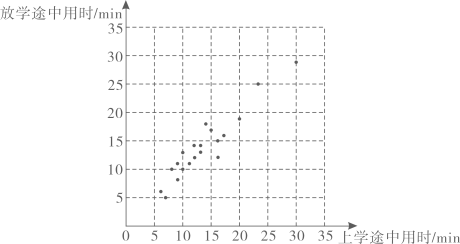 (1)、根据图中信息,下列说法中正确的是(写出所有正确说法的序号):
(1)、根据图中信息,下列说法中正确的是(写出所有正确说法的序号):①这名学生上学途中用时都没有超过;
②这名学生上学途中用时在以内的人数超过一半;
③这名学生放学途中用时最短为;
④这名学生放学途中用时的中位数为 .
(2)、已知该校八年级共有名学生,请估计八年级学生上学途中用时超过的人数(3)、调查小组发现,图中的点大致分布在一条直线附近.请直接写出这条直线对应的函数表达式并说明实际意义.22. 在5张相同的小纸条上,分别写有:①;②;③1;④乘法;⑤加法.将这5张小纸条做成5支签,①、②、③放在不透明的盒子A中搅匀,④、⑤放在不透明的盒子B中搅匀.(1)、从盒子中任意抽出支签,抽到无理数的概率是;(2)、先从盒子中任意抽出支签,再从盒子中任意抽出支签,求抽到的个实数进行相应的运算后结果是无理数的概率.23. 如图,、、、是直线上的四点, .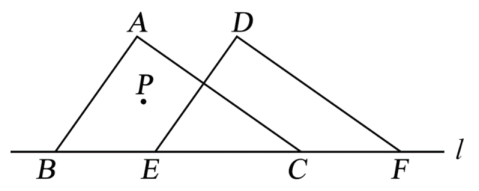 (1)、求证:;(2)、点、分别是、的内心.
(1)、求证:;(2)、点、分别是、的内心.①用直尺和圆规作出点(保留作图痕迹,不要求写作法);
②连接 , 则与的关系是__▲__.
24. 如图,在打印图片之前,为确定打印区域,需设置纸张大小和页边距(纸张的边线到打印区域的距离),上、下,左、右页边距分别为 . 若纸张大小为 , 考虑到整体的美观性,要求各页边距相等并使打印区域的面积占纸张的 , 则需如何设置页边距?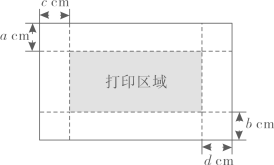 25. 在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点、 . C是y轴上的一点,连接、 .(1)、求一次函数、反比例函数的表达式;(2)、若的面积是6,求点C的坐标.26. 对于平面内的一个四边形,若存在点 , 使得该四边形的一条对角线绕点旋转一定角度后能与另一条对角线重合,则称该四边形为“可旋四边形”,点是该四边形的一个“旋点”.例如,在矩形中,对角线、相交于点 , 则点是矩形的一个“旋点”.
25. 在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点、 . C是y轴上的一点,连接、 .(1)、求一次函数、反比例函数的表达式;(2)、若的面积是6,求点C的坐标.26. 对于平面内的一个四边形,若存在点 , 使得该四边形的一条对角线绕点旋转一定角度后能与另一条对角线重合,则称该四边形为“可旋四边形”,点是该四边形的一个“旋点”.例如,在矩形中,对角线、相交于点 , 则点是矩形的一个“旋点”.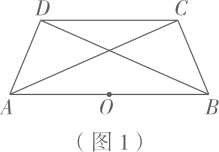
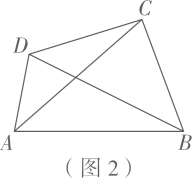 (1)、若菱形为“可旋四边形”,其面积是 , 则菱形的边长是;(2)、如图1,四边形为“可旋四边形”,边的中点是四边形的一个“旋点”.求的度数;(3)、如图2,在四边形中, , 与不平行.四边形是否为“可旋四边形”?请说明理由.27. 如图,二次函数的图象与x轴相交于点 , 其顶点是C .
(1)、若菱形为“可旋四边形”,其面积是 , 则菱形的边长是;(2)、如图1,四边形为“可旋四边形”,边的中点是四边形的一个“旋点”.求的度数;(3)、如图2,在四边形中, , 与不平行.四边形是否为“可旋四边形”?请说明理由.27. 如图,二次函数的图象与x轴相交于点 , 其顶点是C .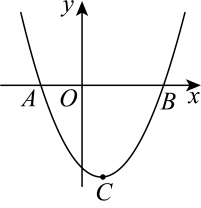
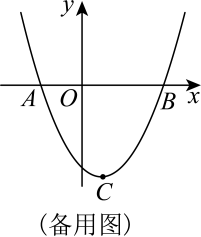 (1)、;(2)、D是第三象限抛物线上的一点,连接OD , ;将原抛物线向左平移,使得平移后的抛物线经过点D , 过点作x轴的垂线l . 已知在l的左侧,平移前后的两条抛物线都下降,求k的取值范围;(3)、将原抛物线平移,平移后的抛物线与原抛物线的对称轴相交于点Q , 且其顶点P落在原抛物线上,连接PC、QC、PQ . 已知是直角三角形,求点P的坐标.28. 如图1,小丽借助几何软件进行数学探究:第一步,画出矩形和矩形 , 点、在边上(),且点、、、在直线的同侧;第二步,设置 , 矩形能在边上左右滑动;第三步,画出边的中点 , 射线与射线相交于点(点、不重合),射线与射线相交于点(点、不重合),观测、的长度.
(1)、;(2)、D是第三象限抛物线上的一点,连接OD , ;将原抛物线向左平移,使得平移后的抛物线经过点D , 过点作x轴的垂线l . 已知在l的左侧,平移前后的两条抛物线都下降,求k的取值范围;(3)、将原抛物线平移,平移后的抛物线与原抛物线的对称轴相交于点Q , 且其顶点P落在原抛物线上,连接PC、QC、PQ . 已知是直角三角形,求点P的坐标.28. 如图1,小丽借助几何软件进行数学探究:第一步,画出矩形和矩形 , 点、在边上(),且点、、、在直线的同侧;第二步,设置 , 矩形能在边上左右滑动;第三步,画出边的中点 , 射线与射线相交于点(点、不重合),射线与射线相交于点(点、不重合),观测、的长度.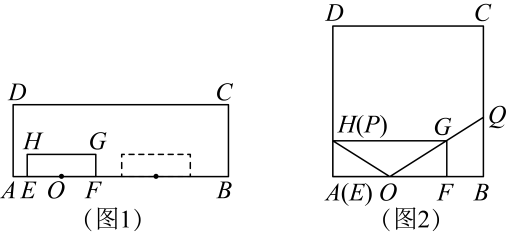 (1)、如图 , 小丽取 , 滑动矩形 , 当点、重合时,;(2)、小丽滑动矩形 , 使得恰为边的中点.她发现对于任意的总成立.请说明理由;(3)、经过数次操作,小丽猜想,设定、的某种数量关系后,滑动矩形 , 总成立.小丽的猜想是否正确?请说明理由.
(1)、如图 , 小丽取 , 滑动矩形 , 当点、重合时,;(2)、小丽滑动矩形 , 使得恰为边的中点.她发现对于任意的总成立.请说明理由;(3)、经过数次操作,小丽猜想,设定、的某种数量关系后,滑动矩形 , 总成立.小丽的猜想是否正确?请说明理由.