江苏省南通市2023年中考数学试卷
试卷更新日期:2023-09-08 类型:中考真卷
一、单选题
-
1. 计算 , 正确的结果是( )A、 B、 C、 D、2. 2023年5月21日,以“聚力新南通、奋进新时代”为主题的第五届通商大会暨全市民营经济发展大会召开,40个重大项目集中签约,计划总投资约元.将用科学记数法表示为( )A、 B、 C、 D、3. 如图所示的四个几何体中,俯视图是三角形的是( )A、
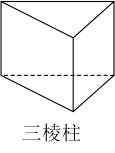 B、
B、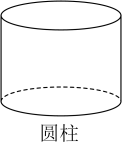 C、
C、 D、
D、 4. 如图,数轴上 , , , , 五个点分别表示数1,2,3,4,5,则表示数的点应在( )
4. 如图,数轴上 , , , , 五个点分别表示数1,2,3,4,5,则表示数的点应在( )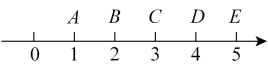 A、线段上 B、线段上 C、线段上 D、线段上5. 如图,中, , 顶点 , 分别在直线 , 上.若 , , 则的度数为( )
A、线段上 B、线段上 C、线段上 D、线段上5. 如图,中, , 顶点 , 分别在直线 , 上.若 , , 则的度数为( ) A、 B、 C、 D、6. 若 , 则的值为( )A、24 B、20 C、18 D、167. 如图,从航拍无人机看一栋楼顶部的仰角为 , 看这栋楼底部的俯角为 , 无人机与楼的水平距离为 , 则这栋楼的高度为( )
A、 B、 C、 D、6. 若 , 则的值为( )A、24 B、20 C、18 D、167. 如图,从航拍无人机看一栋楼顶部的仰角为 , 看这栋楼底部的俯角为 , 无人机与楼的水平距离为 , 则这栋楼的高度为( ) A、 B、 C、 D、8. 如图,四边形是矩形,分别以点 , 为圆心,线段 , 长为半径画弧,两弧相交于点 , 连接 , , . 若 , , 则的正切值为( )
A、 B、 C、 D、8. 如图,四边形是矩形,分别以点 , 为圆心,线段 , 长为半径画弧,两弧相交于点 , 连接 , , . 若 , , 则的正切值为( )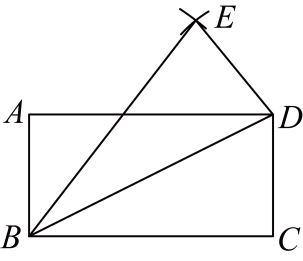 A、 B、 C、 D、9. 如图,中, , , . 点从点出发沿折线运动到点停止,过点作 , 垂足为 . 设点运动的路径长为 , 的面积为 , 若与的对应关系如图所示,则的值为( )
A、 B、 C、 D、9. 如图,中, , , . 点从点出发沿折线运动到点停止,过点作 , 垂足为 . 设点运动的路径长为 , 的面积为 , 若与的对应关系如图所示,则的值为( ) A、54 B、52 C、50 D、4810. 若实数 , , 满足 , , 则代数式的值可以是( )A、 B、 C、 D、
A、54 B、52 C、50 D、4810. 若实数 , , 满足 , , 则代数式的值可以是( )A、 B、 C、 D、二、填空题
-
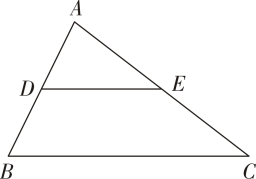
11. 计算: =.12. 分解因式: = .13. 在△ABC中(如图),点D、E分别为AB、AC的中点,则S△ADE:S△ABC= .
 14. 某型号汽车行驶时功率一定,行驶速度(单位:m/s)与所受阻力(单位:N)是反比例函数关系,其图象如图所示.若该型号汽车在某段公路上行驶时速度为 , 则所受阻力为 .
14. 某型号汽车行驶时功率一定,行驶速度(单位:m/s)与所受阻力(单位:N)是反比例函数关系,其图象如图所示.若该型号汽车在某段公路上行驶时速度为 , 则所受阻力为 . 15. 如图,是的直径,点 , 在上.若 , 则度.
15. 如图,是的直径,点 , 在上.若 , 则度. 16. 勾股数是指能成为直角三角形三条边长的三个正整数,世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》.现有勾股数a , b , c , 其中 , 均小于 , , , 是大于1的奇数,则(用含的式子表示).17. 已知一次函数 , 若对于范围内任意自变量的值,其对应的函数值都小于 , 则的取值范围是 .18. 如图,四边形的两条对角线 , 互相垂直, , , 则的最小值是 .
16. 勾股数是指能成为直角三角形三条边长的三个正整数,世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》.现有勾股数a , b , c , 其中 , 均小于 , , , 是大于1的奇数,则(用含的式子表示).17. 已知一次函数 , 若对于范围内任意自变量的值,其对应的函数值都小于 , 则的取值范围是 .18. 如图,四边形的两条对角线 , 互相垂直, , , 则的最小值是 .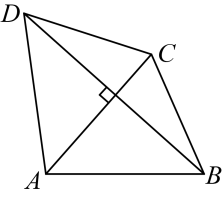
三、解答题
-
19.(1)、计算:(2)、解方程组:20. 某校开展以"筑梦天宫、探秘苍穹"为主题的航天知识竞赛,赛后在七、八年级各随机抽取20名学生的竞赛成绩,进行整理、分析,得出有关统计图表.
 (1)、若该校八年级共有300名学生参赛,估计优秀等次的约有人;(2)、你认为七、八年级中哪个年级学生的竞赛成绩更好些?请从两个方面说明理由.21. 如图,点 , 分别在 , 上, , , 相交于点 , .
(1)、若该校八年级共有300名学生参赛,估计优秀等次的约有人;(2)、你认为七、八年级中哪个年级学生的竞赛成绩更好些?请从两个方面说明理由.21. 如图,点 , 分别在 , 上, , , 相交于点 , .
求证: .
小虎同学的证明过程如下:
证明:∵ ,
∴ .
∵ ,
∴ . 第一步
又 , ,
∴第二步
∴第三步
(1)、小虎同学的证明过程中,第步出现错误;(2)、请写出正确的证明过程.22. 有同型号的 , 两把锁和同型号的 , , 三把钥匙,其中钥匙只能打开锁,钥匙只能打开锁,钥匙不能打开这两把锁.(1)、从三把钥匙中随机取出一把钥匙,取出钥匙的概率等于;(2)、从两把锁中随机取出一把锁,从三把钥匙中随机取出一把钥匙,求取出的钥匙恰好能打开取出的锁的概率.23. 如图,等腰三角形的顶角 , 和底边相切于点 , 并与两腰 , 分别相交于 , 两点,连接 , . (1)、求证:四边形是菱形;(2)、若的半径为2,求图中阴影部分的面积.24. 为推进全民健身设施建设,某体育中心准备改扩建一块运动场地.现有甲、乙两个工程队参与施工,具体信息如下:
(1)、求证:四边形是菱形;(2)、若的半径为2,求图中阴影部分的面积.24. 为推进全民健身设施建设,某体育中心准备改扩建一块运动场地.现有甲、乙两个工程队参与施工,具体信息如下:信息—
工程队
每天施工面积(单位:)
每天施工费用(单位:元)
甲
3600
乙
x
2200
信息二
甲工程队施工所需天数与乙工程队施工所需天数相等.
(1)、求x的值;(2)、该工程计划先由甲工程队单独施工若干天,再由乙工程队单独继续施工,两队共施工22天,且完成的施工面积不少于 . 该段时间内体育中心至少需要支付多少施工费用?25. 正方形中,点在边 , 上运动(不与正方形顶点重合).作射线 , 将射线绕点逆时针旋转45°,交射线于点 .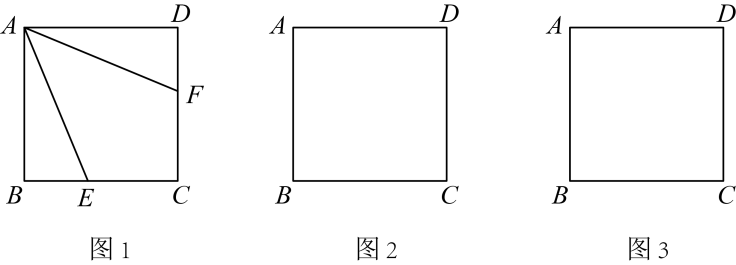 (1)、如图,点在边上, , 则图中与线段相等的线段是;(2)、过点作 , 垂足为 , 连接 , 求的度数;(3)、在(2)的条件下,当点在边延长线上且时,求的值.26. 定义:平面直角坐标系中,点 , 点 , 若 , , 其中为常数,且 , 则称点是点的“级变换点”.例如,点是点的“级变换点”.(1)、函数的图象上是否存在点的“级变换点”?若存在,求出的值;若不存在,说明理由;(2)、点与其“级变换点” 分别在直线 , 上,在 , 上分别取点 , . 若 , 求证:;(3)、关于x的二次函数的图象上恰有两个点,这两个点的“1级变换点”都在直线上,求n的取值范围.
(1)、如图,点在边上, , 则图中与线段相等的线段是;(2)、过点作 , 垂足为 , 连接 , 求的度数;(3)、在(2)的条件下,当点在边延长线上且时,求的值.26. 定义:平面直角坐标系中,点 , 点 , 若 , , 其中为常数,且 , 则称点是点的“级变换点”.例如,点是点的“级变换点”.(1)、函数的图象上是否存在点的“级变换点”?若存在,求出的值;若不存在,说明理由;(2)、点与其“级变换点” 分别在直线 , 上,在 , 上分别取点 , . 若 , 求证:;(3)、关于x的二次函数的图象上恰有两个点,这两个点的“1级变换点”都在直线上,求n的取值范围.