备战2024年中考数学细点逐一突破真题训练第10章尺规作图设计、命题
试卷更新日期:2023-09-08 类型:一轮复习
一、命题
-
1. 下列句子中,属于命题的是( )A、直线和垂直吗? B、过线段的中点作的垂线 C、同旁内角不互补,两直线不平行 D、已知 , 求的值2. 下列命题是真命题的是( )A、的两边为3,4,则斜边上的高是 B、角是轴对称图形,它的平分线所在的直线就是它的对称轴 C、三角形三个内角平分线的交点到三个顶点的距离相等 D、对角线互相垂直平分的四边形是正方形3. 下列命题中,假命题的是( )A、对角线互相垂直的平行四边形是菱形 B、对角线互相垂直的梯形是等腰梯形 C、对角线平分一组对角的平行四边形是菱形 D、对角线平分一组对角的矩形是正方形4. 把命题“对顶角相等”改写成“如果……,那么……”的形式为 .5. 命题“内错角相等”的题设是 , 结论是 .6. 命题“如果 , 那么”的逆命题为 .7. 下列命题中,正确的是( )A、位似图形一定是相似图形 B、平分弦的直径垂直于这条弦 C、方程有两个相等的实数根 D、反比例函数在每一象限内,y随x的增大而减小8. 下列命题中,是真命题的有( ).
①全等三角形的对应边相等;②有两个角为的三角形一定是等边三角形;③两条直线被第三条直线所截,内错角相等;④等腰三角形的角平分线和中线相互重合.
A、1个 B、2个 C、3个 D、4个9. 下列说法正确的是( )A、为了加强“五项管理”,要了解某市中学生的睡眠时间,采用全面调查 B、打开电视机,它正在播广告是必然事件 C、一组数据“5,4,6,2,7,4,3”的众数是4,中位数是2 D、甲、乙两名同学5次数学测试的平均数都是92分,方差分别为 , , 由此可以判断甲的数学成绩比乙的稳定二、尺规作图设计-与平面直角坐标系相关(对称、平移、旋转,位似)
-
10. 在平面直角坐标系中,的三个顶点在格点上(每个方格的边长均为1个单位长度).
 (1)、请画出关于轴对称的图形;(2)、将绕点逆时针旋转90°,画出旋转后得到的;(3)、在轴上找一点 , 使的值最小(不写作法,保留作图痕迹).11. 如图,直线垂足为O , 请按要求画图.
(1)、请画出关于轴对称的图形;(2)、将绕点逆时针旋转90°,画出旋转后得到的;(3)、在轴上找一点 , 使的值最小(不写作法,保留作图痕迹).11. 如图,直线垂足为O , 请按要求画图.
⑴点P在射线上,画出点P到直线a的最短路径 .
⑵画出表示南偏西方向的射线 .
12. 如图,在平面直角坐标系中,每个小正方格的边长都是1个单位长度,已知\的顶点坐标为 .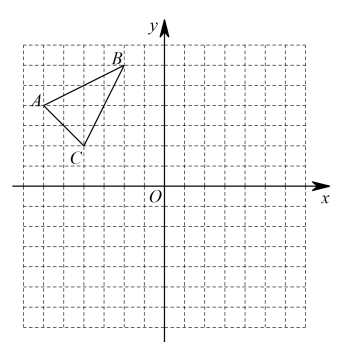
⑴画出沿着x轴向右平移5个单位长度得到的;
⑵以原点O为位似中心,将△ABC缩小为原来的 ,请在位似中心同侧画出缩小后的△A2B2C2 .⑶直接写出线段C1C2的长.
13. 如图,在平面直角坐标系中,已知的三个顶点坐标分别是 , . (1)、将向上平移4个单位,再向右平移1个单位,得到 , 请画出 .(2)、请画出关于轴对称的 .(3)、将着原点顺时针旋转 , 得到 , 求线段在旋转过程中扫过的面积(结果保留).14. 如图是由小正方形组成的12×11网格,每个小正方形的顶点叫作格点,过格点A,B,C的圆交于点F,点G在DE上,其中D,G是格点.仅用无刻度的直尺在给定网格中按要求完成画图,画图过程用虚线表示.
(1)、将向上平移4个单位,再向右平移1个单位,得到 , 请画出 .(2)、请画出关于轴对称的 .(3)、将着原点顺时针旋转 , 得到 , 求线段在旋转过程中扫过的面积(结果保留).14. 如图是由小正方形组成的12×11网格,每个小正方形的顶点叫作格点,过格点A,B,C的圆交于点F,点G在DE上,其中D,G是格点.仅用无刻度的直尺在给定网格中按要求完成画图,画图过程用虚线表示.
⑴在AD的下方画出正方形ADMN;
⑵画出圆心O;
⑶画出的中点P;
⑷画出线段AE绕点A逆时针旋转90°后的对应线段AQ.
三、尺规作图设计-与网格相关(形状大小、面积、长度值)
-
15. 下图各正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点都称为格点.
 (1)、在图①中,画出一条以格点为端点,长度为的线段 .(2)、在图②中,以格点为顶点,画出三边长分别为3, , 的三角形.16. 如图,正方形网格图中,每个小正方形的边长都是1.
(1)、在图①中,画出一条以格点为端点,长度为的线段 .(2)、在图②中,以格点为顶点,画出三边长分别为3, , 的三角形.16. 如图,正方形网格图中,每个小正方形的边长都是1. (1)、在图中分别画出线段 , , ;(2)、判断以 , , 三条线段为边能否构成直角三角形,并说明理由.17. 图①.图四、图③都是的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点叫做格点,故段的端点都在格点上.在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写画法.
(1)、在图中分别画出线段 , , ;(2)、判断以 , , 三条线段为边能否构成直角三角形,并说明理由.17. 图①.图四、图③都是的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点叫做格点,故段的端点都在格点上.在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写画法. (1)、在图①中画 , 使的面积是10;(2)、在图②中画四边形 , 使四边形是轴对称图形;(3)、在图③中的线段上找一点P , 使 .18. 图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均在格点上,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,不要求写出画法.
(1)、在图①中画 , 使的面积是10;(2)、在图②中画四边形 , 使四边形是轴对称图形;(3)、在图③中的线段上找一点P , 使 .18. 图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均在格点上,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,不要求写出画法. (1)、在图①中作的角平分线 .(2)、在图②、图③中,过点C作一条直线 , 使点A、B到直线的距离相等,图②、图③所画直线不相同.19. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,的顶点均在格点上.只用无刻度的直尺,分别在给定的网格中按下列要求作图,保留作图痕迹.
(1)、在图①中作的角平分线 .(2)、在图②、图③中,过点C作一条直线 , 使点A、B到直线的距离相等,图②、图③所画直线不相同.19. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,的顶点均在格点上.只用无刻度的直尺,分别在给定的网格中按下列要求作图,保留作图痕迹.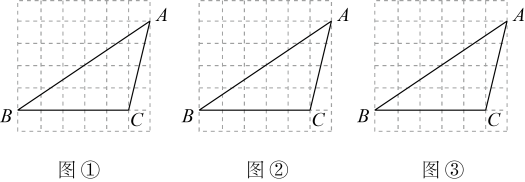 (1)、在图①中,作的中线 .(2)、在图②中,在边上找一点E,连结 , 使 .(3)、在图③中,在边上找一点F,连结BF,使的面积为 .20. 如图,图①、图②均是的正方形网格,每个小正方形的边长均为 , 每个小正方形的顶点称为格点,点、、均为格点只用无刻度的直尺,按下列要求作图:
(1)、在图①中,作的中线 .(2)、在图②中,在边上找一点E,连结 , 使 .(3)、在图③中,在边上找一点F,连结BF,使的面积为 .20. 如图,图①、图②均是的正方形网格,每个小正方形的边长均为 , 每个小正方形的顶点称为格点,点、、均为格点只用无刻度的直尺,按下列要求作图: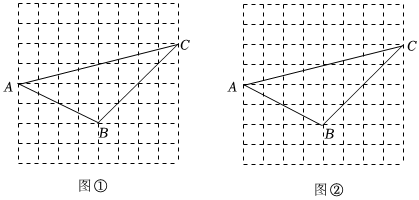 (1)、在图①中,作的边上的高;(2)、在图②中,过点作直线 , 使得直线平分的面积.21. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点.的顶点均在格点,点D为上一格点,点E为上任一点,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留作图痕迹.
(1)、在图①中,作的边上的高;(2)、在图②中,过点作直线 , 使得直线平分的面积.21. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点.的顶点均在格点,点D为上一格点,点E为上任一点,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留作图痕迹.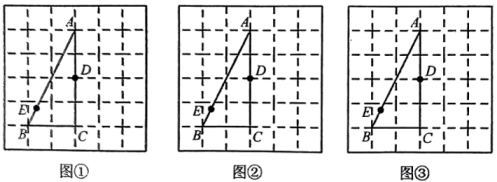 (1)、在图①中画的中位线 , 使点F在边上.(2)、在图②中画以为对角线的 .(3)、在图③中作射线 , 在其上找到一点H,使 .22. 如图,在的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点、、均为格点,只用无刻度的直尺,分别在给定的网格中找一格点满足下列要求:
(1)、在图①中画的中位线 , 使点F在边上.(2)、在图②中画以为对角线的 .(3)、在图③中作射线 , 在其上找到一点H,使 .22. 如图,在的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点、、均为格点,只用无刻度的直尺,分别在给定的网格中找一格点满足下列要求: (1)、在图①中,作格点 , 并连结、、 , 使 .(2)、在图②中,作格点 , 并连结、使 .(3)、在图③中,作格点 , 并连结、 , 使 .23. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,正方形四个顶点都是格点,是上的格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)、在图①中,作格点 , 并连结、、 , 使 .(2)、在图②中,作格点 , 并连结、使 .(3)、在图③中,作格点 , 并连结、 , 使 .23. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,正方形四个顶点都是格点,是上的格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.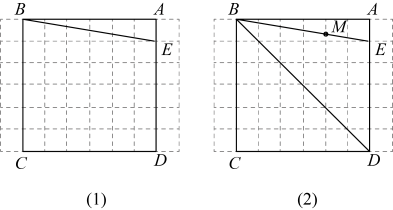 (1)、在图(1)中,先将线段绕点顺时针旋转 , 画对应线段 , 再在上画点 , 并连接 , 使;(2)、在图(2)中,是与网格线的交点,先画点关于的对称点 , 再在上画点 , 并连接 , 使 .
(1)、在图(1)中,先将线段绕点顺时针旋转 , 画对应线段 , 再在上画点 , 并连接 , 使;(2)、在图(2)中,是与网格线的交点,先画点关于的对称点 , 再在上画点 , 并连接 , 使 .四、尺规作图设计-综合类型
-
24. 下面是“作已知直角三角形的外接圆”的尺规作图过程:
已知:如图1,在中, .
求作:的外接圆.
作法:如图2.
(1)分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于P,Q两点;
(2)作直线 , 交于点O;
(3)以O为圆心,为半径作 , 即为所求作的圆.
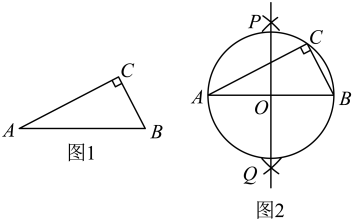
下列不属于该尺规作图依据的是( )
A、两点确定一条直线 B、直角三角形斜边上的中线等于斜边的一半 C、与线段两个端点距离相等的点在这条线段的垂直平分线上 D、线段垂直平分线上的点与这条线段两个端点的距离相等25.(1)、已知线段 , 求作 , 使得;(请用尺规作图,保留作图痕迹,不写作法.) (2)、求证:直角三角形斜边上的中线等于斜边的一半.(请借助上一小题所作图形,在完善的基础上,写出已知、求证与证明.)26. 已知:线段 , , , .
(2)、求证:直角三角形斜边上的中线等于斜边的一半.(请借助上一小题所作图形,在完善的基础上,写出已知、求证与证明.)26. 已知:线段 , , , .
求作:(要求:仅用无刻度的直尺和圆规作图,不写作法,保留作图痕迹)
(1)、线段;(2)、 .27. 如图所示,请用尺规作图法,在矩形的边上确定一点 , 使得 . 28. 下面是小明设计的“作菱形”的尺规作图过程.
28. 下面是小明设计的“作菱形”的尺规作图过程.求作:菱形 .
作法:①作线段;
②作线段的垂直平分线l,交于点O;
③在直线l上取点B,以O为圆心,长为半径画弧,交直线l于点D(点B与点D不重合);
④连接 .
所以四边形为所求作的菱形.

根据小明设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.证明:∵ , ,
∴四边形为 ▲ .
∵ ▲ ,
∴四边形为菱形( )(填推理的依据).

