备战2024年中考数学细点逐一突破真题训练第9章二次函数的实际应用-在线组卷题库

1. “端午节”吃粽子是中国传统习俗，在“端午节”来临前，某超市购进一种品牌粽子，每盒进价是40元，并规定每盒售价不得少于50元，日销售量不低于350盒，根据以往销售经验发现，当每盒售价定为50元时，日销售量为500盒，每盒售价每提高1元，日销售量减少10盒，设每盒售价为x元，日销售量为p盒．

(1)、当 $x = 60$ 时， $p =$ ；

(2)、当每盒售价定为多少元时，日销售利润W（元）最大？最大利润是多少？

(3)、小强说：“当日销售利润最大时，日销售额不是最大，”小红说：“当日销售利润不低于8000元时，每盒售价x的范围为 $60 \leq x \leq 80$ ． ”你认为他们的说法正确吗？若正确，请说明理由；若不正确，请直接写出正确的结论．

查看试题解析
2. 某商店决定购进A，B两种纪念品进行销售．已知每件A种纪念品比每件B种纪念品的进价高30元．用1000元购进A种纪念品的数量和用400元购进B种纪念品的数量相同．

(1)、求A，B两种纪念品每件的进价分别是多少元？

(2)、该商场通过市场调查，整理出A型纪念品的售价与数量的关系如表，

售价x（元/件）

$50 \leq x \leq 60$

$60 ＜ x \leq 80$

销售量（件）

100

$400 - 5 x$

①当x为何值时，售出A纪念品所获利润最大，最大利润为多少？

②该商场购进A，B型纪念品共200件，其中A型纪念品的件数少于B型纪念品的件数，但不少于60件．若B型纪念品的售价为30元/件时，求商场将A，B型纪念品均全部售出后获得的最大利润．

查看试题解析
3. 某工厂计划从A，B两种产品中选择一种生产并销售，每日产销x件．已知A产品成本价m元/件（m为常数，且 $4 \leq m \leq 6$ ，售价8元/件，每日最多产销500件，同时每日共支付专利费30元；B产品成本价12元/件，售价20元/件，每日最多产销300件，同时每日支付专利费y元，y（元）与每日产销x（件）满足关系式 $y = 80 + 0.01 x^{2 .}$

(1)、若产销A，B两种产品的日利润分别为 $w_{1}$ 元， $w_{2}$ 元，请分别写出 $w_{1}$ ， $w_{2}$ 与x的函数关系式，并写出x的取值范围；

(2)、分别求出产销A，B两种产品的最大日利润．（A产品的最大日利润用含m的代数式表示）

(3)、为获得最大日利润，该工厂应该选择产销哪种产品？并说明理由．【利润 $=$ （售价 $-$ 成本） $\times$ 产销数量 $-$ 专利费】

查看试题解析
4. 综合与实践
问题情境
小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉，为了确定售价，小莹帮妈妈调查了附近A，B，C，D，E五家花卉店近期该种盆栽花卉的售价与日销售量情况，记录如下：

售价（元/盆）
日销售量（盆）
A
20
50
B
30
30
C
18
54
D
22
46
E
26
38

(1)、数据整理
请将以上调查数据按照一定顺序重新整理，填写在下表中：

售价（元/盆）

日销售量（盆）

(2)、模型建立
分析数据的变化规律，找出日销售量与售价间的关系；

(3)、拓广应用
根据以上信息，小莹妈妈在销售该种花卉中，
①要想每天获得400元的利润，应如何定价？
②售价定为多少时，每天能够获得最大利润？

查看试题解析

5. 某景区旅游商店以 $20$ 元 $/ k g$ 的价格采购一款旅游食品加工后出售，销售价格不低于 $22$ 元 $/ g$ ，不高于 $45$ 元 $g$ ，经市场调查发现每天的销售量 $y (k g)$ 与销售价格 $x$ （元 $g$ ）之间的函数关系如图所示．

(1)、求 $y$ 关于 $x$ 的函数表达式：

(2)、当销售价格定为多少时，该商店销售这款食品每天获得的销售利润最大？最大销售利润是多少？【销售利润=（销售价格一采购价格）×销售量】

查看试题解析
6. 加强劳动教育，落实五育并举．孝礼中学在当地政府的支持下，建成了一处劳动实践基地.2023年计划将其中 $1000 m^{2}$ 的土地全部种植甲乙两种蔬菜．经调查发现：甲种蔬菜种植成本y（单位；元/ $m^{2}$ ）与其种植面积x（单位： $m^{2}$ ）的函数关系如图所示，其中 $200 \leq x \leq 700$ ；乙种蔬菜的种植成本为50元/ $m^{2}$ ．

(1)、当 $x =$ $m^{2}$ 时， $y = 35$ 元/ $m^{2}$ ；

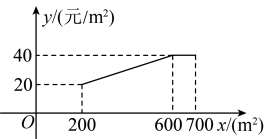(2)、设2023年甲乙两种蔬菜总种植成本为W元，如何分配两种蔬菜的种植面积，使W最小？

(3)、学校计划今后每年在这 $1000 m^{2}$ 土地上，均按（2）中方案种植蔬菜，因技术改进，预计种植成本逐年下降，若甲种蔬菜种植成本平均每年下降 $10 %$ ，乙种蔬菜种植成本平均每年下降 $a %$ ，当a为何值时，2025年的总种植成本为 $28920$ 元？

查看试题解析
7. 为了振兴乡村经济，增加村民收入，某村委会干部带领村民在网上直播推销农产品，在试销售的30天中，第x天（ $1 \leq x \leq 30$ 且x为整数）的售价p（元/千克）与x的函数关系式 $p = {\begin{array}{l} m x + n (1 \leq x < 20) \\ 30 (20 \leq x \leq 30) \end{array}$ （且x为整数），销量q（千克）与x的函数关系式为 $q = x + 10$ ，已知第5天售价为50元/千克，第10天售价为40元/千克，设第x天的销售额为W元

(1)、 $m =$ ， $n =$ ；

(2)、求第x天的销售额W元与x之间的函数关系式；

(3)、在试销售的30天中，销售额超过1000元的共有多少天？

查看试题解析
8. 某公司调研了历年市场行情和生产情况以后，对今年某种商品的销售价格和成本价格进行预测，提供了两方面的信息，如图所示．图1的图象是线段，图2的图象是部分抛物线．

(1)、在3月份和6月份出售这种商品，哪个月商品的单件利润更大？

(2)、分别求出线段和抛物线的解析式，即可得出单件利润关于t的二次函数解析式，再求出函数的最值即可．

查看试题解析

9. 如图，一名学生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是 $y = - \frac{1}{12} (x - 10) (x + 4)$ ，则铅球推出的距离 $O A =$ m．

查看试题解析
10. 一次足球训练中，小明从球门正前方8m的 $A$ 处射门，球射向球门的路线呈抛物线.当球飞行的水平距离为6m时，球达到最高点，此时球离地面3m.已知球门高OB为2.44m，现以 $O$ 为原点建立如图所示直角坐标系.

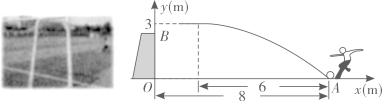(1)、求抛物线的函数表达式，并通过计算判断球能否射进球门（忽略其他因素）。

(2)、对本次训练进行分析，若射门路线的形状、最大高度均保持不变，则当时他应该带球向正后方移动多少米射门，才能让足球经过点 $O$ 正上方2.25m处?

查看试题解析
11. 某投球发射装置斜向上发射进行投球实验，球离地面的高度h（米）与球运行时间t（秒）之间满足函数关系式 $h = - 5 t^{2} + m t + n$ ，该装置的发射点离地面10米，球筐中心点离地面35米．如图，若某次投球正好中心入筐，球到达球筐中心点所需时间为5秒，那么这次投球过程中球离地面的高度h（米）与球运行时间t（秒）之间满足的函数关系式为．（不要求写自变量的取值范围）；我们把球在每2秒内运行的最高点离地面的高度与最低点离地面的高度的差称为“投射矩”，常用字母“L”表示．那么在这次投球过程中，球入筺前L的取值范围是．

查看试题解析
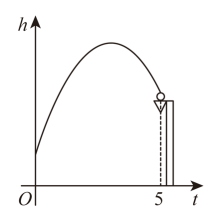12. 如图，在水平地面点A处有一网球发射器向空中发射网球，网球在地面上的落点为B，网球的飞行路线是一条抛物线，已知 $A B = 4$ 米， $A C = 3$ 米．网球飞行的最大高度 $O M = 3$ 米．

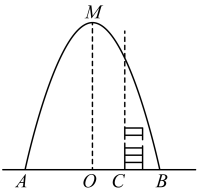(1)、建立合适的平面直角坐标系，求抛物线的函数表达式．

(2)、小明在直线 $A B$ 上，点C右侧竖直向上摆放若干个无盖的直径为0.5米，高为0.3米的圆柱形桶（网球的体积和圆柱形桶的厚度忽略不计），若要是网球刚好落入桶内，至少摆放多少个圆柱形桶？

查看试题解析
13. 北京冬奥会的召开激起了人们对冰雪运动的极大热情，如图是某小型跳台滑雪训练场的横截面示意图，取某一位置的水平线为 $x$ 轴，过跳台终点 $A$ 作水平线的垂线为 $y$ 轴，建立平面直角坐标系，图中的抛物线 $C_{1}$ ： $y = - \frac{1}{12} x^{2} + \frac{4}{3} x + \frac{4}{3}$ 近似表示滑雪场地上的一座小山坡，某滑雪爱好者小张从点 $O$ 正上方 $A$ 点滑出，滑出后沿一段抛物线 $C_{2}$ ： $y = - \frac{1}{8} x^{2} + b x + c$ 运动．

(1)、当小张滑到离 $A$ 处的水平距离为 $6$ 米时，其滑行高度最大，为 $\frac{17}{2}$ 米，直接写出 $b$ ， $c$ 的值；

(2)、在（1）的条件下，当小张滑出后离 $A$ 的水平距离为多少米时，他滑行高度与小山坡的竖直距离为 $\frac{4}{3}$ 米？

(3)、小张从 $A$ 点滑出，滑行的高度恰好在坡顶正上方时，与坡顶距离不低于3米，求此时 $b$ ， $c$ 的值或取值范围．

查看试题解析
14. 小林同学不仅是一名羽毛球运动爱好者，还喜欢运用数学知识对羽毛球比赛进行技术分析，下面是他对击球线路的分析．
如图，在平面直角坐标系中，点A，C在x轴上，球网AB与y轴的水平距离 $O A = 3$ m， $C A = 2$ m，击球点P在y轴上．若选择扣球，羽毛球的飞行高度y（m）与水平距离x（m）近似满足一次函数关系 $y = - 0.4 x + 2.8$ ；若选择吊球，羽毛球的飞行高度y（m）与水平距离x（m）近似满足二次函数关系 $y = a {(x - 1)}^{2} + 3.2$ ．

(1)、求点P的坐标和a的值．

(2)、小林分析发现，上面两种击球方式均能使球过网．要使球的落地点到C点的距离更近，请通过计算判断应选择哪种击球方式．

查看试题解析

15. 要修一个圆形喷水池，在池中心竖直安装一根水管，水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为 $1 m$ 处达到最高，高度为 $3 m$ ，水柱落地处离池中心 $3 m$ ，水管长度应为．

查看试题解析
16. 一名运动员在 $10 m$ 高的跳台进行跳水，身体（看成一点）在空中的运动轨迹是一条抛物线，运动员离水面 $O B$ 的高度 $y (m)$ 与离起跳点A的水平距离 $x (m)$ 之间的函数关系如图所示，运动员离起跳点A的水平距离为 $1 m$ 时达到最高点，当运动员离起跳点A的水平距离为 $3 m$ 时离水面的距离为 $7 m$ ．

(1)、求y关于x的函数表达式；

(2)、求运动员从起跳点到入水点的水平距离 $O B$ 的长．

查看试题解析
17. 如图①，是一座抛物线型拱桥，小星学习二次函数后，受到该图启示设计了一建筑物造型，它的截面图是抛物线的一部分（如图②所示），抛物线的顶点在 $C$ 处，对称轴 $O C$ 与水平线 $O A$ 垂直， $O C = 9$ ，点 $A$ 在抛物线上，且点 $A$ 到对称轴的距离 $O A = 3$ ，点 $B$ 在抛物线上，点 $B$ 到对称轴的距离是1．

(1)、求抛物线的表达式；

(2)、如图②，为更加稳固，小星想在 $O C$ 上找一点 $P$ ，加装拉杆 $P A ， P B$ ，同时使拉杆的长度之和最短，请你帮小星找到点 $P$ 的位置并求出坐标；

(3)、为了造型更加美观，小星重新设计抛物线，其表达式为 $y = - x^{2} + 2 b x + b - 1 (b > 0)$ ，当 $4 \leq x \leq 6$ 时，函数 $y$ 的值总大于等于9．求 $b$ 的取值范围．

查看试题解析
18. 城建部门计划修建一条喷泉步行通道．图1是项目俯视示意图．步行通道的一侧是一排垂直于路面的柱形喷水装置，另一侧是方形水池．图2是主视示意图．喷水装置 $O A$ 的高度是2米，水流从喷头A处喷出后呈抛物线路径落入水池内，当水流在与喷头水平距离为2米时达到最高点B，此时距路面的最大高度为3.6米．为避免溅起的水雾影响通道上的行人，计划安装一个透明的倾斜防水罩，防水罩的一端固定在喷水装置上的点 $M$ 处，另一端与路面的垂直高度 $N C$ 为1.8米，且与喷泉水流的水平距离 $N D$ 为0.3米．点 $C$ 到水池外壁的水平距离 $C E = 0.6$ 米，求步行通道的宽 $O E$ ．（结果精确到0.1米）参考数据： $\sqrt{2} \approx 1.41$

查看试题解析
19. 某公园修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安装一个可调节角度的喷水头，从喷水头喷出的水柱形状是一条抛物线．建立如图所示的平面直角坐标系，抛物线形水柱的竖直高度 $y$ （单位：m）与到池中心的水平距离 $x$ （单位：m）满足的关系式近似为 $y = a {(x - h)}^{2} + k$ （ $a < 0$ ）．

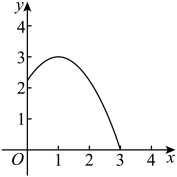(1)、在某次安装调试过程中，测得 $x$ 与 $y$ 的部分对应值如下表：
水平距离 $x / m$
0
0.5
1
1.5
2
2.5
3
竖直高度 $y / m$
2.25
2.8125
3
2.8125
2.25
1.3125
0
根据表格中的数据，解答下列问题：
①水管的长度是m；
②求出 $y$ 与 $x$ 满足的函数解析式 $y = a {(x - h)}^{2} + k$ （ $a < 0$ ）；

(2)、安装工人在上述基础上进行了下面两种调试：
①不改变喷水头的角度，将水管长度增加1m，水柱落地时与池中心的距离为 $d_{1}$ ；
②不改变水管的长度，调节喷水头的角度，使得水柱满足 $y = - 0.6 {(x - 1.5)}^{2} + 3.6$ ，水柱落地时与池中心的距离为 $d_{2}$ ．则比较 $d_{1}$ 与 $d_{2}$ 的大小关系是： $d_{1}$ $d_{2}$ （填“ $>$ ”或“ $=$ ”或“ $<$ ”）

查看试题解析
20. 随着自动化设备的普及，公园中引入了自动喷灌系统.图1是某公园内的一个可垂直升降的草坪喷灌器，从喷水口喷出的水柱均为形状相同的抛物线，图2是该喷灌器喷水时的截面示意图.

(1)、喷水口A离地高度为 $0.35 m$ ，喷出的水柱在离喷水口水平距离为 $3 m$ 处达到最高，高度为 $0.8 m$ ，且水柱刚好落在公园围栏和地面的交界B处.
①在图2中建立合适的平面直角坐标系，并求出抛物线的解析式；
②求喷灌器底端O到点B的距离；

(2)、现准备在公园内沿围栏建花坛，花坛的截面示意图为矩形 $B C D E$ （如图3），其中高 $C D$ 为 $0.5 m$ .宽 $C B$ 为 $0.8 m$ .为达到给花坛喷灌的效果，需将喷水口A向上升高 $h m$ ，使水柱落在花坛的上方 $D E$ 边上，求h的取值范围.

查看试题解析

21. 某市新建一座景观桥．如图，桥的拱肋 $A D B$ 可视为抛物线的一部分，桥面 $A B$ 可视为水平线段，桥面与拱肋用垂直于桥面的杆状景观灯连接，拱肋的跨度 $A B$ 为40米，桥拱的最大高度 $C D$ 为16米（不考虑灯杆和拱肋的粗细），则与 $C D$ 的距离为5米的景观灯杆 $M N$ 的高度为（）

A、13米 B、14米 C、15米 D、16米

查看试题解析
22. 如图所示，拱桥的形状是抛物线，其函数关系式为 $y = - \frac{1}{16} x^{2}$ ，当水面离桥顶的高度 $O H$ 为 $4 m$ 时，水面的宽度AB为m.

查看试题解析
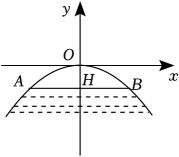23. 某校想将新建图书楼的正门设计为一个抛物线型门，并要求所设计的拱门的跨度与拱高之积为 $48 m^{3}$ ，还要兼顾美观、大方，和谐、通畅等因素，设计部门按要求价出了两个设计方案 $.$ 现把这两个方案中的拱门图形放入平面直角坐标系中，如图所示：
方案一，抛物线型拱门的跨度 $O N = 12 m$ ，拱高 $P E = 4 m .$ 其中，点 $N$ 在 $x$ 轴上， $P E ⊥ O N$ ， $O E = E N$ ．

方案二，抛物线型拱门的跨度 $O N' = 8 m$ ，拱高 $P' E' = 6 m .$ 其中，点 $N'$ 在 $x$ 轴上， $P' E' ⊥ O' N'$ ， $O' E' = E' N'$ ．

要在拱门中设置高为 $3 m$ 的矩形框架，其面积越大越好 $($ 框架的粗细忽略不计 $) .$ 方案一中，矩形框架 $A B C D$ 的面积记为 $S_{1}$ ，点 $A$ 、 $D$ 在抛物线上，边 $B C$ 在 $O N$ 上；方案二中，矩形框架 $A' B' C' D'$ 的面积记为 $S_{2}$ ，点 $A'$ ， $D'$ 在抛物线上，边 $B' C'$ 在 $O N'$ 上 $.$ 现知，小华已正确求出方案二中，当 $A' B' = 3 m$ 时， $S_{2} = 12 \sqrt{2} m^{2}$ ，请你根据以上提供的相关信息，解答下列问题：

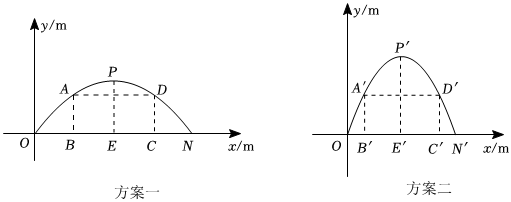(1)、求方案一中抛物线的函数表达式；

(2)、在方案一中，当 $A B = 3 m$ 时，求矩形框架 $A B C D$ 的面积 $S_{1}$ 并比较 $S_{1}$ ， $S_{2}$ 的大小．

查看试题解析
24. 如图1，有一座抛物线形拱桥，某正常水位时，桥下的水面宽20米，拱顶到水面的距离为6米，到桥面的距离为4米，相邻两支柱间的距离均为5米，建立直角坐标系如图2.

(1)、求抛物线的函数表达式.

(2)、求支柱 $M N$ 的长度.

(3)、随着水位的上升，桥下水面的宽度逐渐减小.一艘货船在水面上的部分的横截面是边长为5米的正方形，当水位上升0.75米时，这艘货船能否顺利通过拱桥？请说说你的理由.

查看试题解析
25. 按要求解答

(1)、某市计划修建一条隧道，已知隧道全长2400米，一工程队在修了1400米后，加快了工作进度，每天比原计划多修5米，结果提前10天完成，求原计划每天修多长？

(2)、隧道建成后的截面图如图所示，它可以抽象成如图所示的抛物线．已知两个车道宽度 $O C = O D = 4$ 米，人行道地基AC，BD宽均为2米，拱高 $O M = 10.8$ 米．建立如图所示的直角坐标系．
①此抛物线的函数表达式为 ▲ ．（函数表达式用一般式表示）

②按规定，车顶部与隧道顶部在竖直方向上的高度差至少0.5米，则此隧道限高 ▲ 米．

③已知人行道台阶 $C E ， D F$ 高均为0.3米，按照国家标准，人行道宽度不得低于1.25米，该隧道的人行道宽度设计是否达标？说明理由．

+

查看试题解析
26. 蔬菜大棚是一种具有出色的保温性能的框架覆膜结构，它的出现使得人们可以吃到反季节蔬菜．一般蔬菜大棚使用竹结构或者钢结构的骨架，上面覆上一层或多层保温塑料膜，这样就形成了一个温室空间．如图，某个温室大棚的横截面可以看作矩形ABCD和抛物线AED构成，其中AB=3m，BC=4m，取BC中点O，过点O作线段BC的垂直平分线OE交抛物线AED于点E，若以O点为原点，BC所在直线为x轴，OE为y轴建立如图所示平面直角坐标系．

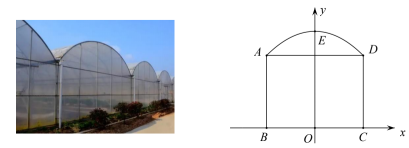
请回答下列问题：

(1)、如图，抛物线 $A E D$ 的顶点 $E (0 ， 4)$ ，求抛物线的解析式；

(2)、如图，为了保证蔬菜大棚的通风性，该大棚要安装两个正方形孔的排气装置 $L F G T$ ， $S M N R$ ，若 $F L = N R = 0.75 m$ ，求两个正方形装置的间距 $G M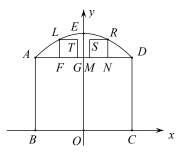$ 的长；

(3)、如图，在某一时刻，太阳光线透过A点恰好照射到C点，此时大棚截面的阴影为 $B K$ ，求 $B K$ 的长．

查看试题解析

27. 某建筑物的窗户如图所示，上半部分 $△ A B C$ 是等腰三角形， $A B = A C$ ， $A F ： B F = 3 ： 4$ ，点 $G$ 、 $H$ 、 $F$ 分别是边 $A B$ 、 $A C$ 、 $B C$ 的中点；下半部分四边形 $B C D E$ 是矩形， $B E ∥ I J ∥ M N ∥ C D$ ，制造窗户框的材料总长为16米（图中所有黑线的长度和），设 $B F = x$ 米， $B E = y$ 米．

(1)、求 $y$ 与 $x$ 之间的函数关系式，并求出自变量 $x$ 的取值范围；

(2)、当 $x$ 为多少时，窗户透过的光线最多（窗户的面积最大），并计算窗户的最大面积．

查看试题解析

28. 为响应荆州市“创建全国文明城市”号召，某单位不断美化环境，拟在一块矩形空地上修建绿色植物园，其中一边靠墙，可利用的墙长不超过18m，另外三边由36m长的栅栏围成．设矩形ABCD空地中，垂直于墙的边AB=xm，面积为ym²（如图）．

(1)、求y与x之间的函数关系式，并写出自变量x的取值范围；

(2)、若矩形空地的面积为160m² ，求x的值；

(3)、若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵（每种植物的单价和每棵栽种的合理用地面积如下表）．问丙种植物最多可以购买多少棵？此时，这批植物可以全部栽种到这块空地上吗？请说明理由．

	甲	乙	丙
单价（元/棵）	14	16	28
合理用地（m²/棵）	0.4	1	0.4

查看试题解析

29. 如图，计划利用长为a米的篱笆，再借助外墙围成一个矩形栅栏，设矩形 $A B C D$ 的边 $A B$ 长为x米，面积为y平方米.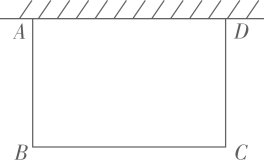

(1)、若 $a = 80$ ，墙长为50米，求出y与x之间的关系，并指出x的取值范围；

(2)、在（1）的条件下，矩形 $A B C D$ 的面积能达到800平方米吗？说明理由；

(3)、当x与a满足什么关系时，栅栏围出的面积最大？最大值是多少？

查看试题解析

备战2024年中考数学细点逐一突破真题训练第9章二次函数的实际应用

一、销售利润问题-常规题型

二、销售利润问题-与分段函数结合

三、抛球问题

四、喷泉问题

五、拱桥问题

六、多边形面积问题

售价x（元/件）	$50 \leq x \leq 60$	$60 ＜ x \leq 80$
销售量（件）	100	$400 - 5 x$

	售价（元/盆）	日销售量（盆）
A	20	50
B	30	30
C	18	54
D	22	46
E	26	38

水平距离 $x / m$	0	0.5	1	1.5	2	2.5	3
竖直高度 $y / m$	2.25	2.8125	3	2.8125	2.25	1.3125	0