江苏省苏州市苏州工业园区2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-09-07 类型:期末考试
一、单选题
-
1. 园区某校开展了“我为苏州园林设计”项目学习活动.如图是同学们设计的四个图案,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组二次根式中,是同类二次根式的是( )A、与 B、与 C、与 D、与3. 若点、都在反比例函数的图象上,则与的大小关系是( )A、 B、 C、 D、无法确定4. 下列事件中,属于不可能事件的是( )A、经过红绿灯路口,遇到绿灯 B、从一个只装有白球和红球的袋中摸球,摸出黄球 C、班里的两名同学,他们的生日是同一天 D、射击运动员射击一次,命中靶心5. 秦兵马俑的发现被誉为“世界第八大奇迹”,兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比为 , 下列各数中最接近于的是( )A、 B、 C、 D、6. 《姑苏繁华图》是清代苏州籍宫廷画家徐扬的作品,全长 , 反映的是当时苏州“商贾辐辏,百货骈阗”的市井风情.如图,已知局部临摹画面装裱前是一个长为 , 宽为的矩形,装裱后的长与宽的比是 , 且四周边衬的宽度相等.设边衬的宽度为x(m),根据题意可列方程( )
2. 下列各组二次根式中,是同类二次根式的是( )A、与 B、与 C、与 D、与3. 若点、都在反比例函数的图象上,则与的大小关系是( )A、 B、 C、 D、无法确定4. 下列事件中,属于不可能事件的是( )A、经过红绿灯路口,遇到绿灯 B、从一个只装有白球和红球的袋中摸球,摸出黄球 C、班里的两名同学,他们的生日是同一天 D、射击运动员射击一次,命中靶心5. 秦兵马俑的发现被誉为“世界第八大奇迹”,兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比为 , 下列各数中最接近于的是( )A、 B、 C、 D、6. 《姑苏繁华图》是清代苏州籍宫廷画家徐扬的作品,全长 , 反映的是当时苏州“商贾辐辏,百货骈阗”的市井风情.如图,已知局部临摹画面装裱前是一个长为 , 宽为的矩形,装裱后的长与宽的比是 , 且四周边衬的宽度相等.设边衬的宽度为x(m),根据题意可列方程( ) A、 B、 C、 D、7. 如图,点P是▱ABCD边AD上的一点,E,F分别是BP,CP的中点,已知▱ABCD面积为16,那么△PEF的面积为( )
A、 B、 C、 D、7. 如图,点P是▱ABCD边AD上的一点,E,F分别是BP,CP的中点,已知▱ABCD面积为16,那么△PEF的面积为( ) A、8 B、6 C、4 D、28. 学校举行数学文化竞赛.图中的四个点分别描述了八(1)、八(2)、八(3)、八(4)四个班级竞赛成绩的优秀率y(班级优秀人数占班级参加竞赛人数的百分率)与该班参加竞赛人数x的情况,其中描述八(2)、八(4)两个班级情况的点恰好在同一个反比例函数的图象上,则成绩优秀人数最多的是( )
A、8 B、6 C、4 D、28. 学校举行数学文化竞赛.图中的四个点分别描述了八(1)、八(2)、八(3)、八(4)四个班级竞赛成绩的优秀率y(班级优秀人数占班级参加竞赛人数的百分率)与该班参加竞赛人数x的情况,其中描述八(2)、八(4)两个班级情况的点恰好在同一个反比例函数的图象上,则成绩优秀人数最多的是( )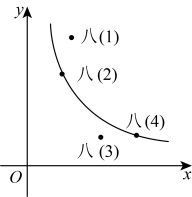 A、八(1)班 B、八(2)班 C、八(3)班 D、八(4)班
A、八(1)班 B、八(2)班 C、八(3)班 D、八(4)班二、填空题
-
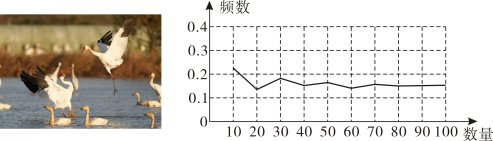
9. 分式有意义,则x满足的条件是 .10. 已知 , 则 .11. 计算: .12. 近年来,太湖区域环境保护效果显著,南迁的候鸟种群越来越多.为监测太湖某湿地过冬的国家二级重点保护野生动物灰鹤的数量,鸟类保护协会在该湿地中捕捉了30只灰鹤,戴上识别卡后放回,再利用鸟类智能识别追踪系统统计了飞回来的佩有识别卡的灰鹤频率,绘制了如图所示的折线统计图,由此估计该湿地约有灰鹤只.
 13. 某市为了解970万市民的出行情况,科学规划轨道交通,400名调查者走入1万户家庭发放了调查问卷,并对收回的3万份问卷进行了调查登记.该调查中的样本容量是 .14. 照相机成像应用了一个重要原理,用公式表示,其中f表示照相机镜头的焦距,u表示物体到镜头的距离,v表示胶片(像)到镜头的距离.若已知f、v , 则 .15. “方胜”是以两个菱形压角相叠而构成的几何图形或纹样,既寓意“双合同心”,又暗含“优胜、佳美”之意.如图是铜胎画珐琅山水图方胜盖盒,它由两个全等的正方形重叠而成,其中重叠部分也是正方形.已知该盖盒的长为(点A、B之间的距离),宽为(点C、D之间的距离),则重叠部分的正方形面积为 .
13. 某市为了解970万市民的出行情况,科学规划轨道交通,400名调查者走入1万户家庭发放了调查问卷,并对收回的3万份问卷进行了调查登记.该调查中的样本容量是 .14. 照相机成像应用了一个重要原理,用公式表示,其中f表示照相机镜头的焦距,u表示物体到镜头的距离,v表示胶片(像)到镜头的距离.若已知f、v , 则 .15. “方胜”是以两个菱形压角相叠而构成的几何图形或纹样,既寓意“双合同心”,又暗含“优胜、佳美”之意.如图是铜胎画珐琅山水图方胜盖盒,它由两个全等的正方形重叠而成,其中重叠部分也是正方形.已知该盖盒的长为(点A、B之间的距离),宽为(点C、D之间的距离),则重叠部分的正方形面积为 .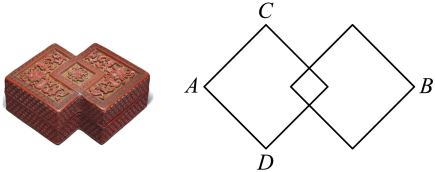 16. 如图,将四边形纸片沿折叠,使点落在上的点处,点在上;再将、分别沿、折叠,此时点、都落在上的点处.若 , 则当四边形是平行四边形时, .
16. 如图,将四边形纸片沿折叠,使点落在上的点处,点在上;再将、分别沿、折叠,此时点、都落在上的点处.若 , 则当四边形是平行四边形时, .
三、解答题
-
17. 计算: .18. 解方程: .19. 先化简,再求值: , 其中.20. 为了解某校落实中共中央国务院《关于全面加强新时代大中小学劳动教育的意见》的实施情况,有关部门从该校全体学生中随机抽取部分学生,调查他们平均每周劳动时间t(单位:h),以下是根据调查结果绘制的统计图表的一部分.
平均每周劳动时间频数统计表
时间t(h)
频数(人)
频率
10
0.2
35
a
0.05
合计
b
1
平均每周劳动时间频数分布直方图

(每组数据含最小值,不含最大值)
根据以上信息,回答下列问题:
(1)、 , ;(2)、若该校有1600名学生,请估计平均每周劳动时间在范围内的学生人数.21. 从2名男生和2名女生中,随机抽取2023年苏迪曼杯世界羽毛球混合团体锦标赛志愿者.(1)、抽取1名,恰好是女生的概率是;(2)、抽取2名,求恰好是1名男生和1名女生的概率.22. 如图,在中, . 将绕点A按逆时针方向旋转后得(其中),连接 . 当时,求的度数.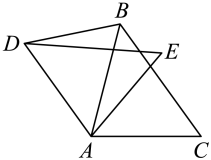 23. 2022年我国己成为全球最大的电动汽车市场,电动汽车在保障能源安全,改善空气质量等方面较传统汽车都有明显优势.经过对某款电动汽车和某款燃油车的对比调查发现,电动汽车平均每公里的充电费比燃油车平均每公里的加油费少元,且充电100元和加油400元时,两车行驶的总里程相同.
23. 2022年我国己成为全球最大的电动汽车市场,电动汽车在保障能源安全,改善空气质量等方面较传统汽车都有明显优势.经过对某款电动汽车和某款燃油车的对比调查发现,电动汽车平均每公里的充电费比燃油车平均每公里的加油费少元,且充电100元和加油400元时,两车行驶的总里程相同.请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
 24. 如图,一次函数与反比例函数的图像相交于点 , 与y轴相交于点B .
24. 如图,一次函数与反比例函数的图像相交于点 , 与y轴相交于点B .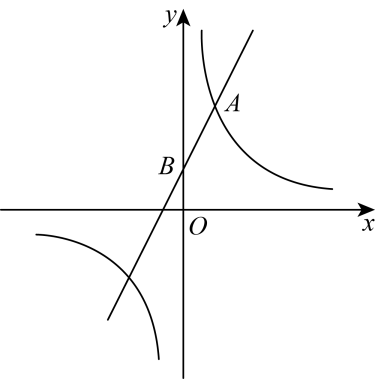 (1)、求k、b的值;(2)、点C是x轴上一点,若的面积为24,求点C的坐标.25. 如图,已知矩形 .
(1)、求k、b的值;(2)、点C是x轴上一点,若的面积为24,求点C的坐标.25. 如图,已知矩形 . (1)、用直尺和圆规分别在、边上找点E、F , 使得四边形是菱形;(保留作图痕迹,不写作法,并给出证明.)(2)、若 , , 求菱形的周长.26. 通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影.(1)、【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影长(不写画法);
(1)、用直尺和圆规分别在、边上找点E、F , 使得四边形是菱形;(保留作图痕迹,不写作法,并给出证明.)(2)、若 , , 求菱形的周长.26. 通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影.(1)、【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影长(不写画法);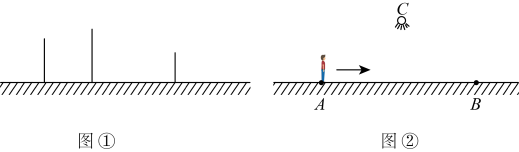 (2)、【数学思考】如图②,夜晚,小明从点A经过路灯C的正下方沿直线走到点B , 他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图像大致为____;A、
(2)、【数学思考】如图②,夜晚,小明从点A经过路灯C的正下方沿直线走到点B , 他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图像大致为____;A、 B、
B、 C、
C、 D、
D、 (3)、【解决问题】如图③,河对岸有一灯杆 , 在灯光下,小明在点D处测得自己的影长 , 沿方向前进到达点F处测得自己的影长 . 已知小明的身高为 , 求灯杆的高度.
(3)、【解决问题】如图③,河对岸有一灯杆 , 在灯光下,小明在点D处测得自己的影长 , 沿方向前进到达点F处测得自己的影长 . 已知小明的身高为 , 求灯杆的高度. 27. 如图,在中, , , . 动点P在射线上,将线段绕点C逆时针旋转得到线段 , 连接 .
27. 如图,在中, , , . 动点P在射线上,将线段绕点C逆时针旋转得到线段 , 连接 . (1)、面积的最小值为;(2)、当点P在的延长线上时,在图②中画出相应的图形,并证明:;(3)、当为等腰三角形时,求的长.
(1)、面积的最小值为;(2)、当点P在的延长线上时,在图②中画出相应的图形,并证明:;(3)、当为等腰三角形时,求的长.