黑龙江省哈尔滨市道里区2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-09-07 类型:期末考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 如图所示的图象分别给出了x与y的对应关系,其中表示y是x的函数的是( ).A、
 B、
B、 C、
C、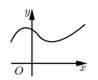 D、
D、 3. 由线段 , , 可以组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 若把直线向下平移个单位长度,得到图象对应的函数解析式是( )A、 B、 C、 D、5. 有一人患了流感,经过两轮传染后共有人患了流感,设每轮传染中平均一个人传染了人,则的值为( )A、 B、 C、 D、6. 已知一次函数的图象不经过第二象限,则的取值范围是( )A、 B、 C、 D、7. 如图,在菱形中,对角线与相交于点 , 过点作交的延长线于点 , 下列结论不一定正确的是( )
3. 由线段 , , 可以组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 若把直线向下平移个单位长度,得到图象对应的函数解析式是( )A、 B、 C、 D、5. 有一人患了流感,经过两轮传染后共有人患了流感,设每轮传染中平均一个人传染了人,则的值为( )A、 B、 C、 D、6. 已知一次函数的图象不经过第二象限,则的取值范围是( )A、 B、 C、 D、7. 如图,在菱形中,对角线与相交于点 , 过点作交的延长线于点 , 下列结论不一定正确的是( ) A、 B、 C、 D、是直角三角形8. 如图,菱形的对角线、相交于点 , 过点作于点 , 连接 , , 若菱形的面积为 , 则的长为( )
A、 B、 C、 D、是直角三角形8. 如图,菱形的对角线、相交于点 , 过点作于点 , 连接 , , 若菱形的面积为 , 则的长为( ) A、 B、 C、 D、9. 将矩形纸片按如图所示的方式折叠,、为折痕, , , 折叠后,点落在边上的处,并且点落在边上的处则的长为( )
A、 B、 C、 D、9. 将矩形纸片按如图所示的方式折叠,、为折痕, , , 折叠后,点落在边上的处,并且点落在边上的处则的长为( ) A、 B、 C、 D、10. 如图,在正方形中,对角线和相交于点 , 点在上,连接 , 过点作的垂线交于点 , 连接 , 过点作垂足为点 , 以为边作等边三角形 , 连接交于点 , 下列四个命题或结论:;;;若 , 则四边形的面积是其中正确的有( )
A、 B、 C、 D、10. 如图,在正方形中,对角线和相交于点 , 点在上,连接 , 过点作的垂线交于点 , 连接 , 过点作垂足为点 , 以为边作等边三角形 , 连接交于点 , 下列四个命题或结论:;;;若 , 则四边形的面积是其中正确的有( ) A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题(本大题共10小题,共30.0分)
-
11. 函数y= 中,自变量x的取值范围是.12. 已知是方程的一个根,则的值是 .13. 若是关于的正比例函数,则常数的值是 .14. 已知 , 是方程的两个根,则 .15. 已知关于的一元二次方程有两个不相等的实数根,则实数的取值范围是 .16. 已知一次函数的图象如图所示,不等式的解集是 .
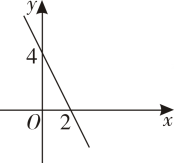 17. 如图所示,有一根高为米的电线杆在处断裂,电线杆顶部落在离电线杆底部点米远的地方,则电线杆断裂处离地面的距离的长为 .
17. 如图所示,有一根高为米的电线杆在处断裂,电线杆顶部落在离电线杆底部点米远的地方,则电线杆断裂处离地面的距离的长为 . 18. 我国古代数学家赵爽创制了一幅“赵爽弦图”,极富创新意识地给出了勾股定理的证明如图所示,“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形若大正方形的面积是 , 小正方形的面积是 , 则的长度是 .
18. 我国古代数学家赵爽创制了一幅“赵爽弦图”,极富创新意识地给出了勾股定理的证明如图所示,“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形若大正方形的面积是 , 小正方形的面积是 , 则的长度是 . 19. 已知:正方形 , 点是边上的点,连接 , 点是正方形边上的一点,连接 , 若 , 正方形边长为 , 则的长度是 .20. 如图,在矩形中,对角线上有两动点和 , 连接和 , 若 , , , 则的最小值是 .
19. 已知:正方形 , 点是边上的点,连接 , 点是正方形边上的一点,连接 , 若 , 正方形边长为 , 则的长度是 .20. 如图,在矩形中,对角线上有两动点和 , 连接和 , 若 , , , 则的最小值是 .
三、解答题(本大题共7小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
-
21. 解方程:(1)、;(2)、 .22. 如图,图、图是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为个单位,线段的两个端点均在小正方形的顶点上.
 (1)、在图1中画出一个以线段为对角线,面积为的矩形 , 且点和点均在小正方形的顶点上;(2)、在图2中画出一个以线段为一边,面积为的平行四边形 , 且点和点均在小正方形的顶点上画出一个即可 , 直接写出平行四边形的周长.23. 已知:、两地距离 , 甲、乙两人都从地出发前往地,乙比甲晚出发 , 甲、乙两人全程匀速运动,设运动时间为单位: , 甲、乙距离地的路程分别为 , 单位: , , 分别与的函数关系如图所示.
(1)、在图1中画出一个以线段为对角线,面积为的矩形 , 且点和点均在小正方形的顶点上;(2)、在图2中画出一个以线段为一边,面积为的平行四边形 , 且点和点均在小正方形的顶点上画出一个即可 , 直接写出平行四边形的周长.23. 已知:、两地距离 , 甲、乙两人都从地出发前往地,乙比甲晚出发 , 甲、乙两人全程匀速运动,设运动时间为单位: , 甲、乙距离地的路程分别为 , 单位: , , 分别与的函数关系如图所示. (1)、分别求 , 关于的函数解析式;(2)、在两人共同行走的过程中,求运动时间为多少时,两人相距 .24. 如图,在四边形中,和相交于点 , , .
(1)、分别求 , 关于的函数解析式;(2)、在两人共同行走的过程中,求运动时间为多少时,两人相距 .24. 如图,在四边形中,和相交于点 , , . (1)、如图1,求证:四边形是平行四边形;(2)、如图2, , , 分别是 , , 的中点,连接、、、 , 和相交于点 , 当和满足什么样的数量关系时才能使四边形为菱形,并说明你的理由.25. 某绘画艺人第一天的收入为元,第三天的收入为元每天收入的增长率相同 .
(1)、如图1,求证:四边形是平行四边形;(2)、如图2, , , 分别是 , , 的中点,连接、、、 , 和相交于点 , 当和满足什么样的数量关系时才能使四边形为菱形,并说明你的理由.25. 某绘画艺人第一天的收入为元,第三天的收入为元每天收入的增长率相同 . (1)、求绘画艺人每天平均收入的增长率是多少?(2)、绘画艺人想制作一幅长分米,宽分米的一幅画,其中有一横一竖宽度相同的彩条阴影部分为彩条无费用 , 其余空白处进行作画,如图所示,作画区域的费用为每平方分米元,经预算作画区域的总费用恰好是第四天的收入,求彩条的宽度是多少分米.26. 如图是一个三角点阵,从上向下数有无数多行,其中第一行有个点,第二行有个点第行有个点 .
(1)、求绘画艺人每天平均收入的增长率是多少?(2)、绘画艺人想制作一幅长分米,宽分米的一幅画,其中有一横一竖宽度相同的彩条阴影部分为彩条无费用 , 其余空白处进行作画,如图所示,作画区域的费用为每平方分米元,经预算作画区域的总费用恰好是第四天的收入,求彩条的宽度是多少分米.26. 如图是一个三角点阵,从上向下数有无数多行,其中第一行有个点,第二行有个点第行有个点 . (1)、根据上面的内容,请直接写出是三角点阵中前行的点数和;(2)、请直接写出三角点阵中前行的点数和;(3)、三角点阵中前行的点数和能是吗?如果能,请求出 , 如果不能,请说明理由;(4)、如果把图的三角点阵中各行的点数依次换为 , , , , , , 你能探究出前行的点数和满足什么规律吗?这个三角点阵中前行的点数和能是吗?如果能,请求出 , 如
(1)、根据上面的内容,请直接写出是三角点阵中前行的点数和;(2)、请直接写出三角点阵中前行的点数和;(3)、三角点阵中前行的点数和能是吗?如果能,请求出 , 如果不能,请说明理由;(4)、如果把图的三角点阵中各行的点数依次换为 , , , , , , 你能探究出前行的点数和满足什么规律吗?这个三角点阵中前行的点数和能是吗?如果能,请求出 , 如果不能,请说明理由.
27. 已知:在平面直角坐标系中,直线分别交轴和轴于点和点 , 且 . (1)、如图 , 求直线的解析式;(2)、如图 , 把沿翻折得到点和点是对应点 , 点在的延长线上,连接 , 过点作 , 垂足为点 , 交于点 , 连接 , 求的度数;(3)、如图 , 在(2)的条件下,过点作的平行线,分别交和轴于点和点 , 连接 , 的面积是 , 且 , 求点的坐标.
(1)、如图 , 求直线的解析式;(2)、如图 , 把沿翻折得到点和点是对应点 , 点在的延长线上,连接 , 过点作 , 垂足为点 , 交于点 , 连接 , 求的度数;(3)、如图 , 在(2)的条件下,过点作的平行线,分别交和轴于点和点 , 连接 , 的面积是 , 且 , 求点的坐标.