黑龙江省大庆市杜尔伯特县2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-09-07 类型:期末考试
一、选择题(每题3分,共30分每小题给出的四个选项中只有一个选项符合要求)
-
1. 2的算术平方根是( )A、 B、 C、 D、42. 在平面直角坐标系中,一次函数 的图象是( )A、
 B、
B、 C、
C、 D、
D、 3. 我国是最早了解勾股定理的国家之一,下面四幅图中,不能证明勾股定理的是( )A、
3. 我国是最早了解勾股定理的国家之一,下面四幅图中,不能证明勾股定理的是( )A、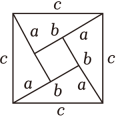 B、
B、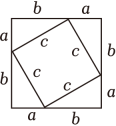 C、
C、 D、
D、 4. 在函数 中,自变量 的取值范围是( )A、 B、 C、 D、 且5. 如图,把一张长方形纸片 沿 折叠, ,则 ( )
4. 在函数 中,自变量 的取值范围是( )A、 B、 C、 D、 且5. 如图,把一张长方形纸片 沿 折叠, ,则 ( )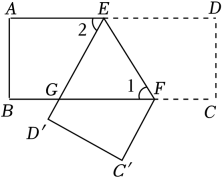 A、 B、 C、 D、6. 如图,是一个棱长为1的正方体纸盒.若一只蚂蚁要沿着正方体纸盒的表面,从顶点 爬到顶点 去觅食,则需要爬行的最短路程是( )
A、 B、 C、 D、6. 如图,是一个棱长为1的正方体纸盒.若一只蚂蚁要沿着正方体纸盒的表面,从顶点 爬到顶点 去觅食,则需要爬行的最短路程是( ) A、 B、2 C、 D、37. 直角三角形的两条直角边的长分别为5和12,则斜边上的高为( )A、 B、 C、6 D、138. 一组数据13、11、16、8、9、9、17的中位数和众数是( )A、11,9 B、8,9 C、9,9 D、8,139. 已知点 ,点 ,且 轴,则 的值为( )A、 B、2 C、 D、310. 已知直线 与 的交点为 ,则方程组 的解为( )A、 B、 C、 D、
A、 B、2 C、 D、37. 直角三角形的两条直角边的长分别为5和12,则斜边上的高为( )A、 B、 C、6 D、138. 一组数据13、11、16、8、9、9、17的中位数和众数是( )A、11,9 B、8,9 C、9,9 D、8,139. 已知点 ,点 ,且 轴,则 的值为( )A、 B、2 C、 D、310. 已知直线 与 的交点为 ,则方程组 的解为( )A、 B、 C、 D、二、填空题(每小题共3分,共24分)
-
11. 计算: .12. 已知 ,则 的平方根是 .13. 如图,在边长为1的正方形网格中, , , 均在格点上,则阴影部分的周长为 .
 14. 如图,正方形边长为1, ,则数轴上点 对应的数是 .
14. 如图,正方形边长为1, ,则数轴上点 对应的数是 . 15. 已知1,2,3,4, , , 的平均数是5,那么 的值是 .16. 点 , , , 在一次函数 的图象上,当 时,则 (填 , 或 .17. 若方程 的一个解是 ,则 .18. 在平面直角坐标系中,若点 与点 之间的距离是2,则 的值是 .
15. 已知1,2,3,4, , , 的平均数是5,那么 的值是 .16. 点 , , , 在一次函数 的图象上,当 时,则 (填 , 或 .17. 若方程 的一个解是 ,则 .18. 在平面直角坐标系中,若点 与点 之间的距离是2,则 的值是 .三、解答题(本大题共10小题,共66分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
-
19. 计算:(1)、 ;(2)、 .20. 解方程组: .21. 如图, ,点 是 延长线上一点, ,求证: .
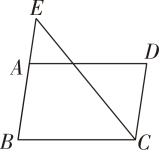 22. 如图,这是某校的平面示意图,如以正东为x轴正方向,正北为y轴正方向建立平面直角坐标系后,得到初中楼的坐标是 , 实验楼的坐标是 .
22. 如图,这是某校的平面示意图,如以正东为x轴正方向,正北为y轴正方向建立平面直角坐标系后,得到初中楼的坐标是 , 实验楼的坐标是 . (1)、坐标原点应为的位置.(2)、在图中画出此平面直角坐标系;(3)、校门在第象限;图书馆的坐标是;分布在第一象限的是 .23. 某中学七年级(1)班去体育用品商店买一些篮球和排球,供班上同学进行体育锻炼时使用,共买了2个篮球和6个排球,花570元,并且每个排球比篮球便宜25元.(1)、求篮球和排球的单价各是多少;(2)、商店里搞活动,有两种套餐,①套餐打折:五个篮球和五个排球为一套餐,套餐打八折;②满减活动:满999减100,满1999减200;两种活动不重复参与,学校打算购买14个篮球,12个排球,请问如何安排更划算?24. 如图,在平面直角坐标系中, , , .
(1)、坐标原点应为的位置.(2)、在图中画出此平面直角坐标系;(3)、校门在第象限;图书馆的坐标是;分布在第一象限的是 .23. 某中学七年级(1)班去体育用品商店买一些篮球和排球,供班上同学进行体育锻炼时使用,共买了2个篮球和6个排球,花570元,并且每个排球比篮球便宜25元.(1)、求篮球和排球的单价各是多少;(2)、商店里搞活动,有两种套餐,①套餐打折:五个篮球和五个排球为一套餐,套餐打八折;②满减活动:满999减100,满1999减200;两种活动不重复参与,学校打算购买14个篮球,12个排球,请问如何安排更划算?24. 如图,在平面直角坐标系中, , , .
⑴在图中作出 关于 轴的对称图形△ ;
⑵写出点 , , 的坐标;
⑶在 轴上找出点 ,使得 的值最小,并写出最小值.
25. 某校为丰富同学们的课余生活,全面提高科学素养,提升思维能力和科技能力,开展了“最强大脑”邀请赛,现从七、八年级中各随机抽取了20名学生的初赛成绩(初赛成绩均为整数,满分为10分,9分及以上为优秀)统计、整理如下:七年级抽取的学生的初赛成绩:6,6,7,7,7,8,8,8,8,8,9,9,9,9,9,9,9,10,10,10.
七、八年级抽取的学生的初赛成绩统计表:
年级
平均数
中位数
众数
方差
优秀率
七年级
8.5
a
八年级
8
7

根据以上信息,解答下列问题:
(1)、填空: , ;(2)、若该校八年级有900名学生参加初赛,规定满分才可进入复赛,估计八年级进入复赛的学生人数为多少人.(3)、根据以上数据,你认为七、八年级学生在“最强大脑”邀请赛中,哪个年级的学生初赛成绩更好?请说明理由;(写出一条理由即可)26. 如图1,已知圆柱形水槽的高为 ,在圆柱形水槽中放入一个正方体铁块,现以一定的速度往水槽中注水,图2是圆柱形水槽内水面高度 随时间 (分钟)变化的函数关系图象,观察图中所提供的信息,解答下列问题: (1)、水槽内正方体铁块的边长为 ;(2)、求 所在直线的函数关系式;(3)、该水槽恰好注满水需要多少分钟?27. 要度量作业纸上两条相交直线 、 所夹锐角 的大小,发现其交点不在作业纸内,无法直接度量.
(1)、水槽内正方体铁块的边长为 ;(2)、求 所在直线的函数关系式;(3)、该水槽恰好注满水需要多少分钟?27. 要度量作业纸上两条相交直线 、 所夹锐角 的大小,发现其交点不在作业纸内,无法直接度量.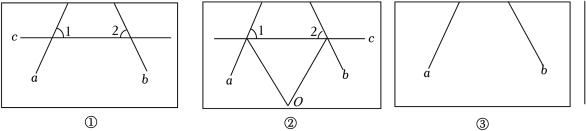 (1)、小明的方案:画直线 与 、 相交,如图①,测得 , ,则 (用含 、 的代数式表示);(2)、小刚的方案:画直线 与 、 相交,再画 、 相邻的外角的角平分线交于点 ,如图②,则得 ,则 (用含 的代数式表示);(3)、你还有什么方法,请在图③中补全,写出必要的文字说明.28. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,是它们离甲地距离 (千米)与时间 (小时)之间的函数关系图象,请根据图象解答下列问题:
(1)、小明的方案:画直线 与 、 相交,如图①,测得 , ,则 (用含 、 的代数式表示);(2)、小刚的方案:画直线 与 、 相交,再画 、 相邻的外角的角平分线交于点 ,如图②,则得 ,则 (用含 的代数式表示);(3)、你还有什么方法,请在图③中补全,写出必要的文字说明.28. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,是它们离甲地距离 (千米)与时间 (小时)之间的函数关系图象,请根据图象解答下列问题: (1)、线段 表示轿车在途中停留了小时;(2)、求线段 和线段 的解析式;(3)、当货车与轿车和甲地等距离时,轿车在行驶过程中所用的时间是多少?
(1)、线段 表示轿车在途中停留了小时;(2)、求线段 和线段 的解析式;(3)、当货车与轿车和甲地等距离时,轿车在行驶过程中所用的时间是多少?