黑龙江省哈尔滨市香坊区2022-2023学年七年级下册数学期末试卷

试卷更新日期：2023-09-07 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列方程中是二元一次方程的是（）

A、 $3 x + 2 = - 7$ B、 $x + 3 = 5 y$ C、 $\frac{1}{x} - y$ D、 $\frac{2}{3} x y = 1$

查看试题解析
2. 要组成一个三角形，三条线段长度可取（）.

A、9，6，13 B、15，6，8 C、2，3，5 D、3，5，9

查看试题解析
3. 不等式 $2 x + 5 > 1$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，生活中都把自行车的几根梁做成三角形的支架，这是利用三角形的（）

A、全等形 B、稳定性 C、灵活性 D、对称性

查看试题解析
5. 如图，亮亮书上三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）

A、 $S S S$ B、 $S A S$ C、 $A S A$ D、 $A A S$

查看试题解析
6. 关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} m x + y = n \\ x - n y = 2 m \end{array}$ 的解是 ${\begin{array}{l} x = 0 \\ y = 2 \end{array}$ ，则 $m + n$ 的值为（）

A、0 B、1 C、2 D、4

查看试题解析
7. 一个多边形的内角和等于外角和的两倍，那么这个多边形是（）

A、三边形 B、四边形 C、五边形 D、六边形

查看试题解析
8. 若关于 $x$ 的不等式 ${\begin{array}{l} x > 4 \\ x > m \end{array}$ 的解集为 $x > 4$ ，则 $m$ 的取值范围是（）

A、 $m > 4$ B、 $m < 4$ C、 $m \geq 4$ D、 $m \leq 4$

查看试题解析
9. 小明在文化用品超市购买单价为2元的签字笔和单价为3元的笔记本，一共花了17元，则购买方案有（）种.

A、1 B、2 C、3 D、4

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $A C = 2 A B$ ， $A D$ 是角平分线， $B F ⊥ A D$ 于点 $F$ ，交 $A C$ 于点 $E$ ，过点 $C$ 作 $C G ⊥ B F$ 于点 $G$ ，下列结论：① $B F = E F$ ；② $A F = C G$ ；③ $A D = C D$ ；④ $∠ A E B = ∠ A D B$ .其中正确的有（）个.

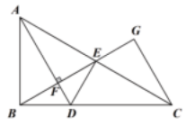A、1 B、2 C、3 D、4

查看试题解析

二、填空题（每题3分，共30分）

11. 把二元一次方程 $2 x - y = 6$ 化成用含x的式子表示y的形式，则 $y =$ ．

查看试题解析
12. 若 $a < b$ ，那么 $- 3 a$ $- 3 b$ （填“>”“<”或“=”）.

查看试题解析
13. 已知一组数据1， $m$ ， 3，9的平均数是4，则 $m$ 的值为.

查看试题解析
14. 若点 $P (m + 1 ， 3 - m)$ 在第二象限，则 $m$ 的取值范围是.

查看试题解析
15. 在 $△ A B C$ 中， $∠ A + ∠ B = 100 °$ ， $∠ C = 2 ∠ A$ ，则 $∠ B$ 的度数为.

查看试题解析
16. 定义运算“☆”，规定 $x ☆ y = a x + b y$ ，其中 $a$ 、 $b$ 为常数，若 $1 ☆ 2 = 5$ ， $2 ☆ 1 = 6$ ，则 $3 ☆ 3 =$ .

查看试题解析
17. 如图，小明与小红玩跷跷板游戏，如果跷跷板的支点 $O$ （即跷跷板 $F G$ 的中点）至地面的距离是50cm，当小红从水平位置 $C D$ 下降30cm时，这时小明离地面的高度是cm.

查看试题解析
18. 思政课上举行了普法知识竞赛，共有30道题，规定答对一题得4分，答错或者不答扣1分，在这次竞赛中张明明要不低于90分，则他至少需要答对道题.

查看试题解析
19. 已知 $A D$ 、 $A E$ 分别是 $△ A B C$ 高线和角平分线， $∠ B = 30 °$ ， $∠ A C D = 50 °$ ，则 $∠ E A D$ 的度数为°.

查看试题解析
20. 如图，在 $△ A B C$ 中， $B D$ 平分 $∠ A B C$ ， $A D ⊥ B D$ ，若 $A B ： B C = 5 ： 7$ ， $S_{△ A D C} = 8$ ，则 $S_{△ A B D} =$ .

查看试题解析

三、解答题（第21、22题，每题7分，第23、24题，每题8分，第25至27题，每题10分，共60分）

21.

(1)、解方程组： ${\begin{array}{l} x - y = 3 \\ 3 x - 8 y = 14 \end{array}$ ；

(2)、解不等式 $\frac{2 + x}{2} \geq \frac{2 x - 1}{3}$ ，并在数轴上表示解集.

查看试题解析
22. 如图，方格纸中，每个小正方形的边长均为1，点 $A$ ，点 $B$ ，点 $C$ 在小正方形的顶点上。
⑴画出 $△ A B C$ 中边 $B C$ 上的高 $A D$ ；
⑵画出 $△ A B C$ 中边 $A C$ 上的中线 $B E$ ；
⑶直接写出 $△ A B E$ 的面积为 .

查看试题解析
23. 香坊区某学校开展读书活动，为了解学生的参与程度，从全校学生中随机抽取200人进行问卷调查，获取了他们每人平均每天的阅读时间m（单位：分钟）将收集的数据分为A ， B ， C ， D ， E五个等级，绘制成如下的统计表及如图所示的统计图（不完整）：
平均每天阅读时间统计表
等级
人数（频数）
A（ $10 \leq m < 20$ ）
5
B（ $20 \leq m < 30$ ）
10
C（ $30 \leq m < 40$ ）
$x$
D（ $40 \leq m < 50$ ）
80
E（ $50 \leq m < 60$ ）
$y$
请根据图表中的信息，解答下列问题：

(1)、求 $x$ 的值.

(2)、这组数据的中位数所在的等级是.

(3)、学校拟将平均每天阅读时间不低于50分钟的学生评为“阅读达人”，并予以表扬若全校学生以1800人计算，估计受表扬的学生有多少人.

查看试题解析
24. 如图1，已知 $R t △ A B C ≌ R t △ A D E$ ， $∠ A B C = ∠ A D E = 90 °$ ， $B C$ 与 $D E$ 交于点 $F$ .

(1)、求 $∠ A C B + ∠ D A E$ 的度数；

(2)、如图2，连接 $A F$ ，在不添加辅助线的情况下，请直接写出图中所有全等三角形（不包括已知全等三角形）

查看试题解析
25. 香坊区某校开展大课间活动，某班需要购买A ， B两种跳绳，已知购买10根A种跳绳和5根B种跳绳共需175元；购买15根A种跳绳和10根B种跳绳共需300元.

(1)、购买1根A种跳绳和1根B种跳绳各需多少元？

(2)、若班级计划购买A ， B两种跳绳共45根，所花费用不多于550元，那么该班最少购买A种跳绳多少根？

查看试题解析
26. 在平面直角坐标系中，点O为坐标原点，点A的坐标为 $(0 ， a)$ ， B的坐标为 $(b ， 0)$ ，实数a、b满足 ${\begin{array}{l} a + b = 14 \\ 2 a - b = 4 \end{array}$ ，连接 $A B$ ， $A B = 10$ .

(1)、求a和b的值；

(2)、如图1，动点P以每秒2个单位长度的速度从点A出发沿着线段 $A B$ 方向向终点B运动，连接 $O P$ ，若 $△ B O P$ 的面积为 $S (S \neq 0)$ ，运动时间为 $t$ 秒，求 $S$ 与 $t$ 之间的关系式；

(3)、如图2，在（2）的条件下，过B作x轴垂线交 $O P$ 延长线于点C ，点D在 $O C$ 上，若 $2 ∠ B A O + ∠ D A B = 180 °$ ， $∠ A D O = ∠ O C B$ ，求此时的P点坐标.

查看试题解析
27. 在 $△ A B C$ 中， $∠ B A C = 60 °$ ，线段 $B F$ 、 $C E$ 分别平分 $∠ A B C$ 、 $∠ A C B$ 交于点G.

(1)、如图1，求 $∠ B G C$ 的度数；

(2)、如图2，求证： $E G = F G$ ；

(3)、如图3，过点C作 $C D ⊥ E C$ 交 $B F$ 延长线于点D ，连接 $A D$ ，点N在 $B A$ 延长线上，连接 $N G$ 交 $A C$ 于点 $M$ ，使 $∠ D A C = ∠ N G D$ ，若 $E B ： F C = 1 ： 2$ ， $C G = 10$ ，求线段 $M N$ 的长，

查看试题解析

等级	人数（频数）
A（ $10 \leq m < 20$ ）	5
B（ $20 \leq m < 30$ ）	10
C（ $30 \leq m < 40$ ）	$x$
D（ $40 \leq m < 50$ ）	80
E（ $50 \leq m < 60$ ）	$y$