黑龙江省哈尔滨市巴彦县2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-09-07 类型:期末考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
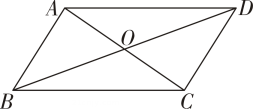
1. 以下哪一个方差对应的数据最稳定( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列图形中对称轴条数最多的图形是( )A、等边三角形 B、矩形 C、菱形 D、正方形4. 如图,在平行四边形中, , 与相交于点 , 若 , , 则的长为( )
 A、 B、 C、 D、5. 下列各组数中是勾股数的是( )A、 , , B、 , , C、 , , D、 , ,6. 一次函数经过第一、二、三象限,则下列正确的是( )A、 , B、 , C、 , D、 ,7. 已知点 , 点是直线上的两点,则和的大小关系为( )A、 B、 C、 D、无法确定8. 一次函数y=2x-6的图象是由一次函数y=2x+3的图象得到的( )A、向上平移9个单位长度 B、向左平移9个单位长度 C、向右平移9个单位长度 D、向下平移9个单位长度9. 已知 , 点 , 分别为 , 上的点,连接 , , 若 , 则两直线与间的距离是( )A、 B、 C、 D、10. 小明上午:从家里出发,跑步去他家附近的抗口纪念馆参加抗美援朝周年纪念活动,然后从纪含馆原路返回家中,小明离家的路程米和经过的时间分之间的函数关系如图所示,下列说法不正确的是( )
A、 B、 C、 D、5. 下列各组数中是勾股数的是( )A、 , , B、 , , C、 , , D、 , ,6. 一次函数经过第一、二、三象限,则下列正确的是( )A、 , B、 , C、 , D、 ,7. 已知点 , 点是直线上的两点,则和的大小关系为( )A、 B、 C、 D、无法确定8. 一次函数y=2x-6的图象是由一次函数y=2x+3的图象得到的( )A、向上平移9个单位长度 B、向左平移9个单位长度 C、向右平移9个单位长度 D、向下平移9个单位长度9. 已知 , 点 , 分别为 , 上的点,连接 , , 若 , 则两直线与间的距离是( )A、 B、 C、 D、10. 小明上午:从家里出发,跑步去他家附近的抗口纪念馆参加抗美援朝周年纪念活动,然后从纪含馆原路返回家中,小明离家的路程米和经过的时间分之间的函数关系如图所示,下列说法不正确的是( )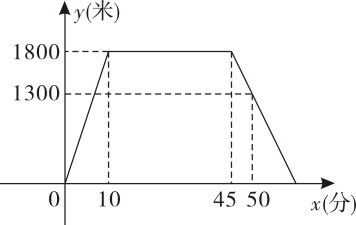 A、小明在纪念馆停留分钟 B、小明从家到纪念馆的平均速度为米分 C、小明从纪念馆返回家中的平均速度为米分 D、从小明家到纪念馆的路程是米
A、小明在纪念馆停留分钟 B、小明从家到纪念馆的平均速度为米分 C、小明从纪念馆返回家中的平均速度为米分 D、从小明家到纪念馆的路程是米二、填空题(本大题共10小题,共30.0分)
-
11. 数据 , , , , 的方差是 .12. 数据 , , , , , , 的众数是 .13. 函数y= 中自变量x的取值范围是 .
14. 计算:的结果为 .15. 平行四边形的周长为 , 一边长为 , 则另一条邻边长为 .16. 直线经过点 , 则的最大值等于 .17. 已知一次函数 , 当时,的最大值等于 .18. 如图,在平面直角坐标系中,菱形的顶点 , 的坐标分别为 , , , 则顶点的坐标为 .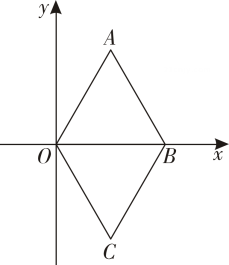 19. 已知,矩形 , 为的中点,为上一点,连接 , 若 , , , 则的长为 .20. 如图,在正方形中,点在上,且:: , 点为的中点,连接 , , 则 .
19. 已知,矩形 , 为的中点,为上一点,连接 , 若 , , , 则的长为 .20. 如图,在正方形中,点在上,且:: , 点为的中点,连接 , , 则 .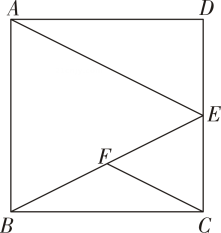
三、计算题(本大题共1小题,共7.0分)
-
21. 先化简,再求值: , 其中 .
四、解答题(本大题共6小题,共53.0分。解答应写出文字说明,证明过程或演算步骤)
-
22. 如图,方格线中每个小正方形的边长均为 , 线段 , 线段的端点均在小正方形的顶点上.
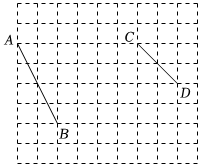
⑴在方格纸中画出以为直角顶点的 , 点在小正方形的顶点上,且的面积为;
⑵在方格纸中画出以为边的 , 点在小正方形的顶点上,且的面积为 , , 连接 , 直接写出线段的长.
23. 某校为丰富同学们的课余生活,全面提高科学素养,提升思维能力和科投能力,开展了“最强大脑”谢请赛,现从七、八年级中各随机抽取了20名学生的初赛成绩(初春成绩均为整数,满分为分)统计、根理如下:
七年级抽取学生的初赛成绩: , , , , , , , , , , , , , , , , , , , .七、八年级抽取的学生的初赛成绩统计表:
年级
七年级
八年级
平均数
中位数
众数
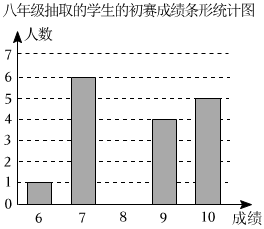 (1)、 , ;(2)、通过计算补全条形统计图;(3)、若该校八年级有名学生参加初赛,规定满分才可进入复赛,请估计八年级进入复赛?24. 已知矩形的对角线、相交于点 , 点是边上一点,连接、、 , 且 .
(1)、 , ;(2)、通过计算补全条形统计图;(3)、若该校八年级有名学生参加初赛,规定满分才可进入复赛,请估计八年级进入复赛?24. 已知矩形的对角线、相交于点 , 点是边上一点,连接、、 , 且 .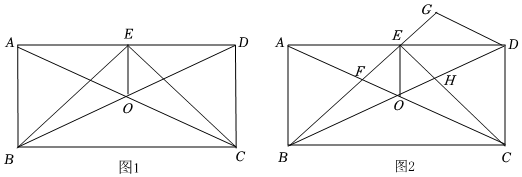 (1)、如图 , 求证:;(2)、如图 , 设与相交于点 , 与相交于点 , 过点作的平行线交的延长线于点 , 在不添加任何辅助线的情况下,请直接写出图中的四个三角形除外 , 使写出的每个三角形的面积都与的面积相等.25. 随着神舟十五号载人飞船顺利发射,人们对航天事业愈发关注,航天周边产品销量也逐渐提高某商场准备购进一批火箭模型进行售卖,已知一个款火箭模型比一个款火箭模型贵元,用元购入的款火箭模型与元购入的款火箭模型数量相同.(1)、这两款火箭模型的进货单价各是多少元?(2)、已知商场准备购进这两款火箭模型共个,后将这批火箭模型以款每个元,款每个元的价格出售求可获得的总利润元与其中款火箭模型的数量个之间的关系式.26. 在四边形中, , 对角线平分 , 点为边上一点,连接交于点 , .
(1)、如图 , 求证:;(2)、如图 , 设与相交于点 , 与相交于点 , 过点作的平行线交的延长线于点 , 在不添加任何辅助线的情况下,请直接写出图中的四个三角形除外 , 使写出的每个三角形的面积都与的面积相等.25. 随着神舟十五号载人飞船顺利发射,人们对航天事业愈发关注,航天周边产品销量也逐渐提高某商场准备购进一批火箭模型进行售卖,已知一个款火箭模型比一个款火箭模型贵元,用元购入的款火箭模型与元购入的款火箭模型数量相同.(1)、这两款火箭模型的进货单价各是多少元?(2)、已知商场准备购进这两款火箭模型共个,后将这批火箭模型以款每个元,款每个元的价格出售求可获得的总利润元与其中款火箭模型的数量个之间的关系式.26. 在四边形中, , 对角线平分 , 点为边上一点,连接交于点 , .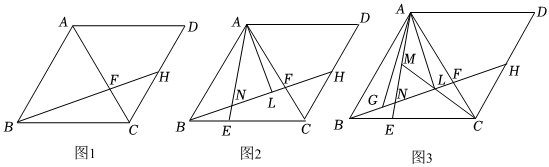 (1)、如图 , 求证:四边形是菱形;(2)、如图 , 点在上, , 交于点 , 于点 , 若 , 求证: .(3)、如图 , 在的条件下,为的中点,点在上,点在上,连接 , , , , 若 , 求线段的长,27. 如图 , 在平面直角坐标系中,点为坐标原点,直线与轴交于点 , 与轴交于点 , .
(1)、如图 , 求证:四边形是菱形;(2)、如图 , 点在上, , 交于点 , 于点 , 若 , 求证: .(3)、如图 , 在的条件下,为的中点,点在上,点在上,连接 , , , , 若 , 求线段的长,27. 如图 , 在平面直角坐标系中,点为坐标原点,直线与轴交于点 , 与轴交于点 , .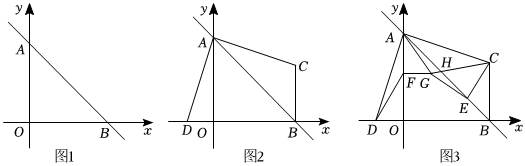 (1)、求直线的解析式;(2)、如图 , 点是轴负半轴上一点,连接 , 点在第一象限内, , 交于点 , 设点的横坐标为 , 线段的长为 , 求与之间的函数关系式不要求写出自变量的取值范围;(3)、如图 , 在的条件下, , 点在上,点在上, , , , 连接 , , , 交于点 , 若 , 求点的坐标.
(1)、求直线的解析式;(2)、如图 , 点是轴负半轴上一点,连接 , 点在第一象限内, , 交于点 , 设点的横坐标为 , 线段的长为 , 求与之间的函数关系式不要求写出自变量的取值范围;(3)、如图 , 在的条件下, , 点在上,点在上, , , , 连接 , , , 交于点 , 若 , 求点的坐标.
-