黑龙江省绥化市望奎县2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-09-07 类型:期末考试
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 如图,菱形ABCD中,对角线AC,BD相交于点O,若AB=5,AC=6,则BD的长是( )
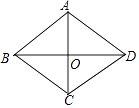 A、8 B、7 C、4 D、32. 下列式子中,为最简二次根式的是( )A、 B、 C、 D、3. 当时,函数的值等于( )A、 B、 C、 D、4. 在一次中小学田径运动会上,参加男子跳高的名运动员的成绩如表所示:这些运动员跳高成绩的众数是( )
A、8 B、7 C、4 D、32. 下列式子中,为最简二次根式的是( )A、 B、 C、 D、3. 当时,函数的值等于( )A、 B、 C、 D、4. 在一次中小学田径运动会上,参加男子跳高的名运动员的成绩如表所示:这些运动员跳高成绩的众数是( )成绩
人数
A、 B、 C、 D、5. 一次函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 已知一次函数y=kx+b,函数值y随自变量x的增大而减小,且kb>0,则函数y=kx+b的图象大致是( )A、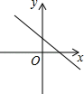 B、
B、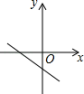 C、
C、 D、
D、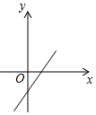 7. 学习全等三角形时,某班举行了以“生活中的全等”为主题的测试活动,全班学生的测试成绩统计如下表:
7. 学习全等三角形时,某班举行了以“生活中的全等”为主题的测试活动,全班学生的测试成绩统计如下表:得分(分)
85
89
93
96
100
人数(人)
4
6
15
13
2
则这些学生得分的中位数是( )
A、89 B、91 C、93 D、968. 如图,在平行四边形ABCD中,BC=10,AC=14,BD=8,则△BOC的周长是( )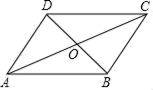 A、21 B、22 C、25 D、329. 正方形的边长为 , 在上,且 , 是上的一动点,的最小值为( )
A、21 B、22 C、25 D、329. 正方形的边长为 , 在上,且 , 是上的一动点,的最小值为( )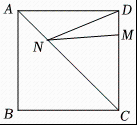 A、 B、 C、 D、10. 如图,以直角三角形的三边为边向外作正方形,根据图中数据,可得出正方形A的面积是( )
A、 B、 C、 D、10. 如图,以直角三角形的三边为边向外作正方形,根据图中数据,可得出正方形A的面积是( ) A、12 B、24 C、30 D、1011. 如图,边长为的等边和边长为的等边 , 它们的边 , 位于同一条直线上,开始时,点与点重合,固定不动,然后把自左向右沿直线平移,移出外点与点重合停止,设平移的距离为 , 两个三角形重合部分的面积为 , 则关于的函数图象是( )
A、12 B、24 C、30 D、1011. 如图,边长为的等边和边长为的等边 , 它们的边 , 位于同一条直线上,开始时,点与点重合,固定不动,然后把自左向右沿直线平移,移出外点与点重合停止,设平移的距离为 , 两个三角形重合部分的面积为 , 则关于的函数图象是( )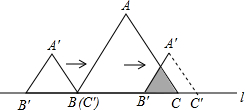 A、
A、 B、
B、 C、
C、 D、
D、 12. 如图,正方形中,点E、F、H分别是、、的中点,、交于G , 连接、 . 下列结论:①;②;③;④ , 其中正确的有( )
12. 如图,正方形中,点E、F、H分别是、、的中点,、交于G , 连接、 . 下列结论:①;②;③;④ , 其中正确的有( )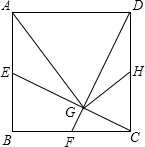 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共10小题,共30.0分)
-
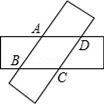
13. 已知直角三角形的两条直角边是3和5,则第三条边是14. 如图所示,将两张等宽的长方形条交叉叠放,重叠部分是一个四边形ABCD,若AD=4cm,∠ABC=30°,则四边形ABCD的面积是cm2 .
 15. .16. 代数式 中,实数m的取值范围是 .17. 已知三角形的面积是20,一边长为2 ,那么这条边上的高为 .18. 已知两边长为5和12,则其斜边上的中线为.19. 某校八年级甲、乙两班举行电脑汉字输入比赛,两个班参加比赛的学生每分钟输入汉字的个数经统计和计算后结果如下表:
15. .16. 代数式 中,实数m的取值范围是 .17. 已知三角形的面积是20,一边长为2 ,那么这条边上的高为 .18. 已知两边长为5和12,则其斜边上的中线为.19. 某校八年级甲、乙两班举行电脑汉字输入比赛,两个班参加比赛的学生每分钟输入汉字的个数经统计和计算后结果如下表:班级
参加人数
平均字数
中位数
方差
甲
乙
有一位同学根据上表得出如下结论:
①甲、乙两班学生的平均水平相同;
②乙班优秀的人数比甲班优秀的人数多每分钟输入汉字达个以上为优秀;
③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大.
上述结论正确的是填序号
20. 如图,在中,点D、E分别是边、的中点, , 则 .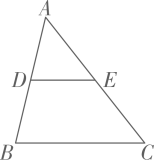 21. 若正比例函数的图象经过点A和点B , 且 , 而 , 则m的取值范围是 .22. 甲、乙两人在笔直的健身步道上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,则甲、乙两人距离的最大值是 米.
21. 若正比例函数的图象经过点A和点B , 且 , 而 , 则m的取值范围是 .22. 甲、乙两人在笔直的健身步道上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,则甲、乙两人距离的最大值是 米.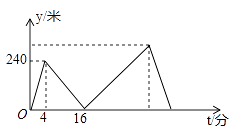
三、解答题(本大题共8小题,共54.0分。解答应写出文字说明,证明过程或演算步骤)
-
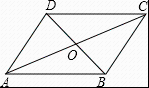
23. 计算: .24. 计算: .25. 如图,在四边形中,与相交于点 , , .
求证:四边形是平行四边形.
 26. 如图,在四边形中, , , , . 求的度数.
26. 如图,在四边形中, , , , . 求的度数.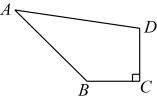 27. 如图,一次函数的图象与轴交于点B,与正比例函数的图象交于点 .
27. 如图,一次函数的图象与轴交于点B,与正比例函数的图象交于点 . (1)、求的面积;(2)、利用函数图象直接写出当时,x的取值范围.28. 一农民带了若干千克土豆进城出售,为了方便,他带了一些零用钱备用,按市场价出售一些土豆后,又降价出售,售出土豆的千克数与他手中持有的钱数(含备用钱)的关系如图.结合图象回答:
(1)、求的面积;(2)、利用函数图象直接写出当时,x的取值范围.28. 一农民带了若干千克土豆进城出售,为了方便,他带了一些零用钱备用,按市场价出售一些土豆后,又降价出售,售出土豆的千克数与他手中持有的钱数(含备用钱)的关系如图.结合图象回答: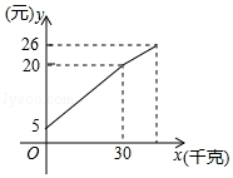 (1)、农民自带的零钱是元;(2)、降价前他每千克土豆出售的价格是元/千克;列出降价前售出土豆的千克数与他手中持有的钱数(含备用钱)的函数关系式为:;(3)、降价后他按每千克0.4元将土豆售完,这时他手中的钱(含备用钱)是26元,问他一共带了多少土豆去城里出售?29. 如图,是正方形对角线上一点, , 垂足分别是点、
(1)、农民自带的零钱是元;(2)、降价前他每千克土豆出售的价格是元/千克;列出降价前售出土豆的千克数与他手中持有的钱数(含备用钱)的函数关系式为:;(3)、降价后他按每千克0.4元将土豆售完,这时他手中的钱(含备用钱)是26元,问他一共带了多少土豆去城里出售?29. 如图,是正方形对角线上一点, , 垂足分别是点、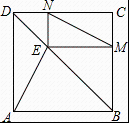 (1)、求证:;(2)、若 , , 求正方形的边长.30. 在“新冠病毒”防控期间,某医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进的同一商品进价相同,购进数量和所需费用如表所示:
(1)、求证:;(2)、若 , , 求正方形的边长.30. 在“新冠病毒”防控期间,某医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进的同一商品进价相同,购进数量和所需费用如表所示:项目
购进数量(件)
购进所需费用(元)
酒精消毒液
测温枪
第一次
30
40
8300
第二次
40
30
6400
(1)、求酒精消毒液和测温枪两种商品每件的进价分别是多少元?(2)、公司决定酒精消毒液以每件20元出售,测温枪以每件240元出售.为满足市场需求,需购进这两种商品共1000件.①若设购进测温枪m件,该公司销售完上述1000件商品获得的利润为W元,请写出W与m的函数关系式;
②若购买测温枪数量不超过200件,求该公司销售完上述1000件商品获得的最大利润.