黑龙江省哈尔滨市平房区教育联合体2022-2023学年七年级(下)期末数学试卷(五四学制)
试卷更新日期:2023-09-07 类型:期末考试
一、选择题(本大题共10小题,共30.0分。)
-
1. 的相反数是( )A、2 B、 C、 D、2. 如果“盈利”记作 , 那么表示( )A、少赚 B、亏损 C、盈利 D、亏损3. 下列计算正确的是( )A、 B、 C、 D、4. 下列调查中,调查方式选择合理的是( )A、为了了解某一品牌家具的甲醛含量,选择全面调查 B、为了了解某公园全年的游客流量,选择抽样调查 C、为了了解神舟飞船的设备零件的质量情况,选择抽样调查 D、为了了解一批袋装食品是否含有防腐剂,选择全面调查5. 下列说法中正确的是( )A、的系数是 B、的次数是 C、的次数是 D、的系数是6. 长方形的长是 , 宽是 , 则长方形的周长是( )A、 B、 C、 D、7.
如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
 A、传 B、统 C、文 D、化8. 曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光。如图, 两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( )
A、传 B、统 C、文 D、化8. 曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光。如图, 两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( ) A、两点之间,线段最短 B、平行于同一条直线的两条直线平行 C、垂线段最短 D、两点确定一条直线9. 有理数、在数轴上的位置如图所示,则数 , , , 的大小关系为( )
A、两点之间,线段最短 B、平行于同一条直线的两条直线平行 C、垂线段最短 D、两点确定一条直线9. 有理数、在数轴上的位置如图所示,则数 , , , 的大小关系为( ) A、 B、 C、 D、10. 下列说法:
A、 B、 C、 D、10. 下列说法:正数和负数统称为有理数;若 , 则、互为相反数;如果 , 则有;如果两个角的和等于 , 我们就说这两个角互余;有理数的倒数是 .
其中正确的有( )
A、个 B、个 C、个 D、个二、填空题(本大题共10小题,共30.0分)
-
11. 中国的陆地面积约为9 600 000km2 , 把9 600 000用科学记数法表示为 .12. 计算: .13. 若代数式 , 则代数式的值是 .14. 已知 , 则 .15. 如图,点是线段的中点,点是线段上一点, , 若线段 , 则 .
 16. 若单项式和是同类项,则的值为 .17. 一副三角板按如图所示的方式摆放,且的度数是∠2的3倍,则∠2的度数为 .
16. 若单项式和是同类项,则的值为 .17. 一副三角板按如图所示的方式摆放,且的度数是∠2的3倍,则∠2的度数为 . 18. 用棋子摆出下列一组三角形,三角形每边有n枚棋子,每个三角形的棋子总数为s,如图按此规律推断,当三角形的边上有n枚棋子时,该三角形棋子总数s=(用含n的式子表示).
18. 用棋子摆出下列一组三角形,三角形每边有n枚棋子,每个三角形的棋子总数为s,如图按此规律推断,当三角形的边上有n枚棋子时,该三角形棋子总数s=(用含n的式子表示).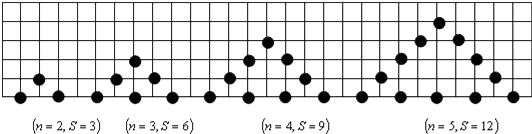 19. 数轴上点表示的数是 , 将点在数轴上平移个单位长度得到点 , 则平移后点表示的数是 .20. 如图,平分 , 平分若 , , 则 .
19. 数轴上点表示的数是 , 将点在数轴上平移个单位长度得到点 , 则平移后点表示的数是 .20. 如图,平分 , 平分若 , , 则 .
三、解答题(本大题共7小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
-
21. 计算(1)、;(2)、;(3)、;(4)、 .22. 如图,平面上有四个点 , , , , 根据下列语句画图:

⑴画直线 , 交于点;
⑵连接线段 , 交于点;
⑶连接线段 , 并将其反向延长.
23. 先化简,再求值: , 其中 , .24. 某地区为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,自来水公司将基本用水量定为每户吨,超出基本用水量的部分实行加价收费为更好地决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图每组数据包括右端点但不包括左端点 , 请你根据统计图解答下列问题: (1)、本次调查共抽取多少户的用水量数据?(2)、通过计算,补全频数分布直方图:(3)、该地区有万用户,请你通过样本估计总体中约有多少户的用水全部享受基本价格?25. 如图, , , 平分 , 平分 .
(1)、本次调查共抽取多少户的用水量数据?(2)、通过计算,补全频数分布直方图:(3)、该地区有万用户,请你通过样本估计总体中约有多少户的用水全部享受基本价格?25. 如图, , , 平分 , 平分 . (1)、如图1,求度数;(2)、如图2,若 , 其他条件不变,请直接写出的度数.26. 如图,一扇窗户,窗框为铝合金材料,上面是由三个大小相等的扇形组成的半圆窗框构成,下面是由两个大小相等的长 , 宽的长方形窗框构成,窗户全部安装玻璃本题中取 , 长度单位为米
(1)、如图1,求度数;(2)、如图2,若 , 其他条件不变,请直接写出的度数.26. 如图,一扇窗户,窗框为铝合金材料,上面是由三个大小相等的扇形组成的半圆窗框构成,下面是由两个大小相等的长 , 宽的长方形窗框构成,窗户全部安装玻璃本题中取 , 长度单位为米 (1)、一扇这样窗户一共需要铝合金多少米?用含 , 的式子表示(2)、一扇这样窗户一共需要玻璃多少平方米?铝合金窗框宽度忽略不计用含 , 的式子表示(3)、某公司需要购进扇这样的窗户,在同等质量的前提下,甲、乙两个厂商分别给出如表报价:
(1)、一扇这样窗户一共需要铝合金多少米?用含 , 的式子表示(2)、一扇这样窗户一共需要玻璃多少平方米?铝合金窗框宽度忽略不计用含 , 的式子表示(3)、某公司需要购进扇这样的窗户,在同等质量的前提下,甲、乙两个厂商分别给出如表报价:铝合金元米
玻璃元平方米
甲厂商
不超过平方米的部分,元平方米,超过平方米的部分,元平方米
乙厂商
元平方米,每购一平方米玻璃送米铝合金
当 , 时,该公司在哪家厂商购买窗户合算?
27. 如图所示,点表示数轴的原点,点在原点的左侧,所表示的数是 , 点在原点的右侧,所表示的数是 , 并且关于的多项式是三次二项式. (1)、求线段的长;(2)、动点从点出发,沿线段运动,到达点停止,速度是个单位长度秒,点为线段的中点,设运动时间为秒,请用含有的式子表示线段的长;(3)、在(2)的条件下,是否存在值,使线段的长度是?并说明理由.
(1)、求线段的长;(2)、动点从点出发,沿线段运动,到达点停止,速度是个单位长度秒,点为线段的中点,设运动时间为秒,请用含有的式子表示线段的长;(3)、在(2)的条件下,是否存在值,使线段的长度是?并说明理由.