黑龙江省大庆市杜尔伯特蒙古族自治县2022-2023学年八年级下学期7月期末数学试题
试卷更新日期:2023-09-07 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 关于x的一元二次方程的二次项系数、一次项系数、常数项分别是( )A、1, , B、 , , C、1, , 1 D、1,5,12. 若方程有两个不相等的实数根,则m的值可以是( )A、5 B、4 C、3 D、23. 如图是一把做工精湛的紫砂壶“景舟石瓢”,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 两个相似三角形的周长比是.则其相似比是( )A、 B、 C、 D、5. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、正六边形 B、平行四边形 C、正三角形 D、等腰梯形6. 如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为( )
4. 两个相似三角形的周长比是.则其相似比是( )A、 B、 C、 D、5. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、正六边形 B、平行四边形 C、正三角形 D、等腰梯形6. 如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为( )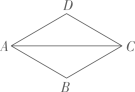 A、 B、1 C、 D、7. 如图,已知 , , , 那么的长为( )
A、 B、1 C、 D、7. 如图,已知 , , , 那么的长为( )
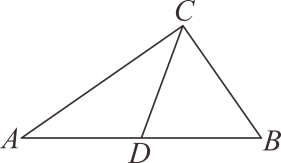
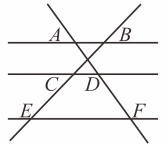 A、9 B、12 C、15 D、188. 如图,在中,D是边上的点, , , 则与的面积比是( )
A、9 B、12 C、15 D、188. 如图,在中,D是边上的点, , , 则与的面积比是( ) A、 B、1:2 C、1:3 D、1:49. 一个口袋中有红球、黄球共20个,这些除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一球,记下颜色后再放回口袋,不断重复这一过程,共摸了200次,发现其中有161次摸到红球.则这个口袋中红球数大约有( )A、4个 B、10个 C、16个 D、20个10. 已知点均在反比例函数的图象上,则 , 的大小关系是( )A、 B、 C、 D、
A、 B、1:2 C、1:3 D、1:49. 一个口袋中有红球、黄球共20个,这些除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一球,记下颜色后再放回口袋,不断重复这一过程,共摸了200次,发现其中有161次摸到红球.则这个口袋中红球数大约有( )A、4个 B、10个 C、16个 D、20个10. 已知点均在反比例函数的图象上,则 , 的大小关系是( )A、 B、 C、 D、二、填空题(每题3分,共24分)
-
11. 一元二次方程的解是 .12. 反比例函数的图象经过点 , 那么图像分布在象限.13. 若一元二次方程 , 则的值是 .14. 若 , 则 .15. 现有6张质地均匀,完全相同的纸片,分别写有“人”“民”“就”“是”“江”“山”6个汉字,现从中一次取出2张,刚好组成“人民”的概率为 .16. 如图,在中,是斜边上的中线,若 , 则 .
 17. 反比例函数在第一象限内的图象如图,点M是图象上一点垂直x轴于点P,如果的面积为2,那么k的值是 .
17. 反比例函数在第一象限内的图象如图,点M是图象上一点垂直x轴于点P,如果的面积为2,那么k的值是 .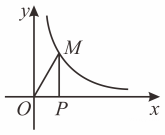 18. 如图,已知和是以点C为位似中心的位似图形,点的对应点为 , 点C位于处,若点B的对应点的横坐标为3,则点B的横坐标为 .
18. 如图,已知和是以点C为位似中心的位似图形,点的对应点为 , 点C位于处,若点B的对应点的横坐标为3,则点B的横坐标为 .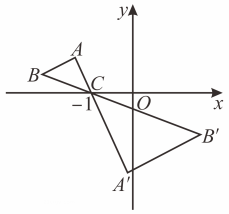
三、解答题(本大题10小题、共66分)
-
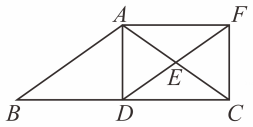
19. 解方程(1)、;(2)、 .20. 如图,在中, , 点D、E分别为、中点,连接并延长至点F,使得 , 连接、、 , 求证:四边形为矩形.
 21. 为推进党的“二十大精神”第一时间进课堂、进头脑,引导广大青少年坚定理想信念,把人生理想融入国家和民族发展的伟大“中国梦”之中,杜尔伯特县教育局开展了“二十大”主题教育演讲比赛,某学校从甲、乙2名男生和丙、丁、戊3名女生中随机选派一男一女进行宣讲.(1)、请利用画树状图或列表法,列举出所有可能选派的结果;(2)、求选派丁去演讲的概率.22. 如图,在平行四边形中,对角线与相交于点 , 于点 , 连接 . , , .
21. 为推进党的“二十大精神”第一时间进课堂、进头脑,引导广大青少年坚定理想信念,把人生理想融入国家和民族发展的伟大“中国梦”之中,杜尔伯特县教育局开展了“二十大”主题教育演讲比赛,某学校从甲、乙2名男生和丙、丁、戊3名女生中随机选派一男一女进行宣讲.(1)、请利用画树状图或列表法,列举出所有可能选派的结果;(2)、求选派丁去演讲的概率.22. 如图,在平行四边形中,对角线与相交于点 , 于点 , 连接 . , , . (1)、求证:四边形是菱形.(2)、求的周长23. 已知关于x的一元二次方程 .(1)、求证:无论m为何实数,方程总有两个实数根;(2)、若方程的两个实数根、满足 , 求m的值.24. 随着新能源汽车配套设施的不断普及,新能源汽车的销售量逐年增加,某小区物业统计2022年春节小区内停放新能源汽车数量正好是2020年春节小区内停放新能源汽车数量的1.96倍.(1)、求这两年小区内停放新能源汽车数量的平均增长率;(2)、若2022年春节小区内停放新能源汽车数量为490辆,且增长率保持不变,请估计到2023年春节该小区停放新能源汽车的数量.25. 某学校的自动饮水机,开机加热时水温每分钟上升 , 水温到时停止加热.此后水温开始下降.水温与开机通电时间成反比例关系.若水温在时接通电源.一段时间内,水温y与通电时间x之间的函数关系如图所示.
(1)、求证:四边形是菱形.(2)、求的周长23. 已知关于x的一元二次方程 .(1)、求证:无论m为何实数,方程总有两个实数根;(2)、若方程的两个实数根、满足 , 求m的值.24. 随着新能源汽车配套设施的不断普及,新能源汽车的销售量逐年增加,某小区物业统计2022年春节小区内停放新能源汽车数量正好是2020年春节小区内停放新能源汽车数量的1.96倍.(1)、求这两年小区内停放新能源汽车数量的平均增长率;(2)、若2022年春节小区内停放新能源汽车数量为490辆,且增长率保持不变,请估计到2023年春节该小区停放新能源汽车的数量.25. 某学校的自动饮水机,开机加热时水温每分钟上升 , 水温到时停止加热.此后水温开始下降.水温与开机通电时间成反比例关系.若水温在时接通电源.一段时间内,水温y与通电时间x之间的函数关系如图所示.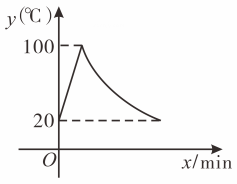 (1)、水温从加热到 , 需要;(2)、求水温下降过程中,y与x的函数关系式,并写出自变量取值范围;(3)、如果上午8点接通电源,那么8:20之前,不低于的时间有多少?26. 如图是由一些大小相同的小立方块搭成的几何体.
(1)、水温从加热到 , 需要;(2)、求水温下降过程中,y与x的函数关系式,并写出自变量取值范围;(3)、如果上午8点接通电源,那么8:20之前,不低于的时间有多少?26. 如图是由一些大小相同的小立方块搭成的几何体.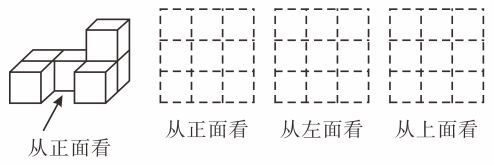 (1)、图中共有个小立方块;(2)、请在下面方格纸中分别画出从正面、左面、上面看到的这个几何体的形状图.27. 如图,在平面直角坐标系中,直线与x,y轴分别相交于A,B,与反比例函数的图象相交于点C,已知 , 点C的横坐标为2.
(1)、图中共有个小立方块;(2)、请在下面方格纸中分别画出从正面、左面、上面看到的这个几何体的形状图.27. 如图,在平面直角坐标系中,直线与x,y轴分别相交于A,B,与反比例函数的图象相交于点C,已知 , 点C的横坐标为2.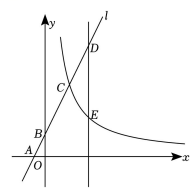 (1)、求k,m的值;(2)、平行于y轴的动直线与l和反比例函数的图象分别交于点D,E,若以B,D,E,O为顶点的四边形为平行四边形,求点D的坐标.28. 如图,
(1)、求k,m的值;(2)、平行于y轴的动直线与l和反比例函数的图象分别交于点D,E,若以B,D,E,O为顶点的四边形为平行四边形,求点D的坐标.28. 如图,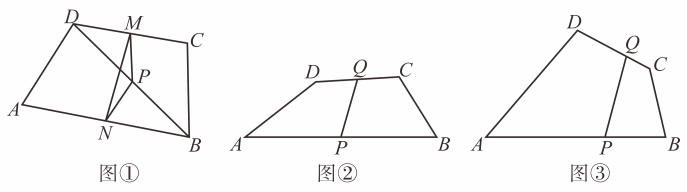 (1)、如图,在四边形中, , P是对角线的中点,M是的中点,N是的中点.求证: . 结合图①,写出完整的证明过程:(2)、如图②,在四边形中, , , , 点P、Q分别为、的中点,求的长。(3)、方法拓展:如图③,在四边形中, , , , 点P、Q分别在、边上, , , 则 . (不用写过程。直接写结果)
(1)、如图,在四边形中, , P是对角线的中点,M是的中点,N是的中点.求证: . 结合图①,写出完整的证明过程:(2)、如图②,在四边形中, , , , 点P、Q分别为、的中点,求的长。(3)、方法拓展:如图③,在四边形中, , , , 点P、Q分别在、边上, , , 则 . (不用写过程。直接写结果)