辽宁省本溪市2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-09-07 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共30分）

1. 分解因式 $4 x^{2} - y^{2}$ 的结果是（）

A、 $(4 x + y) (4 x - y)$ B、 $4 (x + y) (x - y)$ C、 $(2 x + y) (2 x - y)$ D、 $2 (x + y) (x - y)$

查看试题解析
2. 如所示图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在数轴上表示不等式组 ${\begin{array}{l} 1 + x > 0 \\ 2 x - 4 \leq 0 \end{array}$ 的解集，正确的是（）

A、 B、 C、 D、

查看试题解析
4. 在四边形 $A B C D$ 中， $∠ A$ ， $∠ B$ ， $∠ C$ ， $∠ D$ 的度数之比为 $2$ ： $3$ ： $4$ ： $3$ ，则 $∠ D$ 等于（）

A、 $60 °$ B、 $75 °$ C、 $90 °$ D、 $120 °$

查看试题解析
5. 如果 $a > b$ ， $c < 0$ ，那么下列不等式成立的是 $($ 　　 $)$

A、 $a + c > b$ B、 $a + c > b - c$ C、 $a c - 1 > b c - 1$ D、 $a (c - 1) < b (c - 1)$

查看试题解析
6. 下列说法错误的是（）

A、对角分别相等的四边形是平行四边形 B、对角线互相平分的四边形是平行四边形 C、一组对边平行，另一组对边相等的四边形是平行四边形 D、相邻的角互补的四边形是平行四边形

查看试题解析
7. 如果等腰三角形的两边长是6cm和3cm，那么它的周长是（）

A、9cm B、12cm C、12cm或15cm D、15cm

查看试题解析
8. 若函数 $y = k x + b$ 的图象如图所示，则关于 $x$ 的不等式 $k x + 2 b < 0$ 的解集为（）

A、 $x < 3$ B、 $x > 3$ C、 $x < 6$ D、 $x > 6$

查看试题解析
9. 如图，将一副直角三角板按图中所示位置摆放，保持两条斜边互相平行，则 $∠ 1 =$ （）

A、 $30 °$ B、 $25 °$ C、 $20 °$ D、 $15 °$

查看试题解析
10. 如图 $①$ ，在平行四边形 $A B C D$ 中， $A D = 9 c m$ ，动点 $P$ 从 $A$ 点出发，以 $1 c m / s$ 的速度沿着 $A \to B \to C \to A$ 的方向移动，直到点 $P$ 到达点 $A$ 后才停止 $.$ 已知 $△ P A D$ 的面积 $y ($ 单位： $c m^{2})$ 与点 $P$ 移动的时间 $x ($ 单位： $s)$ 之间的函数关系如图 $②$ 所示，图 $②$ 中 $a$ 与 $b$ 分别为（）

A、 $17$ ， $34$ B、 $17$ ， $32$ C、 $19$ ， $36$ D、 $19$ ， $32$

查看试题解析

二、非选择题（70分）

11. 分解因式： $a^{3} - 9 a b^{2}$ =.

查看试题解析
12.
在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，且BE=3，若平行四边形ABCD的周长是16，则EC等于．

查看试题解析
13. 如图，直线 $y = k x + b$ 与直线 $y = m x + n$ 分别与 $x$ 轴交于点 $(- 1 ， 0)$ 、 $(3 ， 0)$ ，则不等式 $(k x + b) (m x + n) > 0$ 的解集为

查看试题解析
14. 当 $- 1 < x < 0$ 时， $x$ ， $\frac{1}{x}$ ， $x^{2}$ 的大小顺序是．

查看试题解析
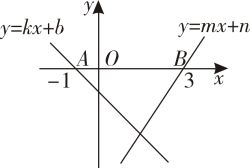15. 某服装厂准备加工400套运动装，在加工完160套后，采用了新技术，使得工作效率比原计划提高了20%，结果共用了18天完成任务，问计划每天加工服装多少套？在这个问题中，设计划每天加工x套，则根据题意可得方程为。

查看试题解析
16. 若 $a = 2023$ ， $b = 2022$ ，则计算 $\frac{1}{2} \times a^{2} - \frac{1}{2} \times b^{2}$ 的结果为．

查看试题解析
17. 如图，正五边形 $A B C D E$ ，则 $∠ A C D$ 的度数为．

查看试题解析
18. 如图，平行四边形 $O A B C$ 的一边在坐标轴上，点 $B$ 的坐标为 $(6 ， 2)$ ，直线 $M N$ ： $y = k x + b$ 把平行四边形的面积分成相等的两部分，且与 $x$ 轴交于点 $(6 ， 0)$ ，则 $k$ 值为．

查看试题解析
19. 解不等式： $5 (x - 2) - 2 (x + 1) > 3$ ．

查看试题解析
20. 先化简再选取一个合适的 $a$ 值代入求值： $(1 - \frac{2}{a + 1}) \div \frac{a^{2} - 2 a + 1}{a^{2} + a}$ ，其中 $a$ 是满足不等式 $2 a - 1 \geq 0$ 解集的一个整数．

查看试题解析
21. 一次函数 $y = (2 a + 4) x - (3 - b)$ ，当 $a$ 、 $b$ 为何值时

(1)、 $y$ 随 $x$ 的增大而增大；

(2)、图象与 $y$ 轴交在 $x$ 轴上方；

(3)、图象过原点．

查看试题解析
22. 如图， $E$ ， $F$ 是四边形 $A B C D$ 的对角线 $A C$ 上两点， $A F = C E$ ， $D F = B E$ ， $D F / / B E .$ 求证：四边形 $A B C D$ 是平行四边形．

查看试题解析
23. 某单位计划 $10$ 月份组织员工到外地旅游，估计人数在 $6 ～ 15$ 人之间．甲、乙量旅行社的服务质量相同，且对外报价都是 $200$ 元 $/$ 人，该单位联系时，甲旅行社表示可给予每位游客 $8$ 折优惠；乙旅行社表示，可先免去一位游客的旅游费用，其余游客 $9$ 折优惠．

(1)、分别写出两旅行社所报旅游费用 $y$ 与人数 $x$ 的函数关系式．

(2)、人数为多少时选择两家旅行社价格都一样？

(3)、当人数在什么范围内应选择乙旅行社？

查看试题解析
24. 平面直角坐标系中，已知 $A (8 ， 0)$ ， $△ A O P$ 为等腰三角形且面积为 $16$ ，求满足条件的 $P$ 点坐标．

查看试题解析
25. 近年来，雾霾天气给人们的生活带来很大影响，空气质量问题倍受人们关注．某单位计划在室内安装空气净化装置，需购进 $A$ ， $B$ 两种设备．每台 $B$ 种设备比每台 $A$ 种设备价格多 $0.7$ 万元，花 $3$ 万元购买 $A$ 种设备和花 $7.2$ 万元购买 $B$ 种设备的数量相同．

(1)、求 $A$ ， $B$ 两种设备每台各多少万元．

(2)、根据单位实际情况，需购进 $A$ ， $B$ 两种设备共 $20$ 台，总费用不高于 $15$ 万元．求 $A$ 种设备至少要购买多少台．

查看试题解析
26. 两个等腰三角形 $△ A B C$ ， $△ A D P$ ， $A B = A C$ ， $A D = A P$ ， $∠ D A P = ∠ B A C$ ，其中 $P$ 在边 $B C$ 所在的直线上 $.$ 连接 $C D$ ．

(1)、问题一：当 $∠ B A C = 90 °$ ，且点 $P$ 在线段 $B C$ 上移动时，则 $∠ B A C$ ， $∠ B C D$ 之间有怎样的数量关系？请说明理由；

(2)、问题二：当 $0 ° < ∠ B A C < 180 °$ ，且点 $P$ 还在线段 $B C$ 上移动，此时 $∠ B A C$ ， $∠ B C D$ 之间有怎样的数量关系？请说明理由；
随着探究的深入，得出一些基本的结论：当点 $P$ 在直线 $B C$ 上移动，所处的位置不同， $∠ B A C$ ， $∠ B C D$ 可能的数量关系是什么？ $($ 直接写出数量关系即可 $)$ ．

查看试题解析