江苏省南京地区2023-2024学年九年级上册苏科版数学开学考试试卷
试卷更新日期:2023-09-07 类型:开学考试
一、选择题(本题共6小题,每小题2分,共12分)
-
1. 围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.如图为某对战局部棋谱,由黑白棋子摆成的图案是中心对称的是( )A、
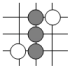 B、
B、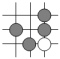 C、
C、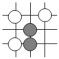 D、
D、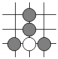 2. 下列方程是一元二次方程的是( )A、 B、 C、 D、3. 将分式 中的m、n都扩大为原来的3倍,则分式的值( )A、不变 B、扩大3倍 C、扩大6倍 D、扩大9倍4. 下列式子中,与是同类二次根式的是( )A、 B、 C、 D、5. 已知a,b是两个连续整数, ,则a,b分别是( )A、 B、 C、0,1 D、1,26. 将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( )
2. 下列方程是一元二次方程的是( )A、 B、 C、 D、3. 将分式 中的m、n都扩大为原来的3倍,则分式的值( )A、不变 B、扩大3倍 C、扩大6倍 D、扩大9倍4. 下列式子中,与是同类二次根式的是( )A、 B、 C、 D、5. 已知a,b是两个连续整数, ,则a,b分别是( )A、 B、 C、0,1 D、1,26. 将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( )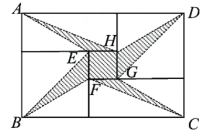 A、正方形纸片的面积 B、四边形EFGH的面积 C、△BEF的面积 D、△AEH的面积
A、正方形纸片的面积 B、四边形EFGH的面积 C、△BEF的面积 D、△AEH的面积二、填空题(本题共10题,每小题2分,共20分)
-
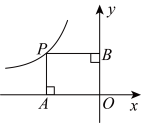
7. 为了了解“双减”背景下全国中小学生完成课后作业的时间情况,比较适合的调查方式是(填“全面调查”或“抽样调查”).8. 一个不透明的袋里装有除颜色外其他完全相同的10个小球,其中有6个黄球,3个白球,1个黑球,将袋中的球摇匀,从中任意摸出一个球,摸出球的可能性最大.9. 两位同学分别说出了某个分式的一些特点,甲同学:这个分式只含有字母;乙同学:当时,分式的值为0.请你写出满足上述全部特点的一个分式 .10. 已知关于的一元二次方程有两个相等的实数根,则m的值为 .11. 如图,在平面直角坐标系中,点是反比例函数图象上的一点,分别过点作轴于点 , 轴于点 , 若四边形的面积为5,则的值是 .
 12. 已知则的值是 .13. 已知 , 则 .14. 如图,一次函数与反比例函数图象交于两点,当时,x的取值范围是 .
12. 已知则的值是 .13. 已知 , 则 .14. 如图,一次函数与反比例函数图象交于两点,当时,x的取值范围是 .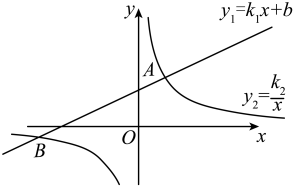 15. 某汽车测评机构对A款电动汽车与B款燃油汽车进行对比调查,发现A款电动汽车平均每公里充电费用比B款燃油车平均每公里燃油费用少0.6元.当充电费和燃油费用均为200元时,A款电动汽车的行驶里程是B款燃油车的4倍.则A款电动汽车平均每公里充电费用为元.16. 如图,在菱形中,点 , 分别在 , 上,沿翻折后,点落在边上的处.若 , , , 则的长为 .
15. 某汽车测评机构对A款电动汽车与B款燃油汽车进行对比调查,发现A款电动汽车平均每公里充电费用比B款燃油车平均每公里燃油费用少0.6元.当充电费和燃油费用均为200元时,A款电动汽车的行驶里程是B款燃油车的4倍.则A款电动汽车平均每公里充电费用为元.16. 如图,在菱形中,点 , 分别在 , 上,沿翻折后,点落在边上的处.若 , , , 则的长为 .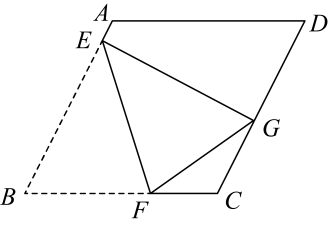
三、解答题(本大题共11小题,共88分)
-
17. 计算:(1)、;(2)、 .18. 解方程:(1)、x2-2x-5=0.(2)、 .19. 化简求值: , 其中 .20. 近年来,随着人们健康睡眠的意识不断提高,社会各界对于初中生的睡眠时间是否充足越发关注.近日我市某学校从全校1200人中随机抽取了部分同学,调查他们平均每日睡眠时间,将得到的数据整理后绘制了如图所示的扇形统计图和频数分布直方图:
 (1)、本次接受调查人数为;图中a=;b=;c=.(2)、教育部《关于进一步加强中小学生睡眠管理工作的通知》文件指出,初中生睡眠时间应达到9小时,试估算该校学生睡眠时间达标人数.21. 在▱ABCD中,
(1)、本次接受调查人数为;图中a=;b=;c=.(2)、教育部《关于进一步加强中小学生睡眠管理工作的通知》文件指出,初中生睡眠时间应达到9小时,试估算该校学生睡眠时间达标人数.21. 在▱ABCD中,
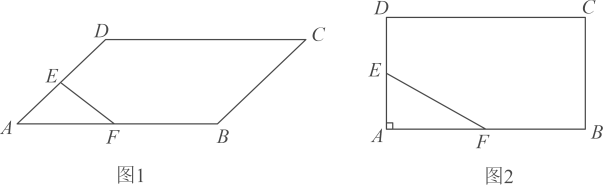 (1)、若 , 如图1,点、分别是边、的中点, , , 求的长;(2)、若 , 如图2,点、分别是边、的中点,请仅用无刻度的直尺在图2中画一个以为边的菱形 . (不写作法,保留作图痕迹,标明字母)22. 端午节前夕,某超市从厂家分两次购进蛋黄粽子、红豆粽子,两次进货时,两种粽子的进价不变.第一次购进蛋黄粽子60袋和红豆粽子90袋,总费用为4800元;第二次购进蛋黄粽子40袋和红豆粽子80袋,总费用为3600元.(1)、求蛋黄粽子、红豆粽子每袋的进价各是多少元?(2)、当蛋黄粽子销售价为每袋70元时;每天可售出20袋,为了促销,该超市决定对蛋黄粽子进行降价销售.经市场调研,若每袋的销售价每降低1元,则每天的销售量将增加5袋.当蛋黄粽子每袋的销售价为多少元时,每天售出蛋黄粽子所获得的利润为220元?23. 如图,一次函数的图象与反比例函数的图象交于 , 两点,且一次函数的图象交轴于点 , 交轴于点 .
(1)、若 , 如图1,点、分别是边、的中点, , , 求的长;(2)、若 , 如图2,点、分别是边、的中点,请仅用无刻度的直尺在图2中画一个以为边的菱形 . (不写作法,保留作图痕迹,标明字母)22. 端午节前夕,某超市从厂家分两次购进蛋黄粽子、红豆粽子,两次进货时,两种粽子的进价不变.第一次购进蛋黄粽子60袋和红豆粽子90袋,总费用为4800元;第二次购进蛋黄粽子40袋和红豆粽子80袋,总费用为3600元.(1)、求蛋黄粽子、红豆粽子每袋的进价各是多少元?(2)、当蛋黄粽子销售价为每袋70元时;每天可售出20袋,为了促销,该超市决定对蛋黄粽子进行降价销售.经市场调研,若每袋的销售价每降低1元,则每天的销售量将增加5袋.当蛋黄粽子每袋的销售价为多少元时,每天售出蛋黄粽子所获得的利润为220元?23. 如图,一次函数的图象与反比例函数的图象交于 , 两点,且一次函数的图象交轴于点 , 交轴于点 .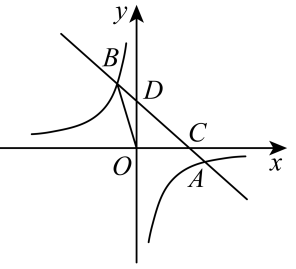 (1)、求一次函数和反比例函数的解析式;(2)、在第四象限的反比例图象上有一点 , 使得 , 请求出点的坐标.24. 先阅读材料,然后回答问题:
(1)、求一次函数和反比例函数的解析式;(2)、在第四象限的反比例图象上有一点 , 使得 , 请求出点的坐标.24. 先阅读材料,然后回答问题:形如的化简,只要找到两个正数、 , 使 , ,
使得 , ,
那么则有 , 例如:化简 , .
 (1)、请根据你从上述材料中得到的启发,化简:;;(2)、在中, , , 其中边的垂直平分线分别交、于点、 , 当时,求的长.(结果要化为最简形式)25. 如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,一元二次方程x2-6x+8=0的两个根是x1=2和x2=4,则方程x2-6x+8=0是“倍根方程”.(1)、根据上述定义,一元二次方程2x2+x-1=0(填“是”或“不是”)“倍根方程”.(2)、若一元二次方程x2-3x+c=0是“倍根方程”,则c= .(3)、若关于x的一元二次方程ax2+bx+c=0(a≠0)是“倍根方程”,则a、b、c之间的关系为 .(4)、若(x-2)(mx-n)=0(m≠0)是“倍根方程”,求代数式4m2-5mn+n2的值.26. 如图,将四边形绕点旋转,使得点的对应点恰好落在射线上,旋转后的四边形为 , 连接交于点 .
(1)、请根据你从上述材料中得到的启发,化简:;;(2)、在中, , , 其中边的垂直平分线分别交、于点、 , 当时,求的长.(结果要化为最简形式)25. 如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,一元二次方程x2-6x+8=0的两个根是x1=2和x2=4,则方程x2-6x+8=0是“倍根方程”.(1)、根据上述定义,一元二次方程2x2+x-1=0(填“是”或“不是”)“倍根方程”.(2)、若一元二次方程x2-3x+c=0是“倍根方程”,则c= .(3)、若关于x的一元二次方程ax2+bx+c=0(a≠0)是“倍根方程”,则a、b、c之间的关系为 .(4)、若(x-2)(mx-n)=0(m≠0)是“倍根方程”,求代数式4m2-5mn+n2的值.26. 如图,将四边形绕点旋转,使得点的对应点恰好落在射线上,旋转后的四边形为 , 连接交于点 .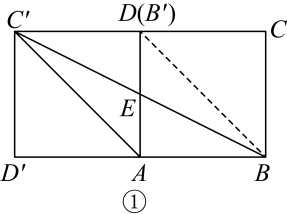
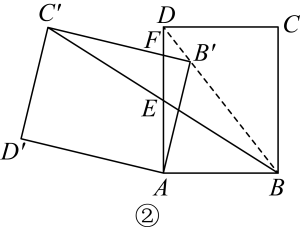
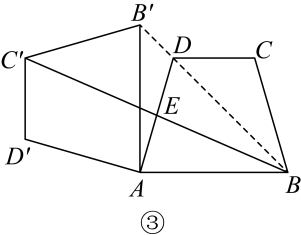 (1)、如图①,若四边形为正方形,则四边形是 . (填序号)
(1)、如图①,若四边形为正方形,则四边形是 . (填序号)①平行四边形;②矩形;③菱形;
(2)、如图②,若四边形为矩形,①求证;
②若 , , 交于点 , 则的长为 ▲ ;
(3)、如图③,若与互相平分,求证 .27. 如图,一次函数y=﹣x+b与反比例函数y= (k≠0)的图象相交于A(﹣1,4)、B(4,﹣1)两点,直线l⊥x轴于点E(﹣4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC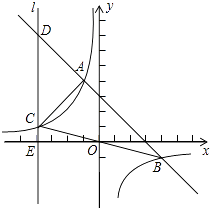 (1)、求出b和k;(2)、求证:△ACD是等腰直角三角形;(3)、在y轴上是否存在点P,使S△PBC=S△ABC?若存在,请求出P的坐标;若不存在,请说明理由.
(1)、求出b和k;(2)、求证:△ACD是等腰直角三角形;(3)、在y轴上是否存在点P,使S△PBC=S△ABC?若存在,请求出P的坐标;若不存在,请说明理由.