河南省信阳市淮滨县2023-2024学年八年级上册数学入学考试试卷

试卷更新日期：2023-09-07 类型：开学考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 在 $0$ 、 $\frac{1}{3}$ 、 $- 1$ 、 $\sqrt{2}$ 这四个数中，最小的数是（）

A、 $0$ B、 $\frac{1}{3}$ C、 $- 1$ D、 $\sqrt{2}$

查看试题解析
2. 在平面直角坐标系中，点 $A (2 ， - 3)$ 在第象限．（）

A、一 B、二 C、三 D、四

查看试题解析
3. 下列调查中，适宜采用全面调查方式的是（）

A、了解一批圆珠笔的使用寿命 B、了解全国七年级学生的身高情况 C、考察人们保护海洋的意识 D、检查一枚用于发射卫星的运载火箭的各零部件

查看试题解析
4. 如图，直线 $a / / b$ ，且直线 $a$ ， $b$ 被直线 $c$ ， $d$ 所截，则下列条件不能判定直线 $c / / d$ 的是（）

A、 $∠ 3 = ∠ 4$ B、 $∠ 1 + ∠ 5 = 180 °$ C、 $∠ 1 = ∠ 2$ D、 $∠ 1 = ∠ 4$

查看试题解析
5. 下列命题中，是假命题的是（）

A、邻补角一定互补 B、平移不改变图形的形状和大小 C、两条直线被第三条直线所截，同位角相等 D、相等的角不一定是对顶角

查看试题解析
6. 已知 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是方程组 ${\begin{array}{l} a x + b y = 5 \\ b x + a y = 1 \end{array}$ 的解，则 $a - b$ 的值是（）

A、 $- 1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
7. 与 $3 + \sqrt{24}$ 最接近的整数是（）

A、 $6$ B、 $7$ C、 $8$ D、 $9$

查看试题解析
8. 已知a，b，c，d是实数，若 $a > b$ ， $c = d$ ，则（）

A、 $a + c > b + d$ B、 $a + b > c + d$ C、 $a + c > b - d$ D、 $a + b > c - d$

查看试题解析
9. 某次数学测验，抽取部分同学的成绩（得分为整数）整理制成频数分布直方图，如图所示．根据图示信息，下列描述不正确的是（）

A、共抽取了50人 B、90分以上的有12人 C、80分以上的所占的百分比是60% D、60.5～70.5分这一分数段的频数是12

查看试题解析
10. 不等式组 ${\begin{matrix} \frac{x - 1}{3} - \frac{1}{2} x < - 1 \\ 4 (x - 1) \leq 2 (x - a) \end{matrix}$ 有3个整数解，则 $a$ 的取值范围是（）

A、 $- 6 \leq a < - 5$ B、 $- 6 < a \leq - 5$ C、 $- 6 < a < - 5$ D、 $- 6 \leq a \leq - 5$

查看试题解析

二、填空题（本大题共8小题，共24.0分）

11. 如图，在正方形网格中， $△ D E F$ 是由 $△ A B C$ 平移得到的 $.$ 则点 $C$ 移动了格 $.$

查看试题解析
12. 满足不等式组 ${\begin{array}{l} 2 x - 5 \leq 0 \\ x - 1 > 0 \end{array}$ 的整数解是．

查看试题解析
13. 某工厂一共有 $1200$ 人，为选拔人才，提出了一些选拔的条件，并进行了抽样调查 $.$ 从中抽出 $400$ 人，发现有 $300$ 人是符合条件的，那么该工厂 $1200$ 人中符合选拔条件的人数约为．

查看试题解析
14. 比较大小： $\frac{\sqrt{5} - 1}{5}$ $\frac{1}{5} . ($ 填“ $>$ ”“ $<$ ”或“ $=$ ” $)$

查看试题解析
15. 计算： $\sqrt{\frac{1}{4}} + \sqrt{0.01} - | \sqrt[3]{- 8} | =$ ．

查看试题解析
16. 如图，已知 $A E // B C$ ， $∠ B A C = 100 °$ ， $∠ D A E = 50 °$ ，则 $∠ C =$ .

查看试题解析
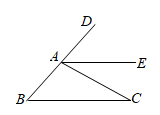17. 已知 $A$ ， $B$ 两件服装的成本共 $500$ 元，鑫洋服装店老板分别以 $30 %$ 和 $20 %$ 的利润率定价后进行销售，该服装店共获利 $130$ 元，则 $A$ 的成本是元， $B$ 的成本是元 $.$

查看试题解析
18. 在平面内取一个定点 $O$ ，叫极点，引一条射线 $O x$ ，叫做极轴，再选定一个长度单位和角度的正方向 $($ 通常取逆时针方向 $) .$ 对于平面内任何一点 $M$ ，用 $ρ$ 表示线段 $O M$ 的长度， $θ$ 表示从 $O x$ 到 $O M$ 的角度， $ρ$ 叫做点 $M$ 的极径， $θ$ 叫做点 $M$ 的极角，有序数对 $(ρ ， θ)$ 就叫点 $M$ 的极坐标，若 $O N ⊥ O X$ ，且点 $N$ 到极点 $O$ 的距离为 $4$ 个单位长度，则点 $N$ 的极坐标可表示为．

查看试题解析

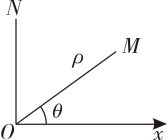
三、解答题（本大题共7小题，共66.0分。解答应写出文字说明，证明过程或演算步骤）

19. 解不等式 $2 x - 1 > \frac{3 x - 1}{2}$ ，并把它的解集在数轴上表示出来.

查看试题解析
20. 已知： $(2 x + 5 y + 4)^{2} + | 3 x - 4 y - 17 | = 0$ ，求 $\sqrt{4 x - 2 y}$ 的平方根．

查看试题解析
21. 如图，BD平分∠ABC，F在AB上，G在AC上，FC与BD相交于点H，∠GFH＋∠BHC＝180°.求证∠1＝∠2.

查看试题解析

22. 双减政策实施后，学校为了解八年级学生每日完成书面作业所需时长

x (

单位：小时

)

的情况，在全校范围内随机抽取了八年级若干名学生进行调查，并将所收集的数据分组整理，绘制了如下两幅不完整的统计图表，请根据图表信息解答下列问题．

八年级学生每日完成书面作业所需时长情况的统计表

组别	所需时长 $($ 小时 $)$	学生人数 $($ 人 $)$
$A$	$0 < x \leq 0.5$	$15$
$B$	$0.5 < x \leq 1$	$m$
$C$	$1 < x \leq 1.5$	$n$
$D$	$1.5 < x \leq 2$	$5$

(1)、求统计表中

m

，

n

的值．

(2)、已知该校八年级学生有

800

人，试估计该校八年级学生中每日完成书面作业所需时长满足

0.5 < x \leq 1.5

的共有多少人．

查看试题解析

23. 如图，在平面直角坐标系中，已知点 $A (- 3 ， 3)$ 、 $B (- 5 ， 1)$ 、 $C (- 2 ， 0)$ 、 $P (a ， b)$ 是三角形 $A B C$ 的边 $A C$ 上任意一点，三角形 $A B C$ 经过平移后得到三角形 $A_{1} B_{1} C_{1}$ ，点 $A$ 、 $B$ 、 $C$ 的对应点分别为 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ ，点 $P$ 的对应点为 $P_{1} (a + 6 ， b - 2)$ ．
⑴直接写出点 $C_{1}$ 的坐标；
⑵在图中画出三角形 $A_{1} B_{1} C_{1}$ ；
⑶求三角形 $A O A_{1}$ 的面积．

查看试题解析
24. 2022年2月4日至20日冬季奥运会在北京举行.某商店特购进冬奥会纪念品“冰墩墩”摆件和挂件共180个进行销售.已知“冰墩墩”摆件的进价为80元/个，“冰墩墩”挂件的进价为50元/个.

(1)、若购进“冰墩墩”摆件和挂件共花费了11400元，请分别求出购进“冰墩墩”摆件和挂件的数量.

(2)、该商店计划将“冰墩墩”摆件售价定为100元/个，“冰墩墩”挂件售价定为60元/个，若购进的180个“冰墩墩”摆件和挂件全部售完，且至少盈利2900元，求购进的“冰墩墩”挂件不能超过多少个？

查看试题解析
25. 如图 $①$ ，已知直线 $l_{1} / / l_{2}$ ，且 $l_{3}$ 和 $l_{1}$ ， $l_{2}$ 分别交于 $A$ ， $B$ 两点， $l_{4}$ 和 $l_{1}$ ， $l_{2}$ 分别交于 $C$ ， $D$ 两点，点 $P$ 在线段 $A B$ 上， $∠ A C P = ∠ 1$ ， $∠ B D P = ∠ 2$ ， $∠ C P D = ∠ 3$ ．

(1)、若 $∠ 1 = 22 °$ ， $∠ 2 = 33 °$ ，则 $∠ 3 =$ ．

(2)、试找出 $∠ 1$ ， $∠ 2$ ， $∠ 3$ 之间的数量关系，并说明理由．

(3)、应用(2)中的结论解答下面的问题：
如图 $②$ ，点 $A$ 在 $B$ 的北偏东 $40 °$ 的方向上，在 $C$ 的北偏西 $45 °$ 的方向上，求 $∠ B A C$ 的度数．

(4)、如果点 $P$ 在直线 $l_{3}$ 上且在线段 $A B$ 外侧运动 $($ 点 $P$ 和 $A$ ， $B$ 两点不重合 $)$ ，其他条件不变，试探究 $∠ 1$ ， $∠ 2$ ， $∠ 3$ 之间的关系．

查看试题解析